Файл: 7.3. Пример решения задачи нелинейного программирования.docx
ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 882
Скачиваний: 17
Пример решения задачи нелинейного программирования
Тема: Нелинейное программирование. Применение основной теоремы выпуклого анализа Куна – Таккера.
Задание. По плану производства необходимо изготовит количество изделий, указанное в условии каждого задания «общий объём выпуска». Эти изделия могут быть изготовлены двумя технологическими способами. Стало известно, что при производстве х1 изделий первым способом затраты определяются функцией двух переменных х1, х2, соответствующей каждому варианту. При изготовлении х2 изделий вторым способом затраты также определяются функцией двух переменных х1, х2, соответствующей каждому варианту.
Определить оптимальное число изделий, изготовленных различными способами, так чтобы общие затраты на производство продукции были минимальными (см. варианты заданий). Вычислить получаемую экономию от такого решения задачи.
Затраты для производства первым способом: x12 + 2 x1 руб.
Затраты для производства вторым способом: x22 + 16 x2 руб.
Общий объём выпуска: 100 шт.
Решение:
введём функцию суммарных затрат на
производство
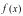 и
сформулируем математическую постановку
задачи:
и
сформулируем математическую постановку
задачи:
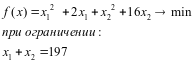
Составляем функцию Лагранжа и задачу условной оптимизации сводим к задаче безусловной оптимизации:
Находим первые частные производные функции Лагранжа и приравниваем их к нулю. Из полученной системы уравнений находим значения переменных х1, х2, возможно, соответствующие оптимальному решению исходной задачи.
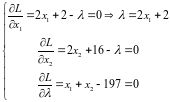
Подставляем выражение через х1 во второе уравнение:
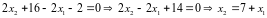 .
.
Полученное выражение для х2 подставляем в третье уравнение:
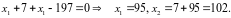
Проверяем,
имеет ли исходная функция
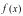 экстремум в точке (95; 102). Для этого
вычисляем вторые частные производные
экстремум в точке (95; 102). Для этого
вычисляем вторые частные производные
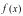 и определитель, составленный из них:
и определитель, составленный из них:
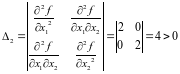 .
Следовательно, по теореме о достаточном
условии существования экстремума
функции нескольких переменных функция
.
Следовательно, по теореме о достаточном
условии существования экстремума
функции нескольких переменных функция
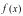 в точке имеет (95; 102) минимум, равный f
(95, 102) = 952 +
295
+ 1022
+ 16102
= 21251.
в точке имеет (95; 102) минимум, равный f
(95, 102) = 952 +
295
+ 1022
+ 16102
= 21251.
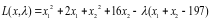 .
.