ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5248
Скачиваний: 10

96
Далее
(
)
2
,
1
≥
Γ
∈
−
∈
∃
∈
∀
⇒
∅
≠
i
при
x
y
i
X
y
i
X
x
i
X
. (5.4)
Действительно
,
пусть
∅
≠
i
X
, a
x
−
произвольная
вершина
из
X
i
.
По
определению
X
i
имеем
j
i
j
j
i
j
X
U
X
x
и
X
U
x
1
1
1
1
\
;
−
=
−
=
∈
⊆
Γ
значит
и
подавно
j
i
j
X
U
X
x
1
1
\
−
=
∈
,
а
так
как
1
−
∉
i
X
x
,
то
j
i
j
X
U
x
2
1
−
=
⊄
Γ
,
следовательно
,
∅
≠
−
∩
Γ
1
i
X
x
,
откуда
и
вытекает
(5.4).
Наконец
,
из
(5.4)
и
из
предположения
об
отсутствии
в
L
ормаршрутов
длины
>
)
(
L
τ
заключаем
,
что
∅
=
⇒
+
>
i
X
L
i
1
)
(
τ
.
(5.5)
На
основании
(5.3), (5.5)
и
не
пустоты
X
имеем
j
l
j
X
X
∪
1
−
=
,
где
1
≤
l
≤
τ
(
L
) +1
значит
,
ввиду
(5.1)
и
(5.2)
система
множеств
… X
X
X
,
,
,
2
1
есть
полная
раскраска
вершин
графа
L
в
l
≤
τ
(
L
) + 1
цветов
.
Отсюда
и
из
(*)
вытекает
справедливость
теоремы
.
Таким
образом
,
нахождении
хроматического
числа
( )
L
γ
рав
-
носильно
нахождению
числа
( )
L
τ
,
а
для
построения
какой
-
либо
из
минимальных
раскрасок
достаточно
задать
одну
из
ориентаций
рёбер
так
,
чтобы
полученный
орграф
L
не
содержал
ормаршру
-
тов
длины
более
( )
L
τ
,
а
затем
выявить
множества
… X
X
X
,
,
,
2
1
,
фигурирующие
во
второй
части
доказательства
.
Пусть
)
(
j
L
i
r
R
R
=
=
−
матрица
смежности
графа
L
над
}
1
,
0
{
B
B
=
;
{ }
ij
ε
−
система
переменных
в
}
1
,
0
{
B
,
соответствую
-
щих
рёбрам
L;
})
{
(
})
({
ij
ij
ij
r
R
R
ε
ε
=
=
−
общий
вид
матрицы
смежности
орграфов
L
,
получаемых
из
L всевозможными
ориен
-
тациями
рёбер
.

97
Как
известно
,
элемент
{ }
ij
ij
r
ε
)
(
матрицы
{ }
( )
[
]
ij
R
ε
равен
1
или
0,
смотря
по
тому
,
существует
или
не
существует
ормаршрут
длины
из
вершины
x
i
в
вершину
x
j
в
орграфе
L
,
полученном
из
L
ориентацией
рёбер
,
которая
отвечает
системе
значений
}
{
ij
ε
.
Поэтому
( )
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
≡
∑
=
=
1
)
(
max
)
(
1
,
ij
L
n
j
i
ij
r
L
ε
τ
,
где
≡
означает
равенство
при
всех
системах
значений
перемен
-
ных
{ }
ij
ε
.
Для
нахождения
одной
из
минимальных
раскрасок
надо
задать
конкретную
систему
значений
{ }
*
ij
ε
,
при
которой
( )
(
)
{ }
,
0
1
*
)
(
1
,
=
∑
+
=
ij
r
n
j
i
ij
r
r
ε
τ
после
чего
образовать
матрицу
{ }
( )
*
ij
R
ε
и
определить
по
ней
множества
… X
X
X
,
,
,
2
1
следующим
образом:
к
1
X
относим
все
те
вершины
X
x
∈
,
которым
в
{ }
( )
*
ij
R
ε
отвечают
строки
из
од
-
них
нулей
;
затем
вычёркиваем
из
матрицы
строки
и
столбцы
,
со
-
ответствующие
вершинам
1
X
по
оставшейся
матрице
ищем
2
X
точно
так
же
,
как
искали
1
X
по
исходной
;
и
так
далее
до
тех
пор
,
пока
не
будет
исчерпана
вся
матрица
.
Существенным
недостатком
этого
способа
является
весьма
быстрый
рост
сложности
булева
выражения
( )
{ }
0
)
(
1
,
=
∑
=
ij
r
n
j
i
ij
r
ε
при
увеличении
.
Пример 5.1.4.
Рассмотрим
граф
,
показанный
на
рис
. 5.1.3.
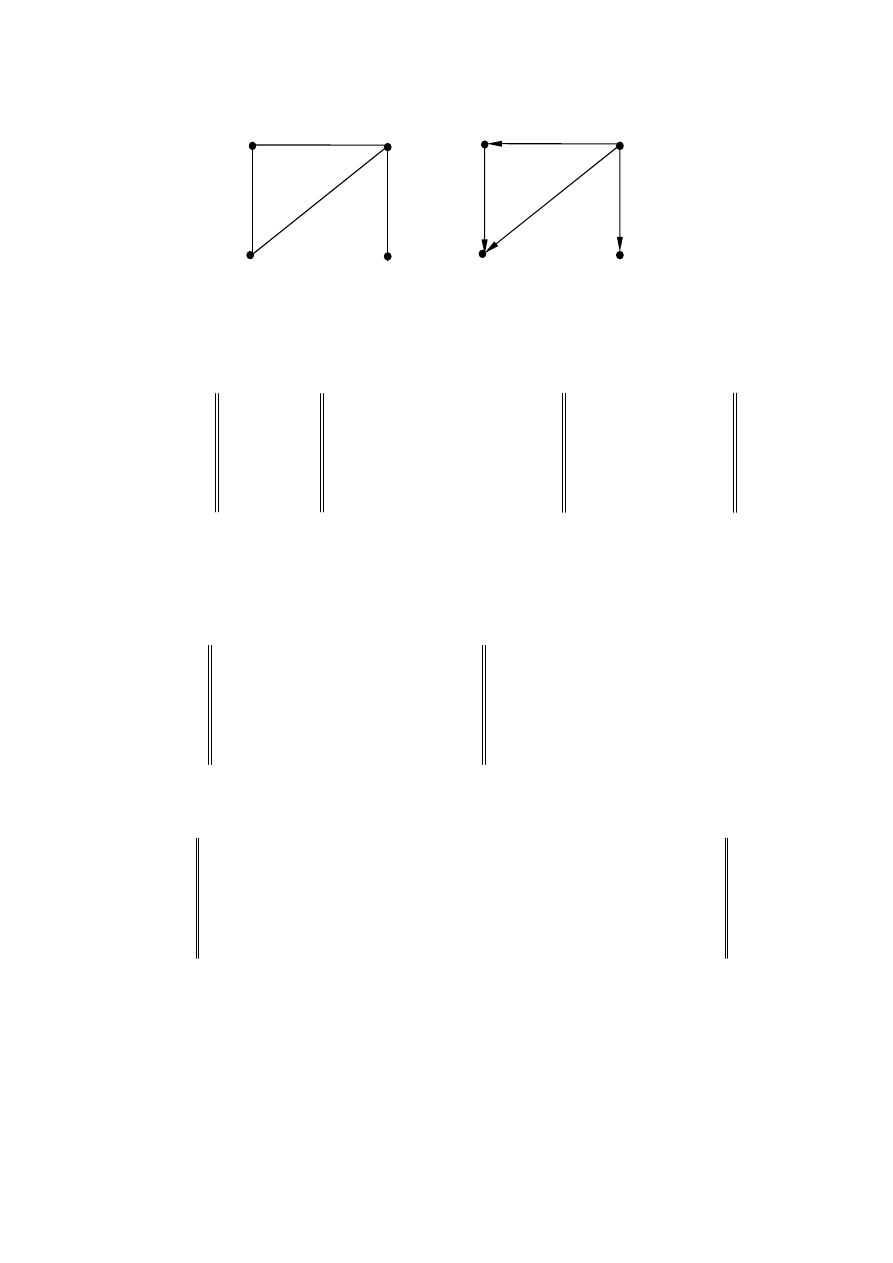
98
Имеем
0
1
0
0
1
0
1
1
0
1
0
1
0
1
1
0
=
R
{ }
( )
0
0
0
0
0
0
0
0
34
34
23
13
23
12
13
12
ε
ε
ε
ε
ε
ε
ε
ε
ε
′
′
′
′
=
ij
R
{ }
1
34
34
23
13
23
12
13
12
1
,
=
+
′
+
′
+
′
+
+
′
+
+
=
∑
=
ε
ε
ε
ε
ε
ε
ε
ε
ε
ij
n
j
i
ij
r
.
Это
означает
,
что
ввиду
непустоты
данного
графа
,
ормар
-
шруты
длины
1
существуют
при
любой
ориентации
рёбер
.
{ }
( )
[
]
0
0
0
0
0
0
34
23
34
13
13
12
23
12
24
23
13
12
13
23
34
13
23
12
23
13
2
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
′
′
′
′
′
′
′
′
′
′
=
ij
R
{ }
1
34
23
34
13
13
12
23
12
34
23
13
12
13
23
34
13
23
12
23
13
1
,
2
≡
′
′
+
′
′
+
′
+
′
′
+
+
′
+
′
+
+
+
′
=
∑
=
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ij
n
j
i
ij
r
{ }
( )
[
]
0
0
0
0
0
0
0
0
0
34
13
12
34
23
12
23
13
12
23
13
12
34
13
12
23
13
12
23
13
12
34
23
12
23
13
12
13
23
12
3
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
′
′
′
′
′
′
′
+
′
′
′
+
′
′
′
′
′
+
′
=
ij
R
{ }
+
′
+
′
+
+
′
′
+
+
′
′
+
′
=
∑
=
23
13
12
34
13
12
23
13
12
23
13
12
34
23
13
23
13
12
13
23
12
1
,
3
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ij
n
j
i
ij
r
1
34
13
12
34
23
13
23
13
12
≠
′
′
+
′
′
′
+
′
′
+
ε
ε
ε
ε
ε
ε
ε
ε
ε
,
2
2
3
3
1
4
1
4
Рис. 5.1.3
Рис. 5.1.4

99
следовательно
,
3
,
2
=
=
γ
τ
.
Одной
из
систем
значений
,
при
которой
последняя
сумма
равна
нулю
,
будет
,
0
23
13
12
=
=
=
ε
ε
ε
.
1
34
=
ε
Соответствующий
орграф
изображён
на
рис
. 5.1.4,
а
его
мат
-
рица
смежности
4
3
2
1
0
0
0
0
1
0
1
1
0
0
0
1
0
0
0
0
=
R
Из
R
сразу
находим
x
1
={1,4},
вычёркивая
первую
и
четвёр
-
тую
строки
,
а
также
первый
и
четвёртый
столбцы
,
получаем
мат
-
рицу
3
2
0
1
0
0
,
из
которой
x
2
= {2},
вычёркивая
первую
строку
и
первый
столбец
,
получаем
,
что
x
3
= {3}.
Таким
образом
, x(L) = 3,
а
одной
из
ми
-
нимальных
раскрасок
вершин
является
такая
,
при
которой
первая
и
четвёртая
вершины
окрашены
в
красный
цвет
,
вторая
−
в
зелё
-
ный
и
третья
−
в
синий
.
5.2
Определение
хроматического
числа
плоского
графа
Пусть
каждой
вершине
X
x
∈
обыкновенного
графа
L=(X,U)
отнесена
некоторая
точка
плоскости
,
каждому
ребру
U
u
∈
пря
-
молинейный
отрезок
с
концами
в
тех
случаях
,
которые
отвечают
вершинам
,
соединённым
с
L
ребром
U. Возникает
вопрос
о
воз
-
можности
изображения
их
в
плоскости
,
чтобы
никакие
два
ребра
не
пересекались
в
точке
,
являющейся
концом
хотя
бы
одного
из
тех
рёбер
.
Пример 5.2.1.
Задача
о
трёх
городах
и
трёх
источниках
снабжения
.
Имеются
три
города
A,B,C
и
три
источника
снабже
-
ния
:
водонапорная
башня
D,
газовый
завод
E,
электростанция
F
(
рис
. 5.2.1).
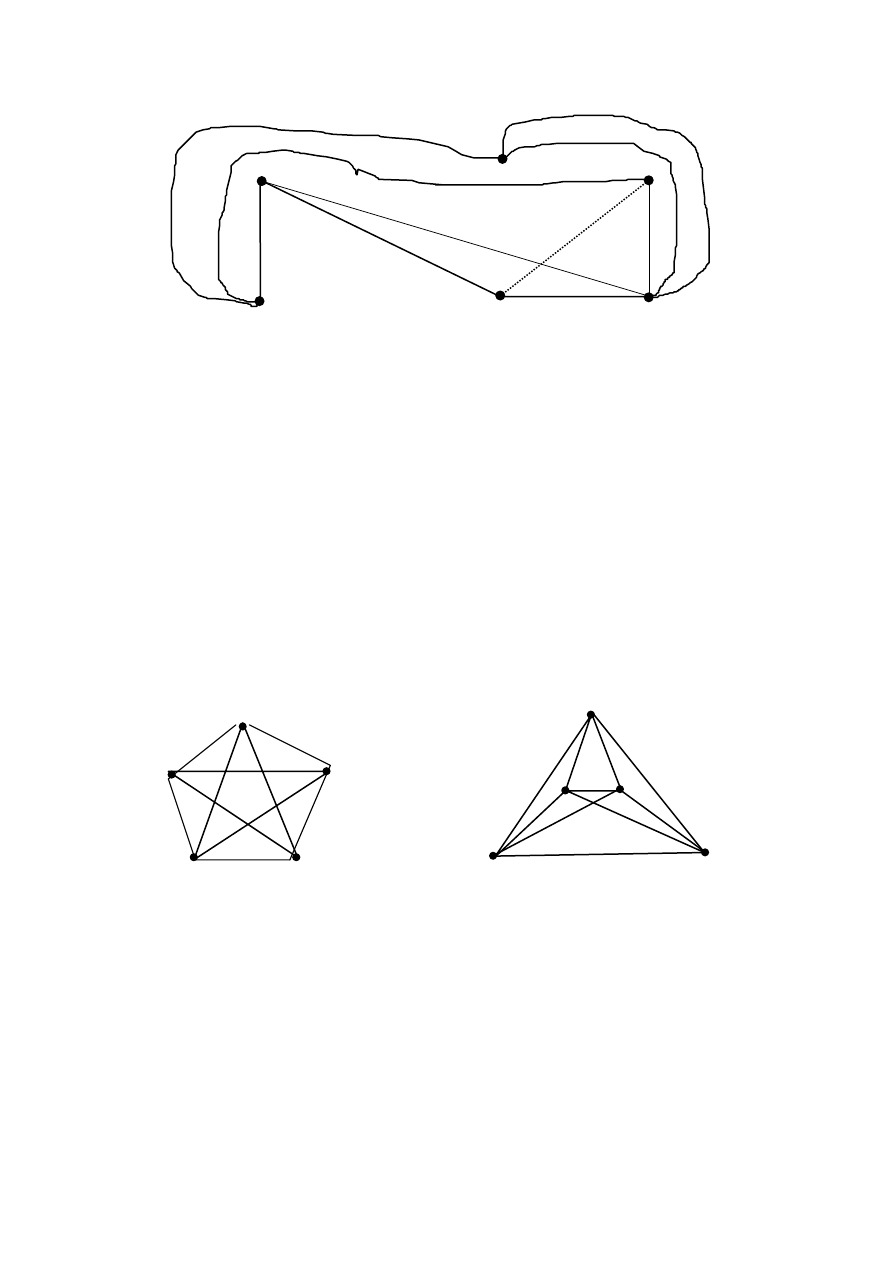
100
Можно
ли
начертить
(
на
плане
)
три
города
,
три
источника
и
все
линии
передач
таким
образом
,
чтобы
никакие
две
линии
не
пересекались
между
собой
в
не
концевых
точках
?
Непосредст
-
венные
попытки
показывают
,
что
всегда
можно
нарисовать
8
ли
-
ний
,
а
девятая
обязательно
пересечёт
хотя
бы
одну
из
этих
вось
-
ми
.
Для
любого
графа
,
однако
,
можно
всегда
попытаться
вы
-
брать
такое
расположение
его
вершин
в
плоскости
,
при
котором
количество
лишних
пересечений
было
бы
наименьшим
;
так
,
граф
F
на
рис
. 5.2.2
допускает
изображение
с
одной
лишней
точкой
пе
-
ресечения
–
рис
. 5.2.3.
В
трёхмерном
пространстве
обыкновенный
граф
всегда
до
-
пускает
такое
расположение
,
при
котором
два
ребра
не
пересека
-
ются
в
точке
,
отличной
от
концевых
.
Граф
называется
плоским
,
если
он
может
быть
расположен
на
плоскости
без
лишних
точек
пересечения
.
Рис. 5.2.1
A
B
C
D
E
F
Рис. 5.2.2
Рис. 5.2.3