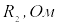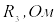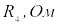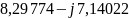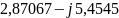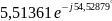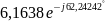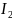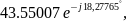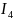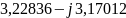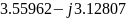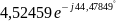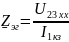Файл: Расчёт разветвлённых линейных электрических цепей однофазного синусоидального тока.docx
Добавлен: 02.02.2019
Просмотров: 773
Скачиваний: 14
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра теоретических основ электротехники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2
По дисциплине «Основы теории цепей»
На тему «Расчёт разветвлённых линейных электрических цепей однофазного синусоидального тока»
Специальность «Информационные системы»
Выполнил Ануарбеков Шыңғыс Группа ИС-16-2
Принял доцент каф. ТОЭ Айтжанов Н.М.
_________ «____»____________2017г.
Алматы 2017
Содержание
Введение...................................................................................................................3
Задание.....................................................................................................................4
Расчетная часть........................................................................................................6
Уравнения по законам Кирхгофа в двух формах.........................................6
Методы контурных токов и узловых потенциалов......................................8
Свод результатов расчетов в таблицу.........................................................13
Метод эквивалентного генератора..............................................................13
Баланс комплексных мощностей................................................................17
Мгновенные значения токов и график тока................................................17
Заключение.............................................................................................................19
Список литературы................................................................................................20
Введение
Цель работы: умение составлять систему уравнения по законам Кирхгофа для разветвлённых электрических цепей однофазного синусоидального тока, рассчитывать токи методом контурных токов, методом узловых потенциалов в комплексной форме, методом эквивалентного генератора.
Дана
электрическая цепь, в которой действуют
источники синусоидальной ЭДС
 и синусоидального тока
и синусоидального тока
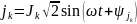 (см. рисунок 2.1-2.10). Действующие значения
ЭДС
(см. рисунок 2.1-2.10). Действующие значения
ЭДС
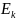 и тока источника тока
и тока источника тока
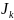 , а также начальные фазы
, а также начальные фазы
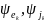 приведены в таблице 2.2. Параметры
электрической цепи приведены в таблицах
2.1, 2.3.
приведены в таблице 2.2. Параметры
электрической цепи приведены в таблицах
2.1, 2.3.
Таблица 2.1
|
Год поступления |
Первая буква фамилии |
|||||||||
|
Четный |
А БВ |
ГДЕ |
ЖЗИ |
КЛ |
МН |
ОПР |
СТ У |
ФХЦ |
ЧШ Щ |
ЭЮ Я |
|
Нечетный |
КЛ |
ОПР |
СТ У |
ФХЦ |
АБ В |
ГД Е |
ЖЗИ |
МН |
ЭЮ Я |
ЧШЩ |
|
№ схемы |
3.1 |
3.2 |
3.3 |
3.4 |
3.5 |
3.6 |
3.7 |
3.8 |
3.9 |
3.10 |
|
|
3 |
10 |
20 |
10 |
40 |
10 |
40 |
20 |
10 |
40 |
|
|
5 |
2 |
30 |
20 |
16 |
20 |
10 |
60 |
20 |
5 |
|
|
8 |
6 |
25 |
5 |
20 |
40 |
30 |
10 |
50 |
12 |
|
|
2 |
16 |
65 |
25 |
15 |
100 |
50 |
40 |
40 |
18 |
|
|
4 |
25 |
20 |
10 |
8 |
10 |
10 |
10 |
30 |
30 |
|
|
10 |
10 |
15 |
30 |
15 |
25 |
40 |
5 |
60 |
40 |
|
|
6 |
5 |
20 |
8 |
5 |
20 |
20 |
18 |
40 |
10 |
|
|
18 |
10 |
30 |
20 |
8 |
50 |
30 |
10 |
20 |
30 |
Таблица 2.2
|
Год поступления |
Последняя цифра студенческого билета |
|||||||||
|
Четный |
0 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
Нечетный |
2 |
5 |
6 |
1 |
3 |
4 |
7 |
8 |
9 |
0 |
|
|
10 |
20 |
15 |
30 |
25 |
16 |
12 |
30 |
40 |
18 |
|
|
20 |
12 |
18 |
28 |
30 |
35 |
40 |
15 |
8 |
25 |
|
|
30 |
15 |
20 |
10 |
16 |
15 |
45 |
50 |
30 |
20 |
|
|
35 |
20 |
15 |
25 |
10 |
18 |
32 |
40 |
42 |
35 |
|
|
10 |
15 |
8 |
5 |
20 |
10 |
6 |
12 |
3 |
4 |
|
|
30 |
40 |
25 |
45 |
-40 |
60 |
0 |
35 |
50 |
70 |
|
|
120 |
80 |
90 |
-30 |
-60 |
-40 |
30 |
-10 |
-20 |
-90 |
|
|
130 |
150 |
180 |
-45 |
-30 |
-60 |
-90 |
40 |
15 |
20 |
|
|
0 |
20 |
90 |
-60 |
-45 |
-50 |
45 |
70 |
30 |
120 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Таблица 2.3
|
Год поступления |
Предпоследняя цифра студенческого билета |
|||||||||
|
Четный |
2 |
3 |
4 |
8 |
0 |
1 |
5 |
7 |
6 |
9 |
|
Нечетный |
8 |
2 |
0 |
7 |
6 |
4 |
3 |
5 |
9 |
1 |
|
|
60 |
100 |
40 |
50 |
80 |
20 |
15 |
25 |
30 |
12 |
|
|
50 |
45 |
90 |
40 |
30 |
25 |
10 |
20 |
18 |
6 |
|
|
6 |
10 |
8 |
15 |
20 |
30 |
25 |
40 |
60 |
10 |
|
|
120 |
100 |
80 |
60 |
40 |
20 |
10 |
8 |
15 |
45 |
|
МЭГ, График тока |
i4 |
i1 |
i2 |
i3 |
i4 |
i1 |
i2 |
i3 |
i4 |
i1 |

Рисунок 2.1
Задание:
1) Записать уравнения по законам Кирхгофа в дифференциальной и комплексной формах.
2) Определить комплексные действующие значения токов во всех ветвях методом контурных токов и методом узловых потенциалов. Свести результаты расчетов в одну таблицу.
3) Определить комплекс действующего значения требуемого тока (см. таблицу 2.3) методом эквивалентного генератора.
4) Проверить баланс комплексных мощностей в цепи.
5)
Записать мгновенные значения токов
всех ветвей и построить график одного
из токов i(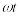 )
(см. таблицу 2.3).
)
(см. таблицу 2.3).
Расчетная часть
1) Записать уравнения по законам Кирхгофа в дифференциальной и комплексной формах.
Законы Кирхгофа в дифференциальной форме. Законы Кирхгофа в дифференциальной форме записываются для мгновенных значений переменных токов и напряжений.

Первый
закон Кирхгофа: алгебраическая сумма
мгновенных значений токов в узле схемы
равна нулю:
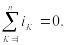 Со знаком «+» записываются токи ік,
положительные направления которых
направлены к рассматриваемому узлу, со
знаком «-» записываются токи
ік,
положительные направления которых
направлены от данного узла (или наоборот).
Число
уравнений, составляемых по первому
закону Кирхгофа, равно
Со знаком «+» записываются токи ік,
положительные направления которых
направлены к рассматриваемому узлу, со
знаком «-» записываются токи
ік,
положительные направления которых
направлены от данного узла (или наоборот).
Число
уравнений, составляемых по первому
закону Кирхгофа, равно
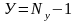 ,
где
,
где
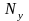 -
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений по I
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3:
-
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений по I
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3:
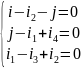
Второй закон Кирхгофа: алгебраическая сумма мгновенных ЭДС всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура:
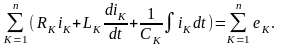
Второй
закон Кирхгофа записывается для
независимых контуров схемы, независимые
контура выбираются так же, как и для
цепей постоянного тока. Со знаком «+»
записываются мгновенные напряжения,
если положительные направления токов
ік
и направление обхода контура совпадают,
в противном случае напряжения записываются
со знаком «-». Мгновенные ЭДС
ек
записываются со знаком «+», если
положительные направления
ек
и направление обхода контура совпадают.
Число уравнений, составляемых по второму
закону Кирхгофа, равно:
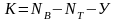 ,
где
,
где
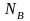 - число ветвей,
- число ветвей,
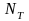 - число источников тока. Исходя из этого,
в цепи (рис 2.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 2.1). И для
каждого контура (внешний контур и контур
2342) запишем уравнение по II
закону Кирхгофа:
- число источников тока. Исходя из этого,
в цепи (рис 2.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 2.1). И для
каждого контура (внешний контур и контур
2342) запишем уравнение по II
закону Кирхгофа:

Общая система уравнений по законам Кирхгофа в дифференциальной форме будет выглядеть следующим образом:

Законы Кирхгофа в комплексной форме.
Для узла электрической цепи переменного тока по первому закону Кирхгофа сумма мгновенных значений токов, направленных к узлу, равна сумме мгновенных значений токов, направленных от узла. То же самое правило справедливо и при записи токов в комплексной форме. Запишем уравнения для 1, 2, 3 узлов:
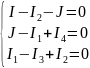
Для замкнутого контура электрической цепи переменного тока по второму закону Кирхгофа алгебраическая сумма мгновенных значений ЭДС, действующих в контуре, равна алгебраической сумме мгновенных значений падений напряжения на отдельных его участках. Приписав ЭДС и токам, совпадающим по направлению с направлением обхода контура, знак плюс, а несовпадающим – минус, получим при комплексной записи для любого замкнутого контура:
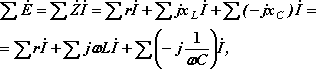
Таким образом, для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений. Выбираем два независимых контура, не имеющих источника тока, затем произвольно выбираем обход контура (рис 2.1). И для каждого контура (внешний контур и контур 2-3-4-2(узлы)) запишем уравнение по II закону Кирхгофа:

Общая система уравнений по законам Кирхгофа в комплексной форме будет выглядеть следующим образом:
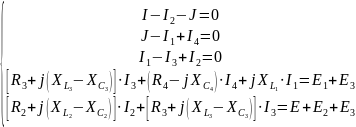
2) Определить комплексные действующие значения токов во всех ветвях методом контурных токов и методом узловых потенциалов. Свести результаты расчетов в одну таблицу.
Сначала необходимо найти общее сопротивление в каждой ветви и действующие значения ЭДС и источника тока:
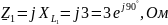
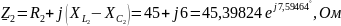
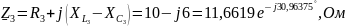
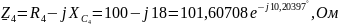
По
данным
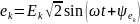 ,
где
,
где
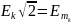
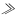
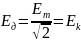 ,
аналогично и для
,
аналогично и для
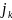 .
.
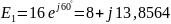 ,
В
,
В
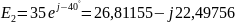 ,
В
,
В
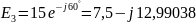 ,
В
,
В
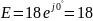 ,
В
,
В
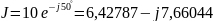 ,
А
,
А
Если
электрическая цепь содержит Nт
идеальных
источников тока, то при составлении
уравнений методом контурных токов
рекомендуется выбирать Nт
контурных токов так, чтобы каждый из
них проходил через один источник тока
(эти контурные совпадают с соответствующими
токами источников тока и задаются
условием задачи). В цепи (рис 2.2.) имеется
1 источник тока. Следовательно, выбираем
один контурный ток, который будет
проходить через имеющийся источник
тока. Оставшиеся К=Nв-Nу+1-Nт
контурных
токов выбирают так, чтобы они проходили
по ветвям, не содержащим источников
тока (К=Nв-Nу+1-Nт-
число неизвестных контурных токов, Nв-
число ветвей, Nу-
число узлов, Nт-число
источников тока). К = 6-4+1-1=2 – число
неизвестных контурных токов. Для
определения оставшихся К контурных
токов составляют K
контурных уравнений по второму закону
Кирхгофа.

Составим систему уравнений по методу контурных токов для разветвленной электрической цепи однофазного синусоидального тока (рис 2.2):

Рисунок 1.2.
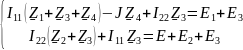
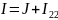
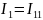
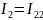
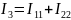
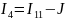 ,
где
,
где
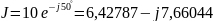 ,
А
,
А
Решение:

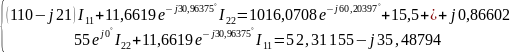

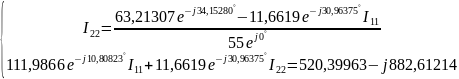
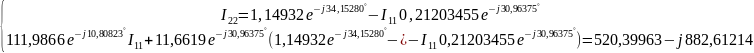
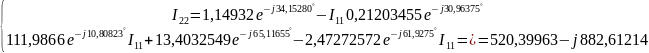
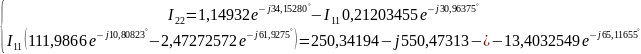
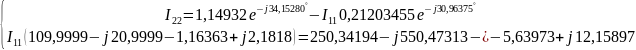
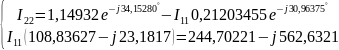
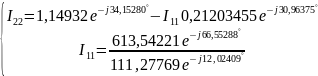

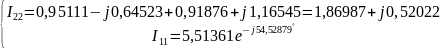
Таким образом,
 ,
A
,
A
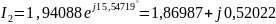 ,
A
,
A
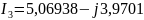 =
=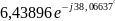 ,
A
,
A
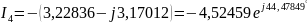 ,
A
,
A
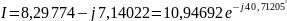 ,
A
,
A
Метод
узловых потенциалов позволяет уменьшить
число уравнений системы до числа
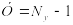 .
Суть
метода
узловых потенциалов заключается в
определении потенциалов узлов
электрической цепи, токи рассчитываются
по закону Ома. При составлении уравнений
по методу узловых потенциалов, потенциал
одного из узлов принимают равным нулю,
для определения потенциалов оставшихся
узлов составляются уравнения.
.
Суть
метода
узловых потенциалов заключается в
определении потенциалов узлов
электрической цепи, токи рассчитываются
по закону Ома. При составлении уравнений
по методу узловых потенциалов, потенциал
одного из узлов принимают равным нулю,
для определения потенциалов оставшихся
узлов составляются уравнения.
Возьмем
узел 4 за базовый и будем считать, что
он равен нулю. Автоматически значение
потенциала в узле 1 становится равным
E.
(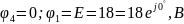 ).
).
Составим систему уравнений по методу узловых потенциалов для разветвленной электрической цепи однофазного синусоидального тока (рис 2.3), так как значения потенциалов в узлах 1 и 4 известны, то нам необходимо составить систему из 2 уравнений для узлов 2 и 3:

Рисунок 2.3
 ,
,
где
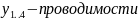 (величина,
обратная сопротивлению).
(величина,
обратная сопротивлению).
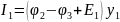
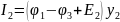
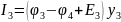

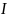 найдем,
применив I
закон Кирхгофа
найдем,
применив I
закон Кирхгофа
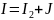
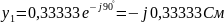
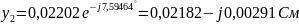

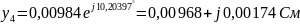
Решение:
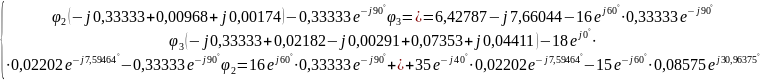
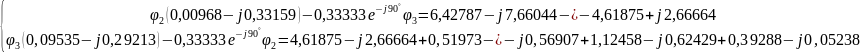

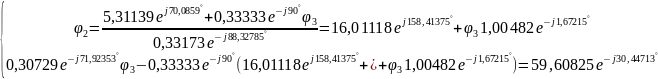

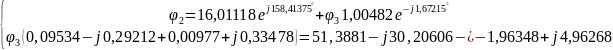
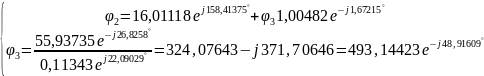

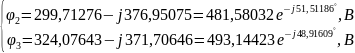
Следовательно,
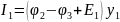 =
=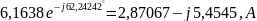
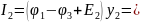
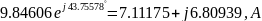
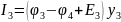 =
=
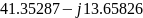 =
=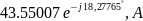
 =
=
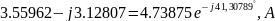
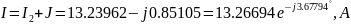
Результаты занесем в таблицу:
|
Токи/Метод |
Метод контурных токов |
Метод узловых потенциалов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как видно из таблицы, значение токов по МУП и МКТ отличаются незначительно, такие отклонения обусловлены неравномерным округлением значений при решении систем уравнений.
3)
Определить
комплекс действующего значения требуемого
тока (см. таблицу 2.3) методом эквивалентного
генератора.
В данном случае необходимо рассчитать
 .
.
При
решении задач по основам теории цепей,
зачастую требуется знать режим работы
не всей цепи, а только одной определённой
ветви. Для определения параметров такой
ветви существует метод
эквивалентного генератора.
Суть метода эквивалентного генератора
состоит в нахождении тока в одной
выделенной ветви, при этом остальная
часть сложной электрической цепи
заменяется эквивалентным ЭДС Еэг,
с её внутренним сопротивлением
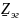 .
При этом часть цепи, в которую
входит источник
ЭДС называют
эквивалентным генератором или активным
двухполюсником, откуда и название
метода.
.
При этом часть цепи, в которую
входит источник
ЭДС называют
эквивалентным генератором или активным
двухполюсником, откуда и название
метода.
Для того чтобы найти эквивалентную ЭДС, нужно рассмотреть режим холостого хода генератора, другими словами нужно отсоединить исследуемую ветвь 23, тем самым избавив генератор от нагрузки, после чего он будет работать на так называемом холостом ходу (рис 2.4)
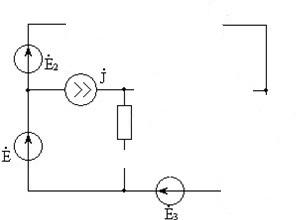
Рисунок 2.4
Напряжение холостого хода U23xх, будет равно эквивалентной ЭДС Eэг. Таким образом мы можем найти Eэг.
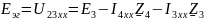
Найдем неизвестные токи, основываясь на метод контурных токов. Выберем 1 контурный ток, который будет проходить через источник тока. А для оставшихся составим уравнения (К=5-4+1-1=1 кол-во уравнений). Составим контурное уравнение для внешнего контура:
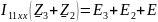
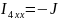
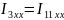
Решение:
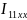 (
(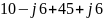 )
= 7.5
)
= 7.5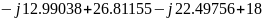
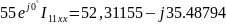
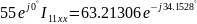
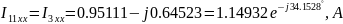 ,
тогда
,
тогда
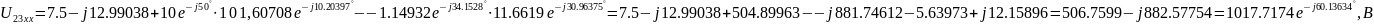
 рассчитывается
по формуле
рассчитывается
по формуле
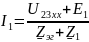 , ток
, ток
 и
и
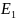 текут в одном направлении (рис 3.1) в
следствие этого +
текут в одном направлении (рис 3.1) в
следствие этого +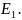
Следующим
этапом решения задачи будет нахождение
эквивалентного сопротивления
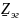 Можно
воспользоваться режимом короткого
замыкания генератора, при котором
сопротивление
Можно
воспользоваться режимом короткого
замыкания генератора, при котором
сопротивление
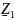 отсутствует
(рис 2.5).
отсутствует
(рис 2.5).

Рисунок 2.5
Найдем неизвестный ток, использую метод контурных токов. Выберем 1 контурный ток, который будет проходить через источник тока. А для оставшихся составим уравнения (К=6-4+1-1=2 кол-во уравнений):
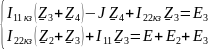
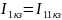
Решение:


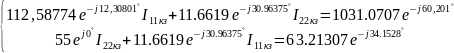
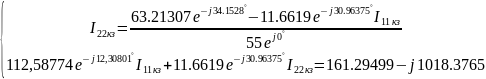
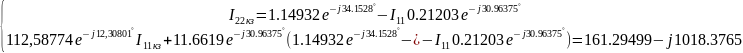
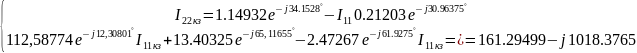

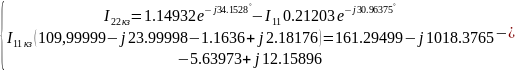
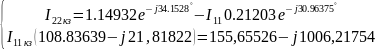

Отсюда
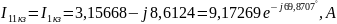 ,
,
следовательно,
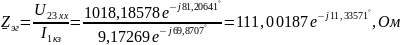
Тогда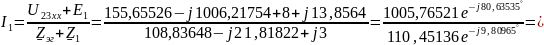
=
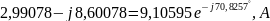
4) Проверить баланс комплексных мощностей в цепи.
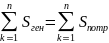
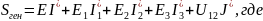
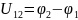 =
=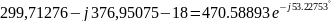 ,
B
,
B
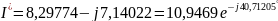 ,
A
,
A
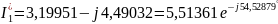 ,
A
,
A
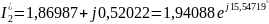 ,
A
,
A
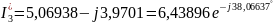 ,
A
,
A
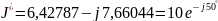 ,
A
,
A
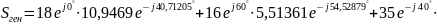
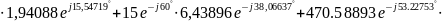
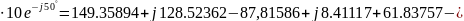
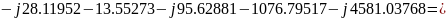

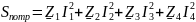

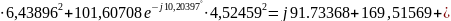
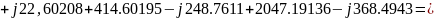
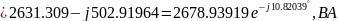
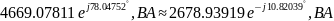
В результате расчетно-графической работы были выполнены поставленные цели: умение составлять систему уравнений по законам Кирхгофа для разветвленных электрических цепей однофазного синусоидального тока; рассчитывать токи методом контурных токов, методом узловых потенциалов в комплексной форме, методом эквивалентного генератора. Были сравнены результаты токов, полученные при методах контурного тока и узловых потенциалов и сведены в одну таблицу; просчитан комплексный ток и построен его график; проверен баланс комплексных мощностей.
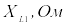
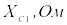
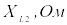
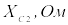
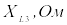
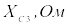
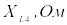
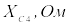
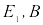
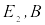
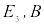
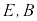
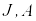
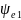 ,
град
,
град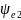 ,
град
,
град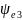 ,
град
,
град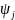 ,
град
,
град ,
град
,
град