Тема 2: Отношения, отображения, функции

Лекции 2 - 3

Цель: рассмотреть понятия соответствия, отношения, отображения, функции, их отличия, свойства; проиллюстрировать основные понятия на примерах.

План:

1. Понятие кортежа

2 Декартово произведение множеств

3. Бинарные отношения во множествах

4. Способы задания отношений

5. Свойства отношений

6. Отношение эквивалентности

7. Отношение порядка

8. Отображения множеств.

9. Функции

Литература: 1. Москвинова Г. И. Дискретная математика. Математика для менеджера в примерах и упражнениях : учебное пособие / Г.И. Москвинова – М. : Логос, 2000. – 240 с.: ил.

1. Понятие кортежа

Пусть даны множества А₁, А₃, …A_n. Выберем из первого множества элемент a₁, из второго – а₂ и т.д. Из множества А_n выберем элемент а_n. Расположим элемен­ты в порядке их извлечения. Получим упорядоченную последовательность (a_1, а₂,.... a_n).

Опр: Упорядоченная последователь­ность (а₁, а₂...a_n) составленная из элементов множеств A₁,A₂…A_n, где a_iA_i , i=1,2…n, - называется кортежем длины n. Заметим, что множества A₁, A₂,… А_n могут иметь общие элемента или даже совпадать. Поэтому элементы в кортеже могут повторяться.

О пр: Два кортежа, составленные из элементов одного и того же множе­ства А считаются равными, если их длины равны и элементы сто­ящие на соответствующих мес­тах, равны т.е.

m=n,

(a₁,a₂,…a_m)=(b₁,b₂,…b_n) a_k=b_{k ,}

1 kn,

где a_iA, b_jA,

i=1,2,…m, j=1,2,…n.

Таким образом, когда мы говорим:

а) о кортеже, то

1) учитываем порядок расположения элементов;

2) элементы в кортеже могут повто­ряться.

б) о множестве, то

1)не учитываем порядок расположения элементов;

2)ни один элемент множества не должен повторятся.

Опр: Элементы a₁,a₂,…a_n кортеже (a₁,a₂,…a_n) называются его компонентами или координатами.

2 Декартово произведение множеств

Опр: Декартовым произведением множествa A₁,A₂,…A_n называется множество, эле­ментами которого являются все кортежи длины n, составленные из элементов этих множеств.

Декартово произведение обоз­начают

A₁A₂…A_n  (a₁,a₂,…a_n)a_kA_k,1kn

Пример

1) А=б,и,г;

В={а,д;

АВ=(б,а);(б,д);(и,а);(и,д);(г,а);(г,д).

Пример

А={1,2};

В=3,4,5;

АВ=(1,3);(1,4);(1,5);(2,3);(2,4);(2,5)};

ВА={(3,1);(4,1);(5,1);(3,2);(4,2);(5,2)};

АВ  ВА.

Декартово произведение множеств не коммутативно.

Пример

(АВ)СА(ВС).

Так как ((a,b),c)(a,(b,c)),

то декартово произведение множеств не ассоциативно.

Пример

Пусть А=В=R, где R - множество действительных чисел,

тогда AB=RR=R²=(a,b)a,bR, ( рисунок 10).Каждую пару (а,b) можно изобразить точкой М(а,b) на координатной плоско­сти (рисунок 10). Связь с декартовой системой коорди­нат и объясняет название "декартово произведение множеств".

Рисунок –Декартово произведение множеств

Очевидно, что плоскость можно рас­сматривать как декартово произведение двух прямых линий (оси абсцисс и оси ординат) - каждая точка плоскости задаётся парой точек этих прямых.

---

Декартово произведение n элементов множества R называют n-мерным ариф­метическим пространством и обозначают Rⁿ= R R…R.

Пример

Пусть А и В - множества точек отрезков прямых (осей координат),

тогда АВ можно изобразить в виде множества точек прямоугольника (рисунок 11).

Рисунок –Декартово произведение множеств А и В

Пусть множества А и В конечны, при­чём А состоит из m элементов, а

В - из n элементов:

A={a₁,a₂,…a_m}; B={b₁,b₂,…b_n},

тогда АВ состоит из mn пар. Чтобы убедиться в этом, достаточно записать все пары, входящие в АВ в виде:

(a₁,b₁)…(a₁,b_n)

(a₂,b₁)…(a₂,b_n)

………………

(a_m,b₁)…(a_m,b_n)

Доказанное утверждение можно представить в виде равенства:

AB=AB,

где - число элементов множества А;

- число элементов множества В;

- число элементов декартова произведе­ния АВ.

3. Бинарные отношения во множествах

Опр.: Бинарное отношение ρ есть любое непустое подмножество декар­тового произведения двух множеств: ρ.

Бинарное отношение обозначается так: <х, у> ρ или х у или. Эти выражения эквивалентны и читаются как «х находится в отношении ρ к у».

Если рассматривается декартово произведение трех множеств, то говорят о тернарном отношении.

Пример

1. Отношениями могут служить:

х=у; ху; х > у; х < у в множестве Х действительных чисел;

2. х // у, х  у в множестве прямых плоскости;

3. Пусть X = {1,2, 3}, К = {1,2} рассматриваются как три издательства и два магазина, продающие книги. Тогда отно­шение ρ = {< 1,1 >, < 2, 2 >, < 3, 2 >} означает, что издательство I заключило договор с магазином 1, издательство 2-е магазином 2, издательство 3-c этим же магазином 2.

4. «х и у – родители z» - тернарное отношение.

5. Примером п -арного отношения, где п = 4, может служить таблица:

	Фамилия	Год рожд.	Место жительства	Образование
1	Иванов	1958	Оренбург	Высшее
2	…	…	…	…

Опр.: Областью определения бинарного отношения ρ (обозначение: D_ρ) называют множество первых координат элементов из ρ, областью значений отношения R (обозначение: E_ρ) — множество вторых координат элементов из ρ.

Например, областью определения для отношения мате­ринства служит множество всех матерей, в то время, как область значении этого отношения — множество всех людей.

4. Способы задания отношений

1. С помощью графика

Аналитическая геометрия плоскости основывается на допуще­нии о том, что между точками евклидовой плоскости и декартовым произведением R х R существует взаимно однозначное соответствие. Каждой точке на плоскости соответствуют ее координаты — упорядоченная пара <х, у>. Поэтому отношение на множестве R можно изображать па плоскости некоторой конфигурацией пли множеством точек. Например, отношение равенства можно изобра­зить в виде прямой у = х в декартовой системе координат.

---

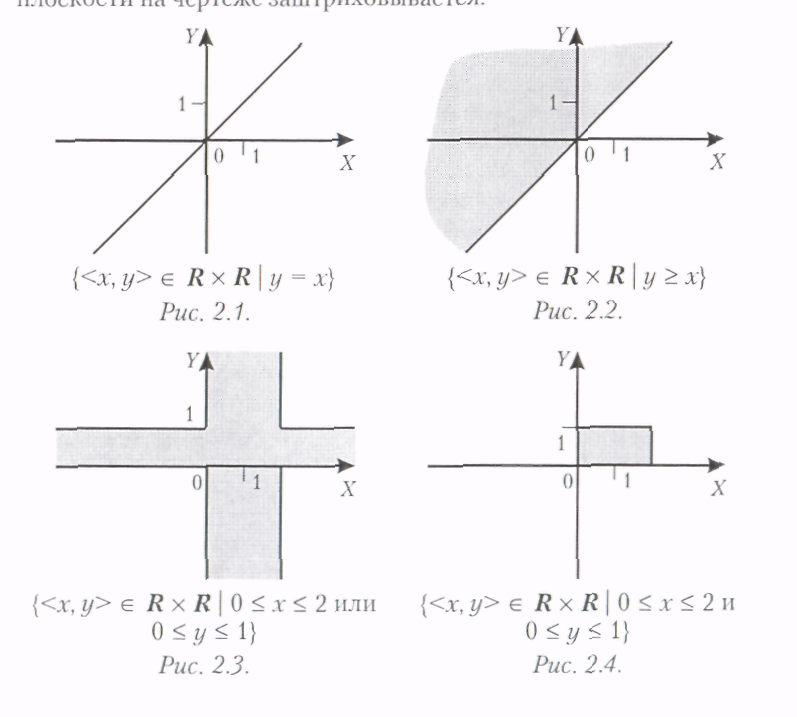
Опр. Если основным предметом изучения служат отношения на множестве действительных чисел R, то множество точек, соответствующих элементам отношения, называют графиком этого отношения.

Ниже на рис. приводятся четыре примера отношений, для каждого из которых схематически представлен его график. В тех случаях, когда график является частью плоскости, эта часть плоскости на чертеже заштриховывается.

2. C помощью графа

Е сли задано отношение х ρ у, хХ, уУ, то элементы множеств X и У можно изображать точками на плоскости, а упорядоченную пару — линией со стрелкой (дугой), направленной от х к у. Тогда отношение на конечном множестве элементов может быть представлено в виде графа.

Пример

Рассмотрим отношение "х делится на у" для множеств Х={20, 25, 30, 35, 40} и Y= {2, 3, 4, 5). Граф этого отношения имеет следующий вид:

3. Матричный способ задания отношении

Зададим отношение ρ: «х дружит с у» на множестве М, где М= {а₁, а₂, а₃, а₄} множество персонажей. Это отношение можно представить в виде таблицы (матрицы), элементы которой равны единице, если между соответствующими элементами есть отношение дружбы, и нулю в противном случае.

	а1	а2	а3	а4
а1	1	0	1	0
а2	0	1	0	0
а3	1	0	1	1
а4	0	0	1	1

Из этой таблицы видно, что а₁ дружит с а₃, а₂ не дружит ни с кем, кроме как с самим собой, а а₃ дружит со всеми, кроме а₂. Такой способ задания отношений называется матричным способом.

В этом случае отношение ρ ХхУ представляется в виде матрицы А = || а_ij || с элементами а_ij, где i - номер строки, j - номер столбца; а_ij = 1, если элементы х_i и y_j находятся в отношении ρ, и а_ij = 0 в противном случае.

Если || а_ij || = 0, то ρ≡ 0 - пустое отношение;

если || а_ij || = 1, то ρ≡ 1 - полное отношение.

5. Основные свойства отношений

Будем рассматривать отношения, заданные на множестве X, т.е. хρу, х, уX.

Опр. Отношение ρ на множестве X называется рефлексивным, если для любых х X выполняется хρх. Если для всех х  X не выполняется хρх, то отношение называется антирефлексивным.

Примеры. Отношение равенства рефлексивно. Отношение ху, х, у  R рефлексивно, так как хх. Отношение х > у, х, уR антирефлексивно, так как ни для одного числа не выполнимо х > х.

Опр. Отношение ρ на множестве X называется сим­метричным, если для любых хX, уX, из хρу следует уρх.

Иными слонами, отношение симметрично, если всякий раз, как выполняется хρу, выполняется и уρх.

Примеры. Из того, что «х родственник у», следует, что «у родственник х», - отношение симметрично. Отношение «х – сестра у», определенное на множестве всех людей, несимметрично: возможно, что у является братом х. Однако то же отношение, определенное на множестве женщин, является симметричным.

Опр. Отношение ρ на множестве X называется антисимметричным, если для любых х, у  X, из того, что хρу и уρх, следует х = у.

---

Примеры. Отношение х у антисимметрично: из того, что х у и ух, следует, что х = у, т.е. это один и тот же элемент.

Опр. Если для любых х, у  Х из того, что хρу, следует, что не выполняется уρх, то отношение называется асимметричным.

Отношения «х предок у» и «у потомок х» асимметричны, причем второе является обратным к первому. Отношение строгого порядка х < у является асимметричным: если выполняется х < у. то не выполняется у < х.

Опр. Отношение ρ называется транзитивным, если из того, что хρу и yρz, следует xρz.

Пример. Отношение «х предок у» транзитивно: если «х предок у» и «у предок z», то «х предок z». Отношение х < у, где х, у  R,транзитивно: если х < у и у < z, то х < г. Отношение «х любит у», в общем случае нетранзитивно: если «х любит у», а «у любит z», то из этого не следует, что «х любит z».

6. Отношение эквивалентности

Опр. Отношение, которое обладает свойствами рефлексивности, симметричности и транзитивности, называется отношением эквивалентности.

Примеры отношений эквивалентности.

1. Отношение параллельности прямых в евклидовом пространстве есть отношение эквивалентности.

2. Утверждения вида sin²x + cos²x = 1, (а + b)(a - b) = а² - b², состоящие их формул, соединенных знаком равенства, задают би­нарное отношение на множестве формул, описывающих суперпози­ции элементарных функций. Это отношение равносильности также является отношением эквивалентности: формулы равносильны, если они задают одну и ту же функцию.

3. Отношение «студенты х и у учатся в одной группе», где х, у {«студенты первого курса»}, есть отношение эквивалентности.

4. Отношение «жить в одном районе», определенное па множестве людей, живущих в г. Оренбург, является отношением эквивалентности. Множество всех жителей Оренбурга разбивается последним отноше­нием эквивалентности на ряд непересекающихся подмножеств, в данном случае на множества людей, живущих в одном и том же районе. Два жителя считаются эквивалентными по данному отноше­нию, если они живут в одном и том же районе, и в этом смысле они неразличимы, т.е. они обладают одним и тем же свойством: «жить в районе «XXX». Это свойство является определяющим свойством множества всех жителей района «XXX». С другой стороны, нельзя жить в двух (и более) районах сразу (во всяком случае, согласно прописке), поэтому множества жителей различных районов не пересекаются. Таким образом, отношение «жить в одном районе» разбивает все множество жителей города на ряд непересекающихся подмножеств, таких, что внутри каждого подмножества все жители эквивалентны по данному отношению, и никакие два жителя разных подмножеств не находятся в отноше­нии эквивалентности друг с другом. Такие подмножества называ­ются классами эквивалентности. Ладим более строгое определение.

Опр. Пусть на множестве X задано отношение эквивалентности ρ. Тогда подмножество А X называется классом эквивалентности по отношению ρ, если А состоит из всех тех элементов х  X, что для некоторого а  X, а  А и хρа.

---

Можно построить классы эквивалентности следующим образом. Выберем элемент а₁, принадлежащий X, и образуем подмножество A₁X из а₁ и всех элементов, эквивалентных а₁. Это будет класс эквивалентности A₁. Далее выберем элементу а₂ Х, а₂ ≠ А₁ и образу­ем класс А₂, состоящий из всех элементов, эквивалентных а₂ и т. д.

Получим систему классов А₁, А₂, … такую, что любой элемент а_i  X входит только в один класс, объединение всех классов А₁ А₂ ... образует множество X, и для любых i, j Аi ∩ Аj = , т.е. множество классов эквивалентности образует разбиение множества X.

Опр. Отношение на множестве X называется эквивалентностью, если существует разбиение X на подмножества {A₁, A₂ ,...,A_n} такое, что отношение хρу выполняется тогда и только тогда, если х и у принадлежат одному и тому же подмножеству.

Будем обозначать класс эквивалентности, порожденный элемен­том а X через [a]. Тогда, если aρb, то [а]=[b].

Опр. Множество классов эквивалентности множе­ства X по отношению ρ называется фактор-множеством множе­ства X по отношению ρ и обозначается [X/ρ].

Примеры.

1. Свойство параллельности прямых на плоскости определяет
   отношение эквивалентности.

2. Типичным примером отношения эквивалентности является отношение равенства (=) на множестве чисел. Очевидно, что лю­бое число а из множества действительных чисел равно самому се­бе. Если а = b, то b = а. Если а =b, а b = с, то а = с.

7. Отношение порядка

Отношения х <у, х> у в множестве дей­ствительных чисел, "человек х меньше че­ловека у" в множестве людей, "яблоко х тяжелее яблока у" в множестве яблок и многие другие отношения обладают общи­ми свойствами, а именно: они транзитивны, асимметричны. Асимметричные и транзитивные отношения встречаются во многих случаях. Поэтому их выделяют в особый класс отношений, называемых от­ношениями строгого порядка.

Опр. Отношение R на множестве X называется отношением нестрого порядка, если оно рефлексивно, антисим­метрично и транзитивно.

Отношения на множестве чисел X являются отношениями нестрогого порядка, так как любое число х  X равно самому себе (рефлексивность).

Для любой пары чисел x, у  X при а b не выполняется ba, а при а b не выполняется bа (антисимметричность). Для лю­бой тройки чисел х, у, z  X, если а b и b с, то а с или, если а b, bс, то а с (транзитивность).

Опр. Отношение R на множестве X называется отношением строго порядка, если оно антирефлексивно, анти­симметрично и транзитивно.

Отношения <, > на множестве чисел X являются отношения­ми строгого порядка, так как любое число х  X не может быть меньше или больше самого себя (антирефлексивность). Для лю­бой пары чисел х, у  X при х < у не может быть у < х, а при х > у не выполняется у > х (антисимметричность). Для любой тройки чисел х, у, z  X, если х < у, а у < z, то х < z и, если х>у, a у> z, то х > z (транзитивность).

Опр. Множество Х с заданным на нем отноше­нием нестрогого или строгого порядка R называется упорядочен­ным и обозначается парой < X, ρ >.

---

Смотрите также файлы

• ПРим, Краскал.docx

• лекция 4-6.doc

• Множества.docx

• конспект.doc

• Вопросы.doc