1.4.1. ПРЯМЫЕ ИОБРАТНЫЕ ЗАДАЧИ ГРАВИРАЗВЕДКИОсновой теории интерпретации данных гравиразведки является решение прямых и обратных задач. Прямая задача гравиразведки состоит в определении элементов поля силы тяжести по заданному распределению его источников, когда известны форма, размеры, глубина залегания и величина эффективной плотности. Обратная задача гравиразведки ставит противоположную цель: нахождение параметров объекта (формы, размеров, глубины залегания, эффективной плотности) по известному распределению (на профиле или на площади) элементов силы тяжести.Решение прямой задачи в общем виде. Аномалии силы тяжести, вызванные притяжением тел известной формы, размера и избыточной плотности, рассчитывают на основе закона всемирного тяготения (закона Ньютона).Для этого притягивающее тело разбивают на элементарные массы (dm); рассчитывают аномалию такой точечной массы (Δg₁), которая равна вертикальной составляющей силы (F₁) ньютоновского притяжения этой массой массы, равной 1 г, находящейся в точке наблюдения А, т. е. берут составляющую силы притяжения по направлению действия силы тяжести Земли (g); наконец, используя принцип суперпозиции, определяют аномалию за счет притяжения всем телом (Δg_T) как сумму притяжений всех элементарных точечных масс, которыми можно представить аномалообразующее тело (рис. 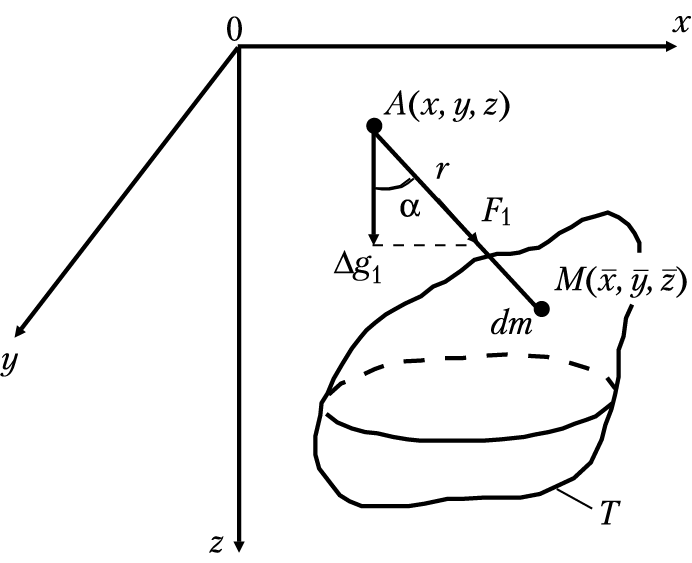1.5).Рис. 1.5. Схема определения аномалий силы тяжестиот элементарной массы (dm) и гравитирующего тела (Т)Математически это может быть выражено следующим образом. 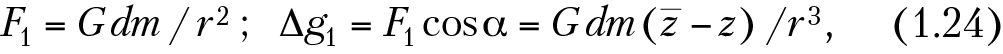Согласно выражению (1.1):где —расстояние между точкой наблюдения А (х, у, z) и точкой , в которой находится элементарная точечная масса (dm). В природных условиях аномальные включения с плотностью σ находятся во вмещающей среде с плотностью σ₀, поэтому под массой dm надо понимать избыточную массу: dm = (σ — σ₀)dV = ΔσdV, где dV — элементарный объем точечной массы; Δσ — эффективная плотность.

---

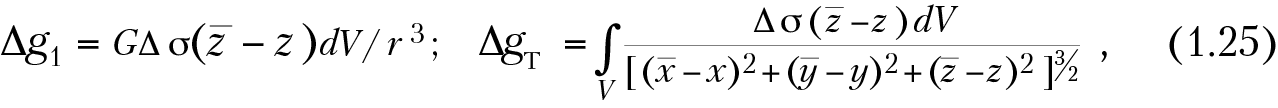
Окончательные выражения для расчета аномалии силы тяжести точечной массы и тела, используемые в теории гравиразведки, имеют видИнтеграл в последней формуле берут по всему объему тела (V). При σ > σ₀ значения Δg_T имеют положительный знак, т. е. наблюдаются увеличение притяжения и положительные аномалии. При σ < σ₀ значения Δg_T имеют отрицательный знак, т. е. наблюдаются уменьшение притяжения и отрицательные аномалии.Аналитические решения с помощью уравнения (1.25) получаются лишь для тел простой геометрической формы (шар, цилиндр и др.) с постоянным значением эффективной плотности. Для тел более сложной формы, особенно с переменной плотностью, возможны лишь численные решения интеграла (1.25) на основе сложных вычислительных схем. Анализ решений прямых задач служит основой при разработке приемов решения обратных задач гравиразведки для типовых геологических структур и объектов аналитическим методом.Рассмотрим несколько примеров решения прямых и обратных задач для тел правильной геометрической формы.Прямая и обратная задачи для шара. Пусть однородный шар радиусом R, объемом V, с избыточной плотностью Δσ расположен на оси Z на глубине h (рис. 1.6). Решим прямую задачу, т. е. определим гравитационный эффект вдоль наземного профиля ОХ, проходящего через проекцию центра шара с началом координат над ним. 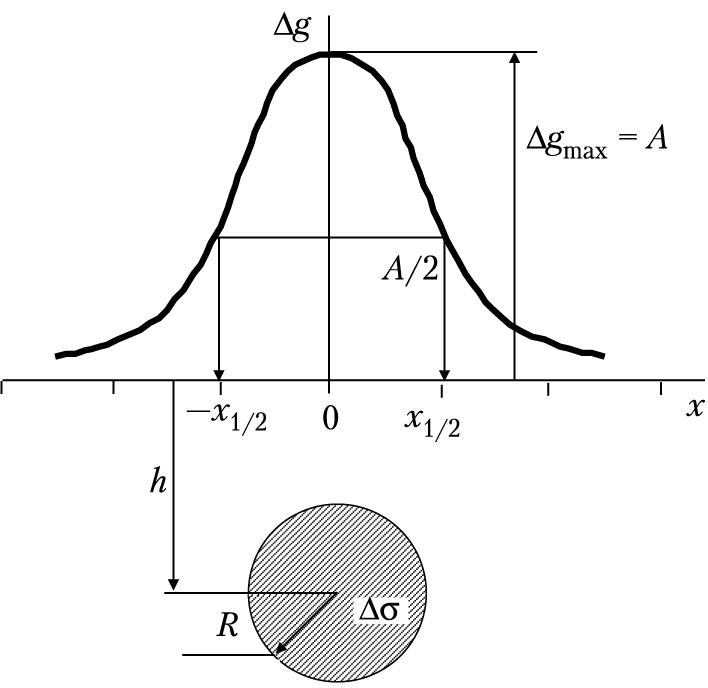Поскольку по закону всемирного тяготения шар притягивается с такой же силой, что и точечная масса, сосредоточенная в его центре, аномалию над шаром (Δg_ш) можно получить без решения интеграла (1.25), считая, что аномалия силы тяжести над шаром и аномалия точечной массы, помещенной в его центре, совпадают:Рис. 1.6. 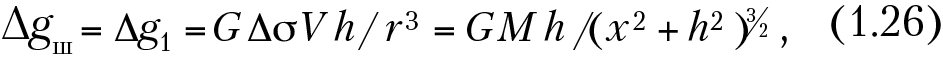Гравитационная аномалия (∆g(х)) от модели в виде шараили горизонтального стержня (цилиндра) при Δσ > 0где M = ΔσV — эффективная масса шара.График Δg_ш будет иметь максимум (при Δσ >0) над центром шара Δg_max(0) = GM/h² = А и асимптотически стремиться к нулю при х → ± ∞ (см. рис. 1.6). Знак Δ

---

g_ш определяется знаком Δσ. Если провести расчеты по ряду профилей, то очевидно, что карта изолиний Δg_ш будет иметь вид концентрических окружностей с центром над шаром, т. е. аномалия Δg_ш в плане на плоскости х0у будет изометричной.Из анализа уравнения (1.26) и графиков на рис. 1.6 можно решить обратную задачу. Например, найдем абсциссу x_1/2, в которой Δg_ш достигает половины максимума:откуда (x²_1/2 + h²)^3/2 = 2h³. Решив это уравнение, получим:|x_1/2| = 0,76 h или h = 1,31 |x_1/2|. (1.28)Таким образом, определив по графику Δg_ш значения Δg_max, 1/2 ⋅ Δg_max и абсциссу точки кривой x_1/2, где Δg_ш = 1/2 ⋅ Δg_max, и умножив ее на коэффициент 1,31, можно найти глубину залегания центра шарообразного объекта (h). Далее можно рассчитать эффективную массу (M = Δg_maxh²/G), а зная Δσ, определить радиус (R) или, зная R, получить значение ∆σ (табл. 1.2).Таблица 1.2. Основные результаты решения прямой и обратной задач гравимагниторазведки

№ п/п	Модель объема	Формула расчета аномалии		Форма аномалии вдоль профиля 0Х		Характер аномалии на плоскости Х0Y		Амплитуда (σ0) аномалии (A)		Соотношение параметров аномалии и характеристик тела
		∆gа(х)	∆Zа(х)	∆gа(х)	∆Zа(х)	∆gа(х, у)	∆Zа(х, у)	∆gа(х)	∆Zа(х)	∆gа(х)	∆Zа(х)
1	Шар			один знак, один экстремум	два знака, три экстремума	изометричный	изометричный				IV =Ah3
2	Вертикальный стержень (цилиндр)	—		один знак, один экстремум	один знак, один экстремум	изометричный	изометричный	—		—	IS=Ah2
3	Горизонтальный стержень (цилиндр)			один знак, один экстремум	два знака, три экстремума	линейный	линейный				IS = Ah/2
4	Вертикальный пласт	—		один знак, один экстремум	один знак, один экстремум	линейный	линейный	—		—	I2bS = Ah/2

---

Примечание:  — абсцисса точки аномальной кривой, в которой значение функции равно нулю; — абсцисса точки аномальной кривой, в которой значение функции составляет половину амплитуды аномалии.В геологической практике модель шара часто используется при аппроксимации интрузий батолитового типа, многих полиметаллических месторождений, карстовых образований и др.Прямая и обратная задачи для горизонтального кругового цилиндра. Пусть горизонтальный бесконечно длинный круговой цилиндр радиуса R, сечения S, с избыточной плотностью ∆σ расположен вдоль оси у на глубине h (см. рис. 1.6).Решим прямую задачу, т. е. определим Δg_ГЦ вдоль оси х, направленной вкрест простирания цилиндра с началом координат над его центром. Притяжение цилиндра будет таким же, как притяжение вещественной линии, расположенной вдоль его оси с массой единицы длины dm = SΔσdy. 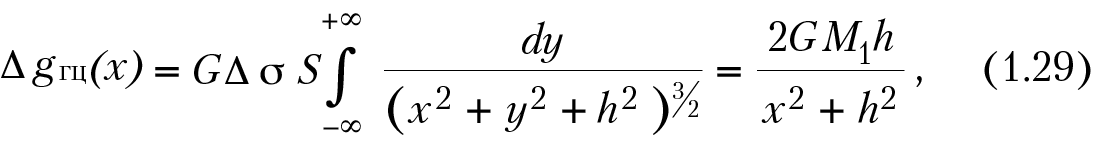Поэтому для точек наблюдения вдоль оси х (y = z = 0) с учетом того, что х = 0, –∞ < y < +∞ (цилиндр считается бесконечно длинным) и z = h, аналитическое выражение можно получить из уравнения (1.25):где М₁ = SΔσ — эффективная масса единицы длины цилиндра.График Δg_ГЦ будет иметь максимум (при Δσ > 0) над центром структуры Δg_max(0) =  2GM₁/h = А и, как и Δg_ш, асимптотически стремиться к нулю при х → ± ∞. В целом график Δg_ГЦ вдоль оси х будет примерно таким же, как и над шаром. Очевидно, что в плане изолинии Δg_ГЦ будут представлять систему параллельных оси цилиндра линий, т. е. 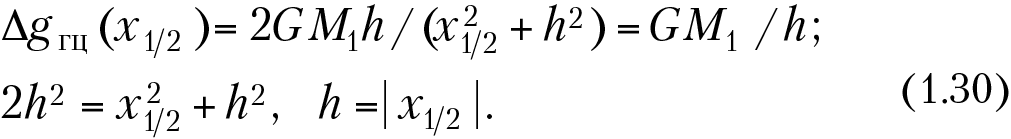аномалия Δg_ГЦ в плоскости х0у будет линейной.Решим обратную задачу для горизонтального бесконечно длинного кругового цилиндра тем же приемом, что и для шара:Таким образом, определив по графику Δg_ГЦ значение Δg_max, ¹/₂ Δg_max и абсциссу x_1/2, можно получить глубину залегания оси цилиндра (h) и далее рассчитать единичную эффективную массу (M₁ = ∆σS = Δg_maxh/2G), а зная Δσ, можно определить площадь поперечного сечения цилиндра (S = πR² = M₁/Δσ) или его радиус (R

---

), или, зная R, рассчитать ∆σ (см. табл. 1.2).

В реальных условиях модель горизонтального цилиндра применяется при аппроксимации валообразных поднятий фундамента, протяженных складчатых структур осадочного чехла, техногенных образований и пр.

Прямая и обратная задачи для вертикального уступа. Под вертикальным уступом в теории интерпретации гравитационных аномалий понимают горизонтальный полупласт, ограниченный вертикальной гранью, бесконечно простирающийся по оси y в какую-либо сторону от начала координат (рис. 1.7). Плотность пород уступа и вмещающих пород различна и составляет постоянную и отличную от нуля величину Δσ. Если глубину верхней горизонтальной плоскости, ограничивающей полупласт, обозначить h₁, нижней — h₂, а боковую вертикальную грань совместить с осью Z, то гравитационное поле Δg_уст в точках x (вдоль оси х при z = 0 и y = 0) соответствует выражению (1.25) при определенных пределах интегрирования и может быть выражено аналитически:



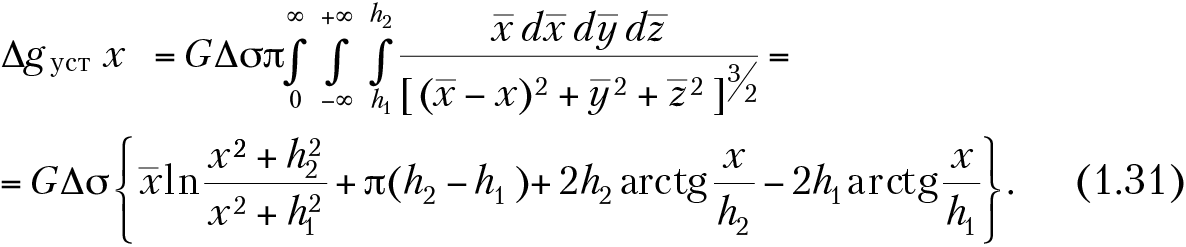
Вид кривой Δg_уст (при σ > σ₀) приведен на рис. 1.7. При х → ±∞ значения Δg выходят на горизонтальные асимптоты с максимальной амплитудой Δg_max = 2πGΔσΔh. Над самим вертикальным сбросом (при х = 0) получаем Δg = 1/2 ⋅ Δg_max = πGΔσΔh. Очевидно, на карте Δg_уст будут наблюдаться параллельные изолинии с максимальным сгущением изолиний над вертикальной гранью. Из выражения (1.31) можно получить для абсцисс точек с x_1/4 и x_3/4, в которых Δg_уст составляет ¹/₄ и ³/₄ от Δg_max, выражение для определения средней глубины залегания вертикального уступа:

h_ср = (h₁ + h₂)/2 = x_1/4 = x_3/4. (1.32)

Если известна избыточная плотность (Δσ), то можно определить мощность вертикального уступа ∆h = Δg_max/2πGΔσ и рассчитать глубину залегания верхней (h₁ = h_cp – Δh/2) и нижней (h₂ = h_cp + Δh/2) кромок. Зная ∆h, можно рассчитать величину ∆σ.



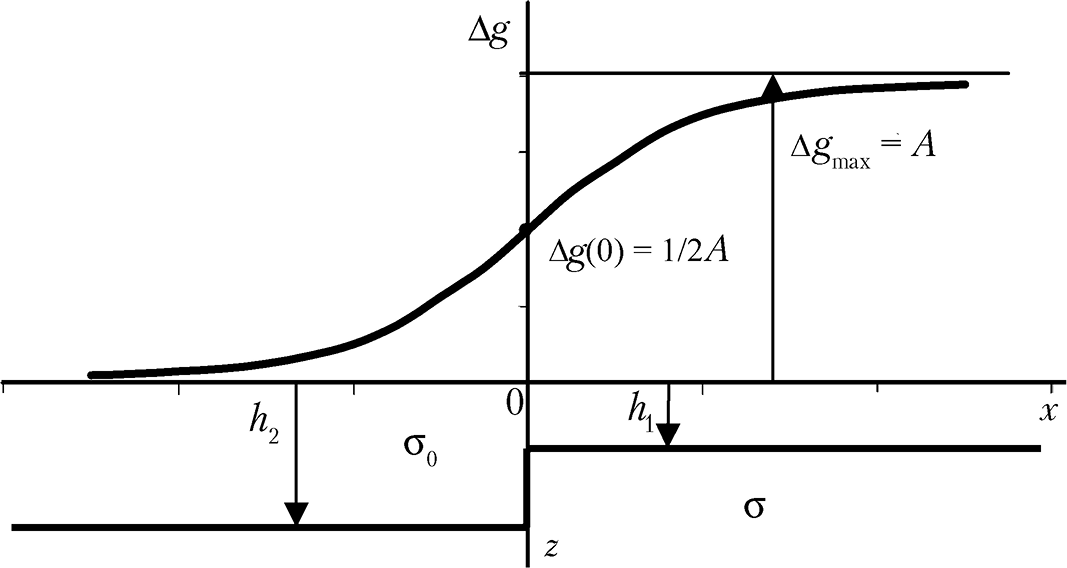
Рис. 1.7. Аномалия силы тяжести «гравитационная ступень»
от модели плотностной неоднородности в виде вертикального уступа

Моделью вертикального уступа часто

---

Смотрите также файлы

• .docx

• Эмоциональноволевые процессы и состояния.docx

• А метиловый оранжевый.docx

• Курсовая работа.docx

• Сегодня 15 23 Сила тока. Единицы силы тока. Амперметр.pptx