9 вариант

Задание 6

1. Пусть M(x) означает «х есть птица» , L(x) означает «х умеет летать» Что означают утверждения: M(орел)

 L(страус)

x M(x)


Какие из них истинны, какие нет?

Решение:

В условии задано: предикат M(x) означает «х есть птица».

Это означает, что предикат M(x), задающий принадлежность к классу птиц, имеет интерпретацию. Тогда формуле может быть приписано значение «истина» или «ложь».

M(орел)

В предикате M(x) переменная x заменена на конкретную величину (константу) : «Орел является птицей». Выражение принимает значение И.

В условии задано: предикат L(x) означает «х умеет летать».

Это означает, что предикат L(x), задающий принадлежность к умеющим летать, имеет интерпретацию. Тогда формуле может быть приписано значение «истина» или «ложь».

 L(страус)

В предикате L(x) переменная x заменена на конкретную величину (константу) : «Страус не является летающим». Выражение принимает значение И.

Рассмотрим формулу x M(x).

Предикат M(x) означает «х есть птица».

Формула не содержит ни одной константы, но переменная связана квантором:

«Найдется такой х, что х-птица». Такой формуле припишем значение Истина.

Как записать утверждения:

«Не все птицы летают» - ∀x L(M(x))

«Пингвин - птица» - M(пингвин)

«Канарейка – птица, умеющая летать» - L(M(канарейка))

дельфины

Задание 7

Все дельфины относятся к китообразным. Ни одна рыба не является китообразной. Следовательно, ни одна рыба не является дельфином. Введём предикаты, которые используются в рассуждении:

K(x) означает, что x — относится к китообразным,

D(x) — что x — является дельфином,

R(x) — что x — является рыбой.

Формализация рассуждения:

∀x (D(x) → K(x))

¬(∀x (R (x) → K (x)))

-----------------------------

¬(∀x (R (x) → D (x)))

Задание 10

Докажем рассуждение «от противного», построив логическое произведение посылок и отрицания заключения.

Посылка 1∀x (D(x) → K(x))= ∀x (¬D(x) ∨ K(x))формула преобразована к ПНФ.

Посылка 2: ¬(∀x (R (x) → K (x)))= ¬(∀x (¬R (x) ∨ K(x)))= ∃x (R (x) & ¬K(x)) формула преобразована к ПНФ.

Отрицание заключения: ∀x (R (x) → D (x)))= ∀x (¬R (x) ∨ D (x)) формула преобразована к ПНФ.

Преобразование Сколема и получение множества дизъюнктов.

---

Посылка 1: при отсутствии кванторов существования совпадает со Сколемовской стандартной формой. Получаем дизъюнкт:

¬D(x) ∨ K(x)

Посылка 2:

Применяем преобразование Сколема, вычёркивая квантор существования.

Получили два дизъюнкта: R (x), ¬K(x)

Отрицание заключения: при отсутствии кванторов существования совпадает со Сколемовской стандартной формой. Получаем дизъюнкт:

¬R (x) ∨ D (x)

Методом резолюции вывести пустой (тождественно ложный) дизъюнкт из исходного множества:

S = { ¬D(x) ∨ K(x), R (x), ¬K(x), ¬R (x) ∨ D (x)} содержащего четыре дизъюнкта, доказав тем самым справедливость рассуждения.

D1: ¬D(x) ∨ K(x)

D2: R (x)

D3: ¬K(x)

D4: ¬R (x) ∨ D (x)

--------------

D5: ¬D(x) (резольвента D1 и D3).

D6: ¬R (x) (резольвента D4 и D5).

D7: (резольвента D6 и D2).

Получен пустой дизъюнкт.

Задание 12

Класс1 <1 , 2> <2 , 3> <3 , 3>

Класс 2 <6 , 1 > < 7 , 2> <9 , 1>

Изобразим точки на плоскости:



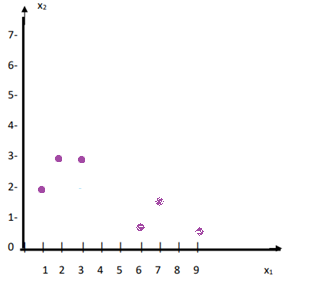
Выполняем итерацию 1. Выбираем первый объект класса С1 – вектор Х1=<1 , 2>. Значение функции FX1   0  01 0 2  0, (ошибка классификации произошла в первой же точке из шести, так как точка <1 , 2> принадлежит классу 1 и функция F(<1 , 2>) должна дать значение больше нуля, а не нулевое ). Таким образом, по правилу П8 алгоритма необходима коррекция коэффициентов при значении множителя с=1. Вычисляем новые коэффициенты функции:

Получаем F¹ X =1 x₁  2 x₂.

Выполняем итерацию 2. Вычислим последовательно значения F X  ¹ для элементов выборки:

F¹(<1 , 2>) =1+1+4=6>0 F¹(<2 , 3>) =1+2+6=9>0 F¹(<3 , 3>) =1+3+6=10>0

Все элементы класса С₁ распознаны правильно. Выбираем текущим класс С₂.

F¹(<6 , 1 >) =1+6+2=9>0 объект распознан неправильно. Необходима коррекция коэффициентов при значении множителя с=-1.

Новая функция F² X =x₂ -5x₁.

Выполняем итерацию 3. Вычисляем значения функции для элементов выборки

F²(<1 , 2>) =2-5=-3<0 объект распознан неправильно. Необходима коррекция коэффициентов при значении множителя с=1.

Новая функция F³ X =1-4x₁  3 x₂.

Выполняем итерацию 4. Вычислим последовательно значения F X  ³ для элементов выборки:

F³(<1 , 2>) =1-4+6=3>0 F³(<2 , 3>) =1-8+9=2>0 F³(<3 , 3>) =1-12+9=-2<0 объект распознан неправильно. Необходима коррекция коэффициентов при значении множителя с=-1.

---

Новая функция F⁴ X =-7x₁

Выполняем итерацию 5. Вычислим последовательно значения F X  ⁴ для элементов выборки:

F⁴(<1 , 2>) =-7<0 объект распознан неправильно. Необходима коррекция коэффициентов при значении множителя с=1.

Новая функция F⁵ X =1-6x₁  2 x₂.

F⁵(<1 , 2>) =1-6+4=-1<0 объект распознан неправильно. Необходима коррекция коэффициентов при значении множителя с=-1.

Новая функция F⁶ X =-7x₁, данная функция равна F⁴ X =-7x_1, невозможно получить линейную разделяющую функцию.0>1>0>1>0>3>2>1>0>1>6>3>2>1>1>1>1>9>6>3>2>1>

---

Смотрите также файлы

• Н. контр. Руководитель е. Г. Товбаз Е. Г. Товбаз студент группы 9 срб1 Бобоева Ш. А.docx

• Лекции д э. н., профессора Сидоренко Юрия Александровича.docx

• Государственнаяобразовательнаяорганизациявысшегопрофессиональногообразования донецкийнациональныймедицинскийуниверситетименим. Горького.docx

• Содержание раздел i общая характеристика предприятия, организации. Общие сведения об организации.docx

• Б. Х. Жангельдин жыл.docx