Файл: Статистика.docx

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТВЕРСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»

Кафедра бухгалтерского учета, финансов, АЭД и аудита

СТАТИСТИКА

Реализация статистического анализа в среде MS Excel

Методические указания для самостоятельной работы студентов

по дисциплине «Статистика»

для студентов экономического и технологического факультета

(направление 080100.62 - Экономика, профиль - Бухгалтерский учет, анализ и аудит, направление 080200.62 - Менеджмент, профиль - Производственный менеджмент направление 100800.62 - Товароведение профиль - Товароведение и экспертиза товаров (в сфере производства и обращения сельскохозяйственного сырья и

продовольственных товаров)

Тверь, 2014

Методические указания для самостоятельной работы студентов по дисциплине «Статистика» подготовленные к.э.н., доцентом кафедры «Бухгалтерский учет, финансы, АЭД и аудит» Егоровой Е.В. обсуждены и рекомендованы к изданию на заседании кафедры (протокол № от 20 г.)

Рецензент: доцент кафедры бухгалтерского учета, анализа и аудита ТвГТУ Мутовкина Н.Ю., к.т.н., доцент

Настоящие методические указания одобрены на заседании методической комиссии экономического факультета (протокол № от 20 г.)

СОДЕРЖАНИЕ

Введение

Основная задача и предназначение статистики состоит в том, чтобы помочь людям лучше понять многие проблемы, с которыми мир сталкивается в настоящее время.

Благодаря появлению большого количества пакетов программ, позволяющих решать задачи статистического анализа данных на компьютерах, методы статистического анализа находят все более широкое применение, как в различных областях науки, так и в практической деятельности.

В настоящее время насчитывается более тысячи пакетов, решающих задачи статистического анализа данных в среде операционной системы Windows. Число статистических пакетов, получивших распространение в России, достаточно велико и спрос на них продолжает возрастать. Однако одним из самых доступных и популярных средств компьютерного анализа данных остается MS Excel.

Самостоятельная работа направлена на формирование и развитие у студентов следующих компетенций:

• способность собрать и проанализировать исходные данные, необходимые для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов;

• способность выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы;

• способность анализировать и интерпретировать данные отечественной и зарубежной статистики о социально-экономических процессах и явлениях, выявлять тенденции изменения социально-экономических показателей;

• умение применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели.

Использование в процессе обучения программного продукта позволит избежать нудных расчетов, активирует творческое мышление обучающегося, сделает процесс статистического исследования увлекательным.

Задание к теме «Представление статистических данных:

таблицы и графики»

Используя данные Российского статистического ежегодника за 2013 год (http:// www. gks .ru/) или данные сайта Единой межведомственной информационно-статистической системы (http://www.fedstat.ru), постройте средствами MS Excel следующие виды графиков:

• одномерный график динамики с двумя переменными;

• столбиковую диаграмму структуры;

• ленточную диаграмму.

Исходные данные для построения графиков оформите в таблицы.

Под каждым графиком сделайте аналитические выводы.

Вариант 1. Графики численности, состава и структуры населения (по данным РФ, ЦФО или Тверской области).

Вариант 2. Графики движения населения: рождаемость, смертность, миграция (по данным РФ, ЦФО или Тверской области).

Вариант 3. Графики, характеризующие труд и занятость (по данным РФ, ЦФО или Тверской области).

Вариант 4. Графики, характеризующие доходы населения (по данным РФ, ЦФО или Тверской области).

Вариант 5. Графики состояния и развития сельского хозяйства (по данным РФ, ЦФО или Тверской области).

Вариант 6. Графики состояния и развития растениеводства (по данным РФ, ЦФО или Тверской области).

Вариант 7. Графики состояния и развития животноводства (по данным РФ, ЦФО или Тверской области).

Вариант 8. Графики состояния и развития розничной торговли (по данным РФ, ЦФО или Тверской области).

Вариант 9. Графики состояния и развития денежно-кредитной системы (по данным РФ, ЦФО или Тверской области).

Вариант 10. Графики динамики, состава и структуры инвестиций (по данным РФ, ЦФО или Тверской области).

Методические указания по выполнению работы

Таблицы в MS Excel создаются на рабочем листе, который разделен на строки и столбцы (графы). В образованные в результате пересечения строк и столбцов ячейки вводится содержимое таблицы. Размер таблицы определяется произведением числа строк на число граф.

При составлении таблицы в MS Excel рекомендуется сначала записать заголовки, учитывая размерность таблицы, затем отформатировать ее должным образом и только потом заполнить данными. На рис.1 представлен первый этап формирования таблицы.

А2 2

■ В ill; 1 a ,fo

г. Москва

Таблица 1 - Численность экономичеки активного населения в ЦФО, тыс. человек Регион Год

3. 2005 2006 2007 2008 2009 2010 2011 2012

4. Центральный федеральный округ

5. Белгородская область S Брянская область

7 Владимирская область s Воронежская область э Ивановская область 1С Калужская область Костромская область Курская область Липецкая область Московская область Орловская область Рязанская область Смоленская область Тамбовская область Тверская область Тульская область Ярославская область г. Москва |i

н| Лист! /Лист! [2) /Лист! (3) /Лист2 /<п. ^

Рис.1. Первый этап формирования статистической таблицы в MS Excel

На листе MS Excel в соответствующих ячейках записаны верхние и боковые заголовки таблицы. Поскольку никаких приемов форматирования на данном этапе не использовалось, то заголовки таблицы оказались записаны в одну строку и тем шрифтом, который указан в параметрах MS Excel по умолчанию.

На втором этапе составления таблицы применяются соответствующие методы форматирования ячеек (рис.2), в частности: изменение типа и размера шрифта, объединение ячеек, перенос слов в ячейках, выравнивание текста, изменение ширины столбцов и высоты строк, добавление и изменение границ таблицы. При желании можно также изменить цвет шрифта, границ, фона отдельных элементов либо таблицы в целом, начертание шрифта (полужирный, курсив, подчеркнутый и т.п.), расположение текста в ячейках таблицы и т.п.

Рис.2. Второй этап формирования статистической таблицы в MS Excel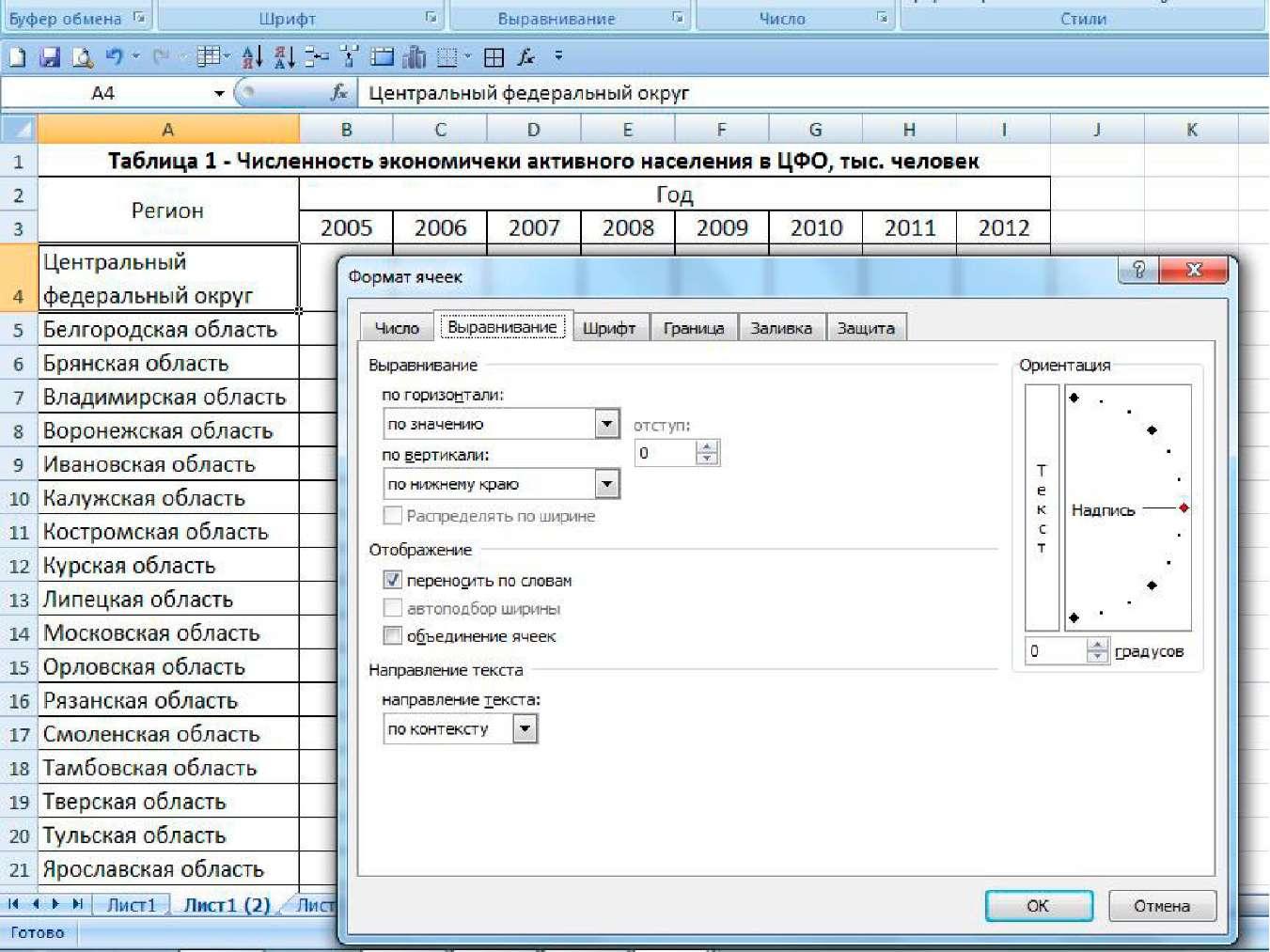

Третий этап формирования статистической таблицы в MS Excel заключается в заполнении ее данными (рис.3).

Л |

"77

Рис.3. Заключительный этап формирования статистической

таблицы в MS Excel

Ш

MS Excel предоставляет широкие возможности визуализации данных. Удобным средством для создания графических представлений в Excel является Мастер диаграмм, который вызывается на вкладке Вставка^ Диаграммы

(рис.4).

Рис.4. Мастер диаграмм - Выбор типа диаграммы

16 17

is

19 2C 21 22

26. 27 2S 29 3C

    33. 54

Также редактирование диаграммы возможно на вкладке Главного меню Макет.

Пример выполнения работы

Рис.6. Вызов контекстного меню форматирования диаграммы

Таблица 1 - Выпуск специалистов образовательными учреждениями Тверской области, реализующими программы высшего профессионального образования

Источник: http://www.fedstat.ru

Рис. 7. Динамика выпускников учреждений высшего профессионального

образования в Тверской области

Рис.8. Структура выпускников учреждений высшего профессионального образования в Тверской области по формам образовательных учреждений

Как видим из представленных данных, численность выпускников высших учебных заведений увеличилась с 6 285 человек в 2005 году до 7 899 человек в 2012 году. Пик численности выпускников пришелся на 2010 год. В этом году число выпускников вузов составило 8 391 человек.

На графике (рис.7) отчетливо видно, что численность выпускников государственных вузов росла более медленными темпами по сравнению с общей численностью выпускников. На рисунке 8 показано, что в структуре выпускников за рассматриваемый период доля выпускников негосударственных вузов увеличилась с 5,9% в 2005 году до 20,7% в 2012 году, т.е. каждый пятый выпускник получил высшее образование в негосударственном вузе.

На рисунке 9 приведены данные о численности выпускников государственных вузов по регионам Центрального федерального округа за исключением г.Москвы и Московской области.

Рис.9. Численность выпускников государственных учреждений высшего профессионального образования в регионах Центрального федерального округа

(2012 год)

Как видим, лидерами по числу выпускников является Воронежская область (22 047 чел.), на втором месте со значительным отставанием - Белгородская область (13 031) и на третьем месте - Ивановская область (9 350). Тверская область находится на 13-м месте опережая только Смоленскую, Калужскую и Костромскую области.

Задание к теме «Средние величины и показатели вариации»

Используя данные Росстата о ценах на продовольственные товары в Центральном федеральном округе (табл.2), средствами MS Excel рассчитайте следующие показатели:

• среднюю цену товара;

• медиану;

• размах вариации;

• среднее линейное отклонение;

• дисперсию;

• среднеквадратичное отклонение;

• коэффициент осцилляции;

• линейный коэффициент вариации;

• коэффициент вариации.

По результатам расчетов сделайте аналитические выводы.

Методические указания по выполнению работы

Исходные данные организуйте на рабочем листе Excel как показано на рисунке 10.

Рис.10. Организация данных на рабочем листе Excel для расчета средних и

показателей вариации

Чтобы рассчитать нужные показатели в Excel необходимо в ячейках задать формулы расчета соответствующих показателей. Формула - это выражение, состоящее из операндов, которое используется для выполнения вычислений над имеющимися данными. Каждая формула начинается с символа равно (=). В качестве операндов могут быть: числа, логические значения, ссылки на адреса ячеек (диапазон ячеек), встроенные функции, которые соединяются с помощью символов операций - сложения, вычитания, умножения, деления, возведения в степень.

Excel выполняет вычисления последовательно, но некоторые операции имеют более высокий приоритет и выполняются раньше других:

1. возведение в степень и выражения в круглых скобках;

2. умножение и деление;

3. сложение и вычитание.

Технические возможности Excel позволяют создавать достаточно сложные формулы. Помимо ввода формул вручную Excel предлагает широкий набор встроенных функций. Существенную помощь в процессе конструирования выражений, содержащих формулы, может оказать Мастер функций, который вызывается через меню Вставка^ Функция.

Копируются формулы так же, как и другие данные. Однако при копировании формулы следует помнить, что они содержат ссылки на другие ячейки. В определенных случаях адреса должны оставаться неизменными, а в других ситуациях требуется, чтобы они перемещались с учетом относительного изменения местоположения формулы. Для решения данной задачи в Excel поддерживается система относительных и абсолютных ссылок. Абсолютная ссылка - это не изменяющийся при копировании и перемещении формулы адрес ячейки, содержащий исходные данные. В качестве признака абсолютной ссылки в адресе используется знак $. Различают:

полную абсолютную ссылку (знак $ ставится и перед именем столбца, и перед номером строки, например $А$8). В этом случае при копировании и перемещении адрес ячейки не меняется;

частичную абсолютную ссылку (знак $ ставится либо перед номером строки, либо перед именем столбца, например А$8 или $А8. В данном случае при копировании и перемещении неизменной остается только одна из координат).

В случае относительных ссылок при копировании и перемещении формул происходит пересчет адресов ячеек, на которых они указывают, с учетом относительного изменения места этих формул на листе. По умолчанию используется относительная адресация.

Расчет среднего значения в Excel можно провести с использованием функции СРЗНАЧ. Чтобы использовать эту функцию вызовите Мастер функций и выберите требуемую функцию. В поле Число 1 задайте ссылки на ячейки, содержащие значения, среднее которых следует вычислить (рис.11).

Рис.11. Функция СРЗНАЧ

Для определения медианы вариационного ряда в Excel предусмотрена статистическая функция МЕДИАНА. В поле Число 1 задается диапазон ячеек, содержащих значения вариационного рядя для которого следует вычислить медиану (рис.12).

Рис.12. Функция МЕДИАНА

Чтобы рассчитать размах вариации предварительно следует определить минимальное и максимальное значение вариационного ряда. В Excel для этого соответственно предназначены функции МИН и МАКС. В поле Число 1 указывается ссылка на ячейки со значениями, для которых определяется минимум (максимум) (рис.13).

Рис.13. Функция МИН

После этого определяется размах вариации - формула записывается вручную. Начиная со знака «=», далее указывается ссылка на ячейку с максимальной ценой, ставится знак «-» и, указывается ссылка на ячейку с минимальной ценой.

Чтобы вычислить среднее линейное отклонение требуется провести промежуточные расчеты. Удобнее всего это сделать, используя вспомогательную таблицу (рис.14).

Н

G

вспомогательная га&лнца

Рис. 14. Вспомогательная таблица для расчета среднего линейного отклонения

Расчет отклонения фактического значения показателя от среднего производится с использованием относительной ссылки на ячейки, содержащие фактическое значение и абсолютной ссылки на ячейку, содержащую среднее значение показателя (=B3-E$3).

Модуль числа в Excel вычисляется при помощи встроенной функции ABS. В поле Число 1 указывается ссылка на ячейку, содержащей значение, модуль которого следует вычислить (рис.15).

Рис.15. Функция ABS

Чтобы суммировать значения можно воспользоваться функцией СУММ. В поле Число 1 выделить диапазон ячеек, значения которых следует сложить (рис.16).

Рис.16. Функция СУММ

Далее формула для расчета среднего линейного отклонения конструируется вручную (=H20/17).

Вычисление дисперсии в Excel осуществляется с использованием встроенной функции ДИСП. В поле Число 1 задается диапазон ячеек, дисперсию значений которых следует рассчитать (рис.17).

Рис.17. Функция ДИСП

Для расчета среднеквадратичного отклонения применяется функция СТАНДОТКЛОН. В поле Число 1 задается диапазон ячеек, содержащих данные стандартное отклонение которых требуется вычислить (рис.18).

Рис.18. Функция СТАНДОТКЛОН

Формулы для вычисления коэффициента осцилляции, линейного коэффициент вариации и коэффициент вариации задаются вручную: коэффициент осцилляции =E5/E3*100; линейный коэффициент вариации =E6/E3*100; коэффициент вариации =E8/E3*100.

Ниже приведен рабочий лист Excel с записанными формулами для вычисления требуемых показателей.