Файл: Лабораторная работа по дисциплине Системный анализ и принятие решений Фамилия Горовая Имя Ольга.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 149
Скачиваний: 19
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Лабораторная работа
по дисциплине:
«Системный анализ и принятие решений»
Фамилия: Горовая
Имя: Ольга
Отчество: Анатольевна
Группа №: ИБ-05з
Зачетная книжка: 2010201
Проверил:______________
Санкт-Петербург
2023
Задание 1.1: Исследование амплитудного фильтра
Имеется канал связи, передатчик и приемник сообщений, представленных временной последовательностью амплитудных значений сигнала. Иллюстрация сигнала сообщения, посланного передатчиком на приемник, представлена на рис. 1.1.
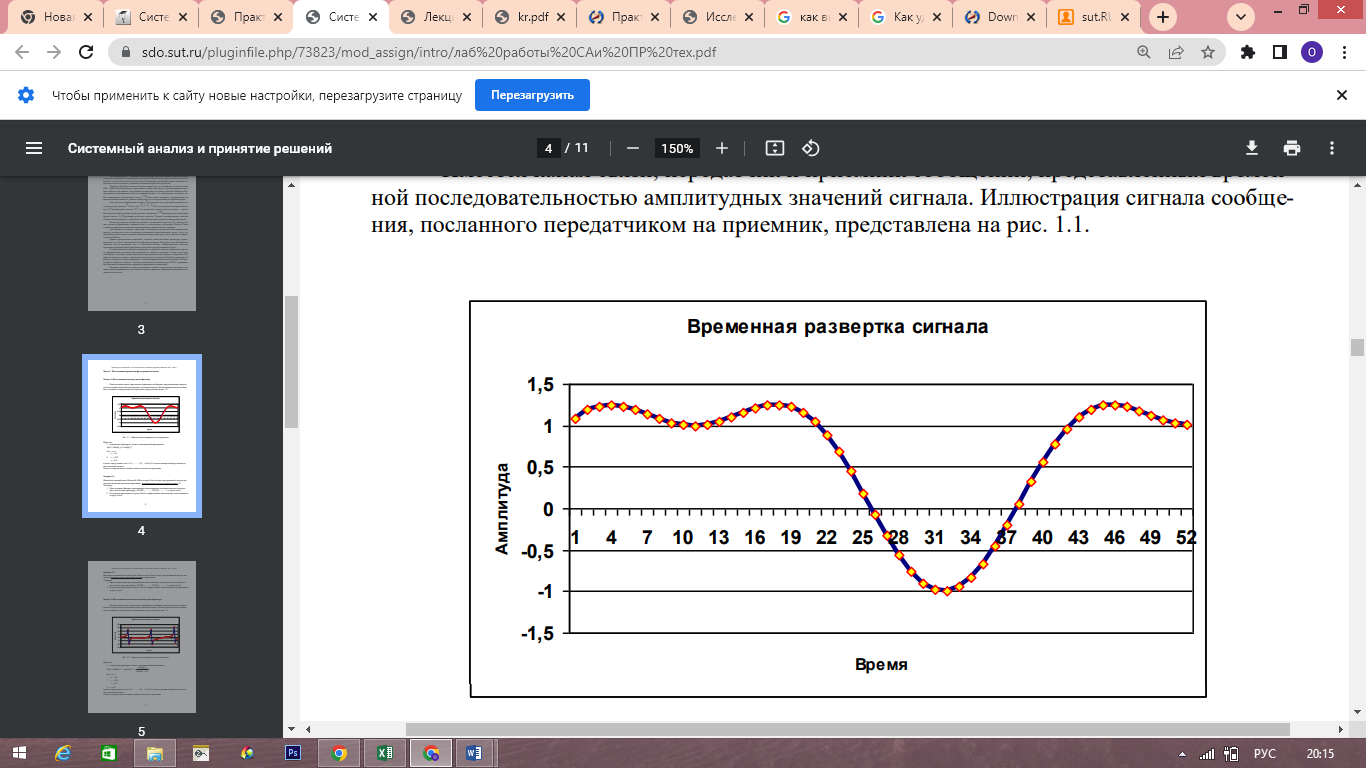
Рис. 1.1 Форма сигнала принятого на приемнике
Известно: 1. передатчик формирует сигнал, описываемый выражением:
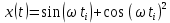
Где: =1
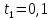
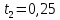
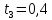
и далее, при условии, что i=1,2,………,52, , а t=0,15 создать дискретный ряд амплитудных значений сигнала.
Сигнал с передатчика по каналу связи поступает на приемник.
Используя типовой пакет Microsoft Office в среде Excel создать программный модуль выделения значений сигнала на приемнике, превышающих амплитудный уровень 1,0.
Указание. 1. При создании фильтра, выделяющего максимальные значения сигнала, использовать логическую процедуру «ЕСЛИ ………., ТОГДА ……….» в среде Excel 2. Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
Решение:
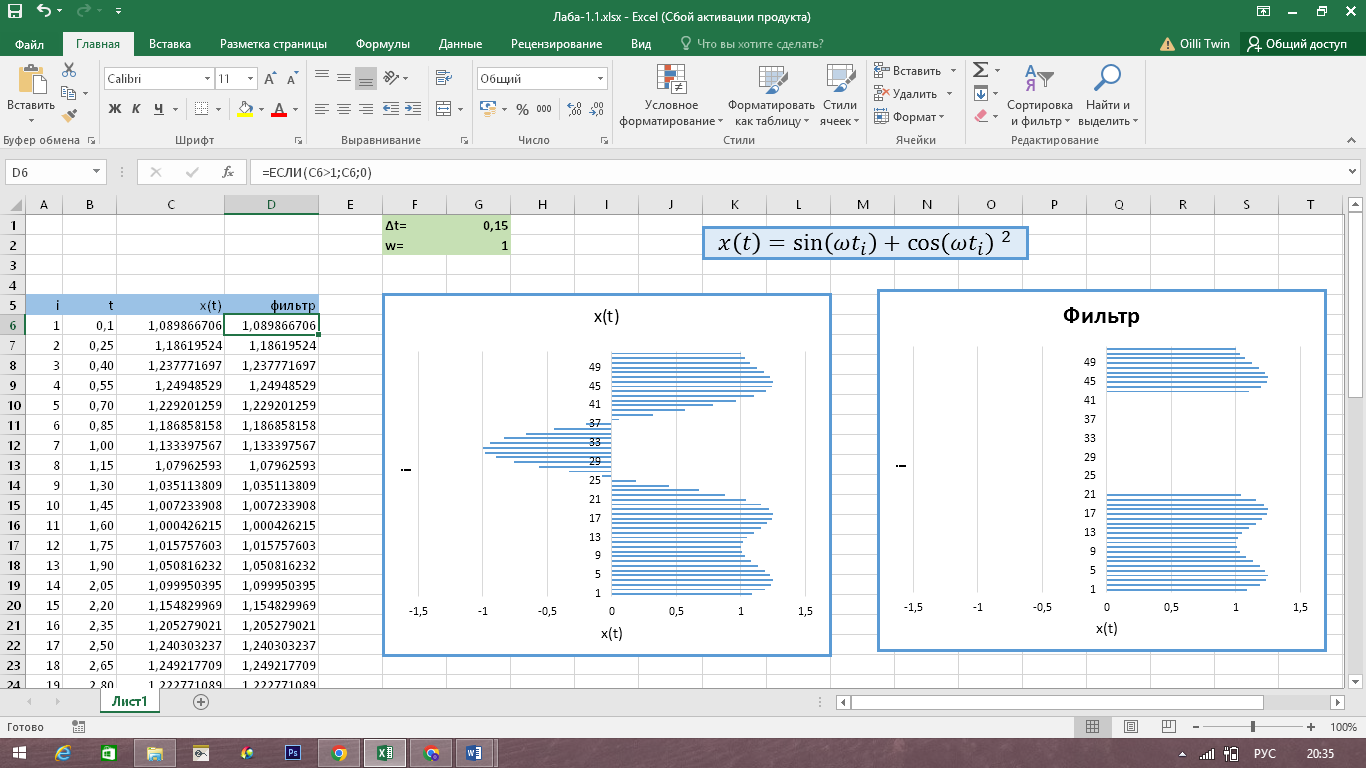
В среде Excel создадим таблицу из четырех столбцов: i, t, x(t) и «фильтр», где i- индексы, принимающие значения от 1 до 52, t- значения коэффицента
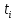, для каждого i; x(t)- значения фунуции x(t) для каждого 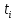, а «фильтр»- столбец, дублирующий все значения x(t)>0 и сопоставляющий 0 остальным значениям x(t)<=0 с помощью логической процедуры «ЕСЛИ..., ТОГДА...».Из данных в столбцах x(t) и «фильтр» создадим график «x(t)», содержащий дискретный ряд всех амплитудных значений сигнала, и график «фильтр», содержащий дискретный ряд только тех амплитудных значений сигнала, которые больше, чем 1.
Тем самым, с помощью графика «фильтр» стало возможно наглядно увидеть значения сигнала на приемнике, превышающие амплитудный уровень 1,0.
Задание 2.1.: Исследование полосового амплитудного фильтра
Имеется канал связи, передатчик и приемник сообщений, представленных временной последовательностью амплитудных значений сигнала. Иллюстрация сигнала сообщения, посланного передатчиком на приемник, представлена на рис. 2.1.
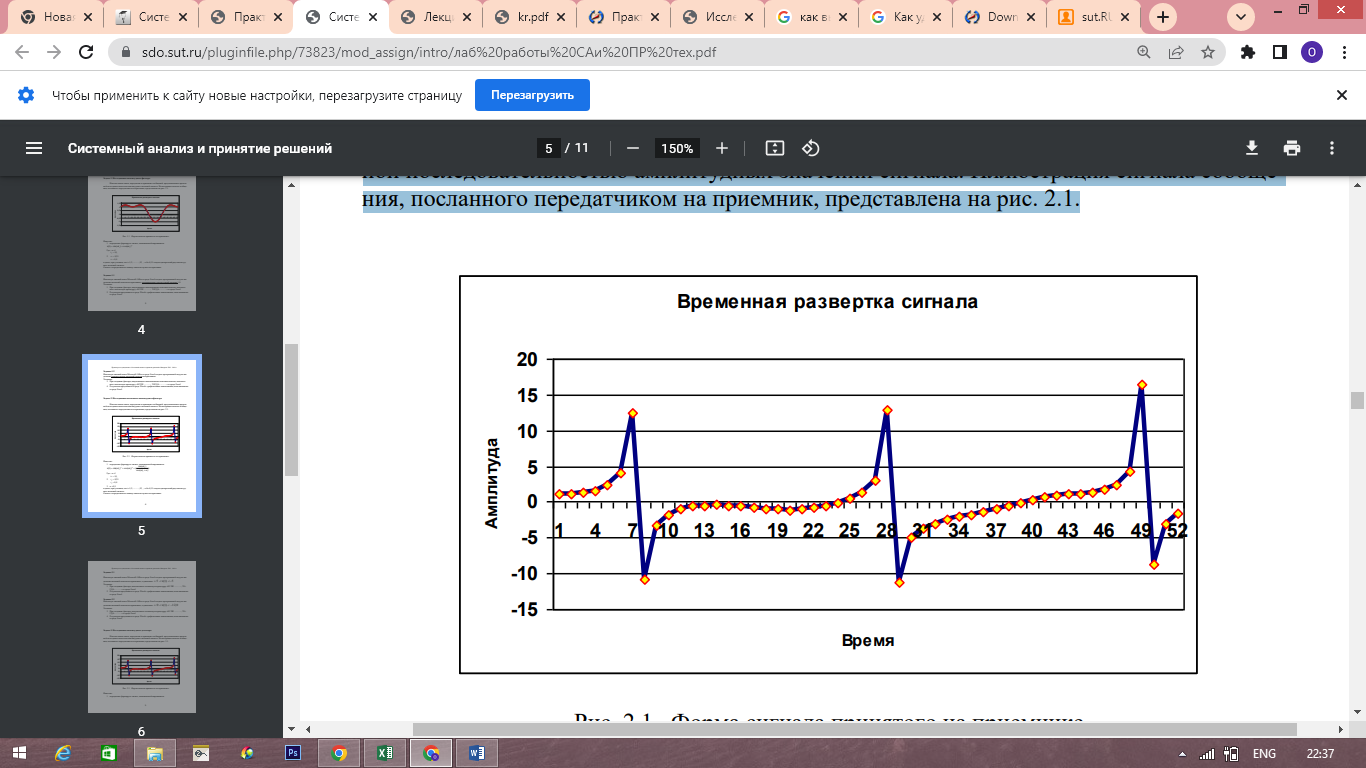
Рис. 2.1 Форма сигнала принятого на приемнике
Известно: 1. передатчик формирует сигнал, описываемый выражением:
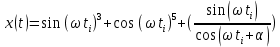
Где: =1
2.
3.
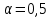
и далее, при условии, что i=1,2,………,52, , а t=0,15 создать дискретный ряд амплитудных значений сигнала. Сигнал с передатчика по каналу связи поступает на приемник.
Используя типовой пакет Microsoft Office в среде Excel создать программный модуль выделения значений сигнала на приемнике, а диапазоне 5 < x(t) < -5 Указание. 1. При создании фильтра, использовать логическую процедуру «ЕСЛИ ………., ТОГДА ……….» в среде Excel 2. Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
Решение:
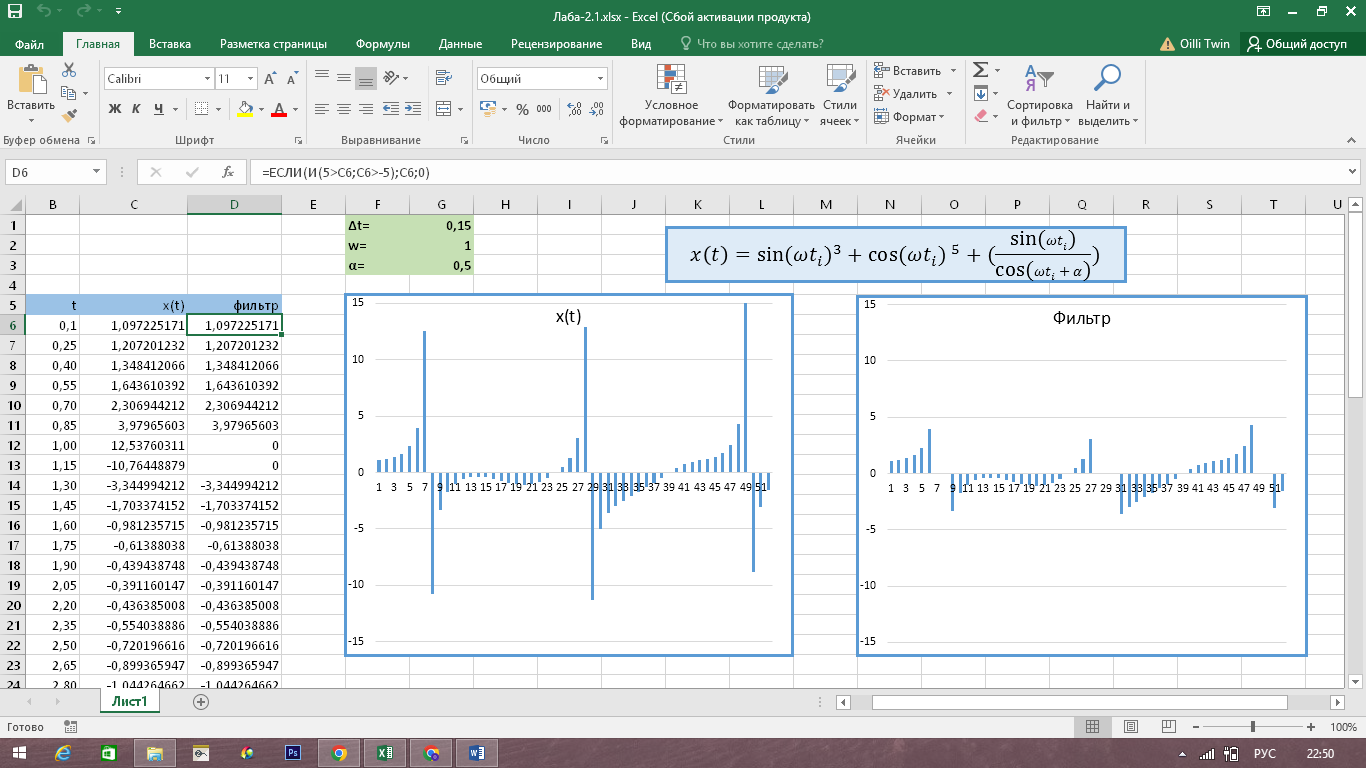
В среде Excel создадим таблицу из четырех столбцов: i, t, x(t) и «фильтр», где i- индексы, принимающие значения от 1 до 52, t- значения коэффицента
, для каждого i; x(t)- значения фунуции x(t) для каждого , а «фильтр»- столбец, дублирующий все значения -5Из данных в столбцах x(t) и «фильтр» создадим график «x(t)», содержащий дискретный ряд всех амплитудных значений сигнала, и график «фильтр», содержащий дискретный ряд только тех амплитудных значений сигнала, которые больше, чем -5, но меньше чем 5.
Тем самым, с помощью графика «фильтр» стало возможно наглядно увидеть значения сигнала на приемнике, находящиеся в диапазоне -5
Задача 3.1. :Исследование амплитудного детектора
Имеется канал связи, передатчик и приемник сообщений, представленных временной последовательностью амплитудных значений сигнала. Иллюстрация сигнала сообщения, посланного передатчиком на приемник, представлена на рис. 3.1.
Рис. 3.1 Форма сигнала принятого на приемнике
Известно: 1. передатчик формирует сигнал, описываемый выражением:
Где: =1
2.
3.
и далее, при условии, что i=1,2,………,52, , а t=0,15 создать дискретный ряд амплитудных значений сигнала. Сигнал с передатчика по каналу связи поступает на приемник.
Используя типовой пакет Microsoft Office в среде Excel создать программный модуль выделения максимальных значений сигнала на приемнике, а диапазоне 2,0 > x(t) > -2,0
Указание. 1. При создании фильтра – детектора , использовать логическую процедуру «ЕСЛИ ………., ТОГДА ……….» в среде Excel 2. Результаты представить в среде Word с графическими пояснениями, исполненными в среде Excel.
Решение:
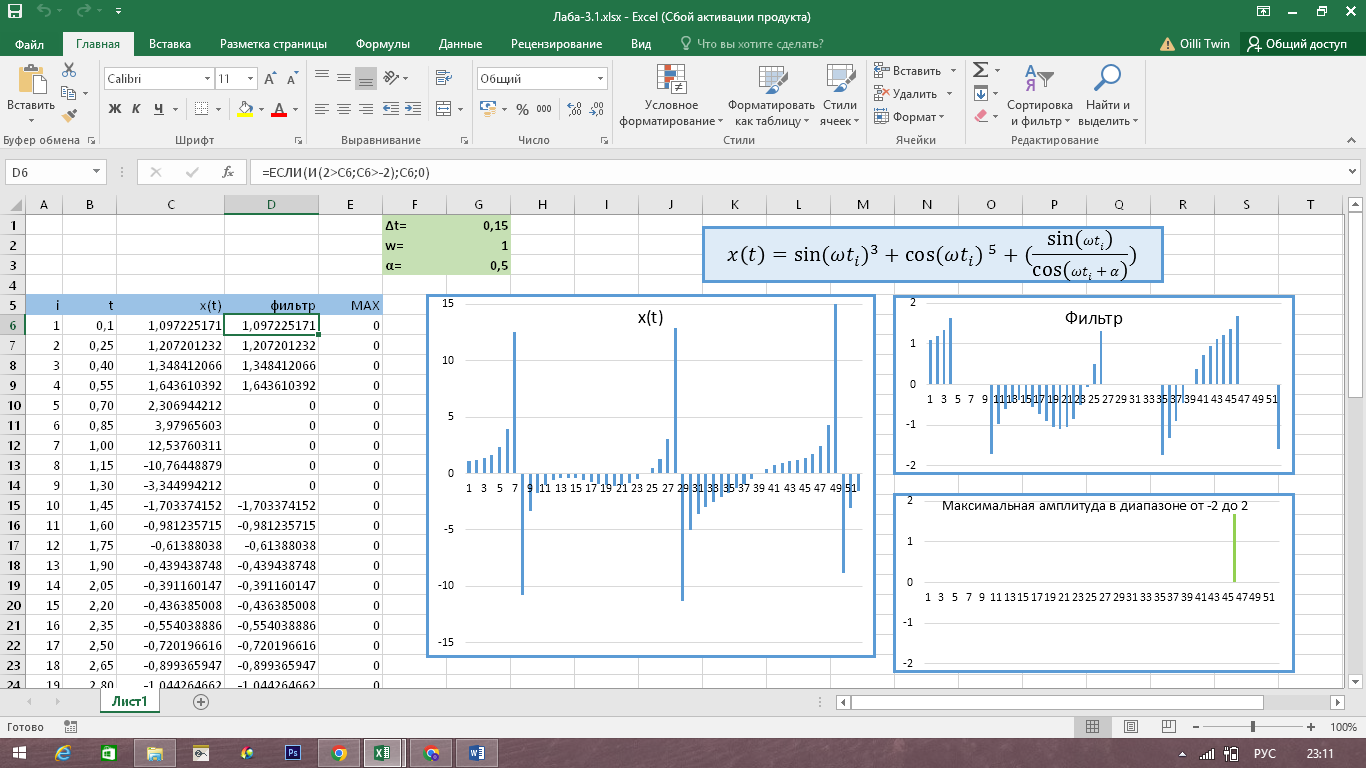
В среде Excel создадим таблицу из пяти столбцов: i, t, x(t), «фильтр» и «MAX», где i- индексы, принимающие значения от 1 до 52, t- значения коэффицента
, для каждого i; x(t)- значения фунуции x(t) для каждого , «фильтр»- столбец, дублирующий все значения -2Из данных в столбцах x(t), «фильтр» и MAX создадим график «x(t)», содержащий дискретный ряд всех амплитудных значений сигнала, график «фильтр», содержащий дискретный ряд только тех амплитудных значений сигнала, которые больше, чем -2, но меньше чем 2, и график «MAX», отображающий максимальные значения x(t) в диапазоне (-2;+2) (на графие видно, что такое значение принимает сигнал, в момент t46).
Тем самым, с помощью графика «MAX» стало возможно наглядно увидеть в какие моменты времени амплитуда сигналов принимает максимальное значение в диапазоне от -2 до +2.
Задача 4. Формирование оценки выборки сигнала
4.1:
В десяти независимых измерениях температуры процессора, установленного на компьютере, получены следующие значения:
Вычислить значение выборочной дисперсии по данному распределению выборки (таблица 4.1).
Решение:
Вычислим значеение выборочной дисперсии по формуле:
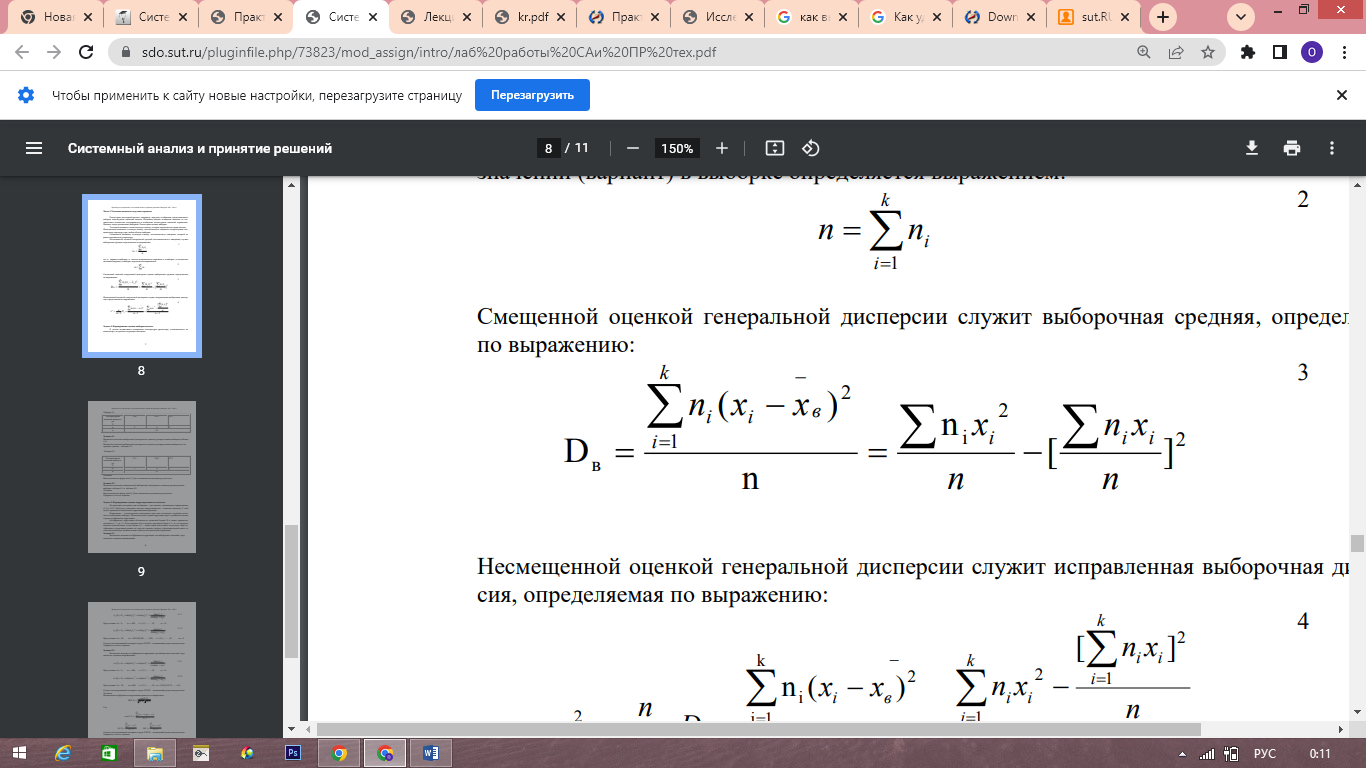
Тогда:
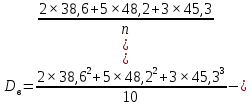
Можем сделать вывод, что значения выборки отдалены от значения математического ожидания в среднем на 13,17 единиц.
Ответ: 13,17
4.2:
Вычислить значение исправленной выборочной дисперсии по данному распределению выборки: таблица 4.1
Решение:
Вычислим значение исправленной выборочной дисперсии по следующей формуле:
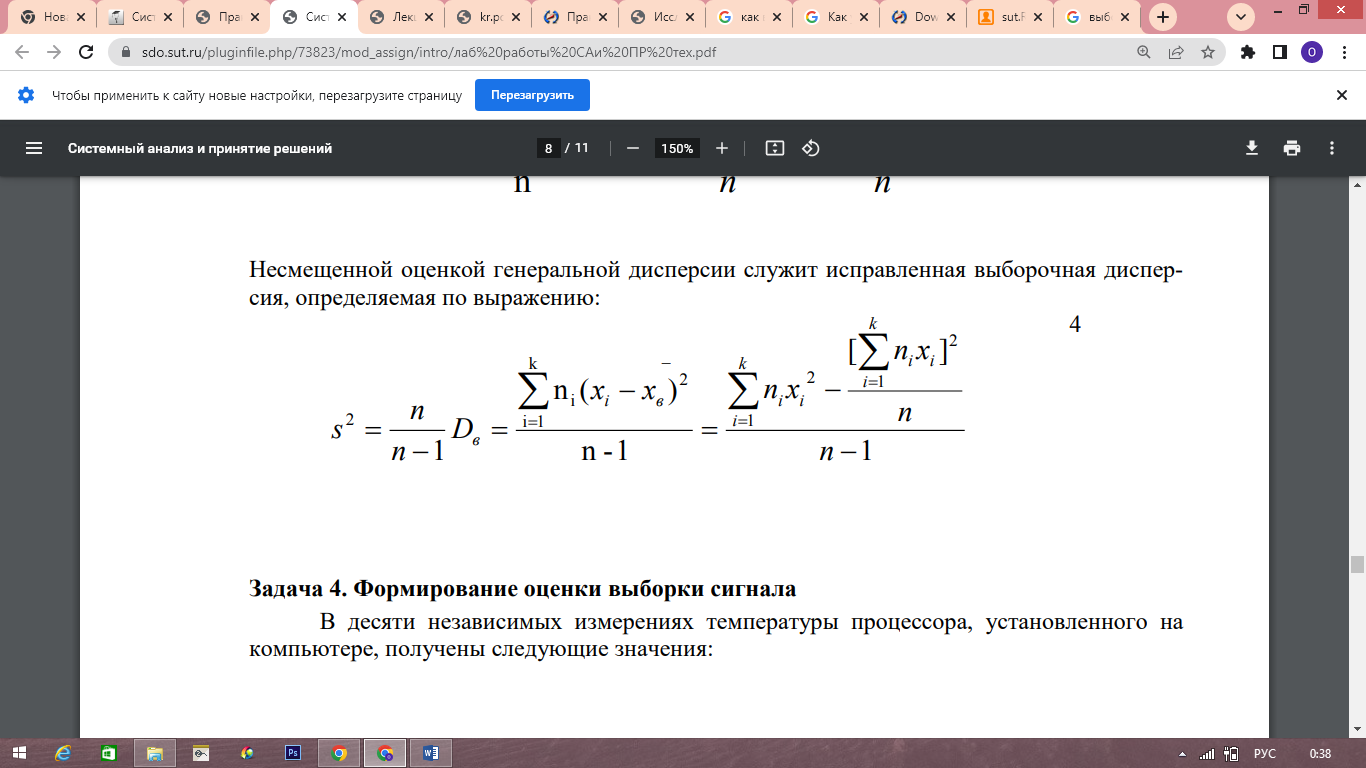
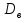нам уже известно, тогда: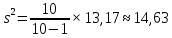
Ответ: 14,63
Задача 5.1. Формирование оценки коррелированности сигналов
На приемник поступают два сообщения – два сигнала, описываемые выражениями (5.1) и (5.2). Требуется установить степень тождественности – схожести сигналов. С этой целью проводится вычисление корреляционной функции. Корреляция — статистическая взаимосвязь двух или нескольких случайных величин, составляющих выборку. Математической мерой корреляции двух случайных величин служит коэффициент корреляции. Коэффициент корреляции обозначается латинской буквой R и может принимать значения от −1 до +1. Если значение R по модулю находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0 — связь слабая или вообще отсутствует. При коэффициенте корреляции равном по модулю единице говорят о функциональной связи, то есть изменения двух величин можно описать математической функцией.
Вычислить значение коэффициента корреляции для выборочных значений двух сигналов, заданных выражениями:
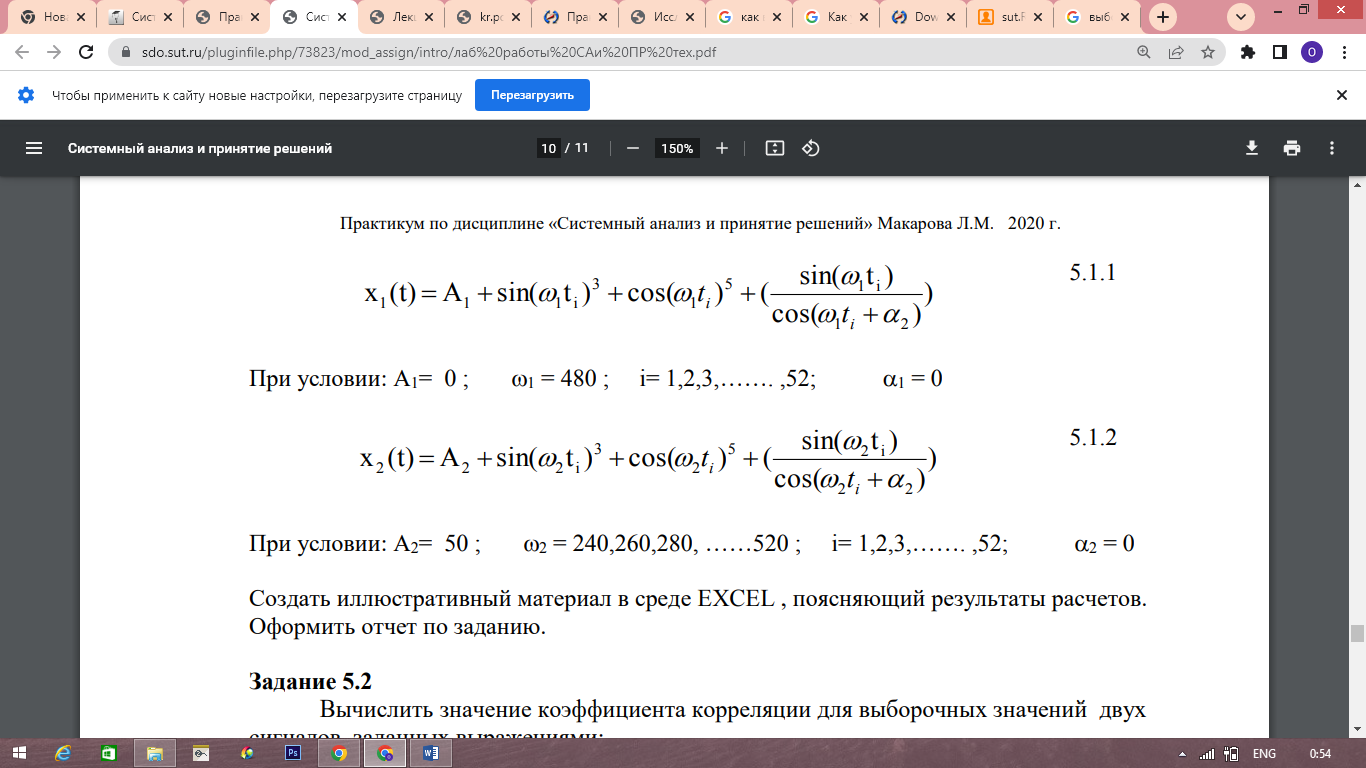
Решение:
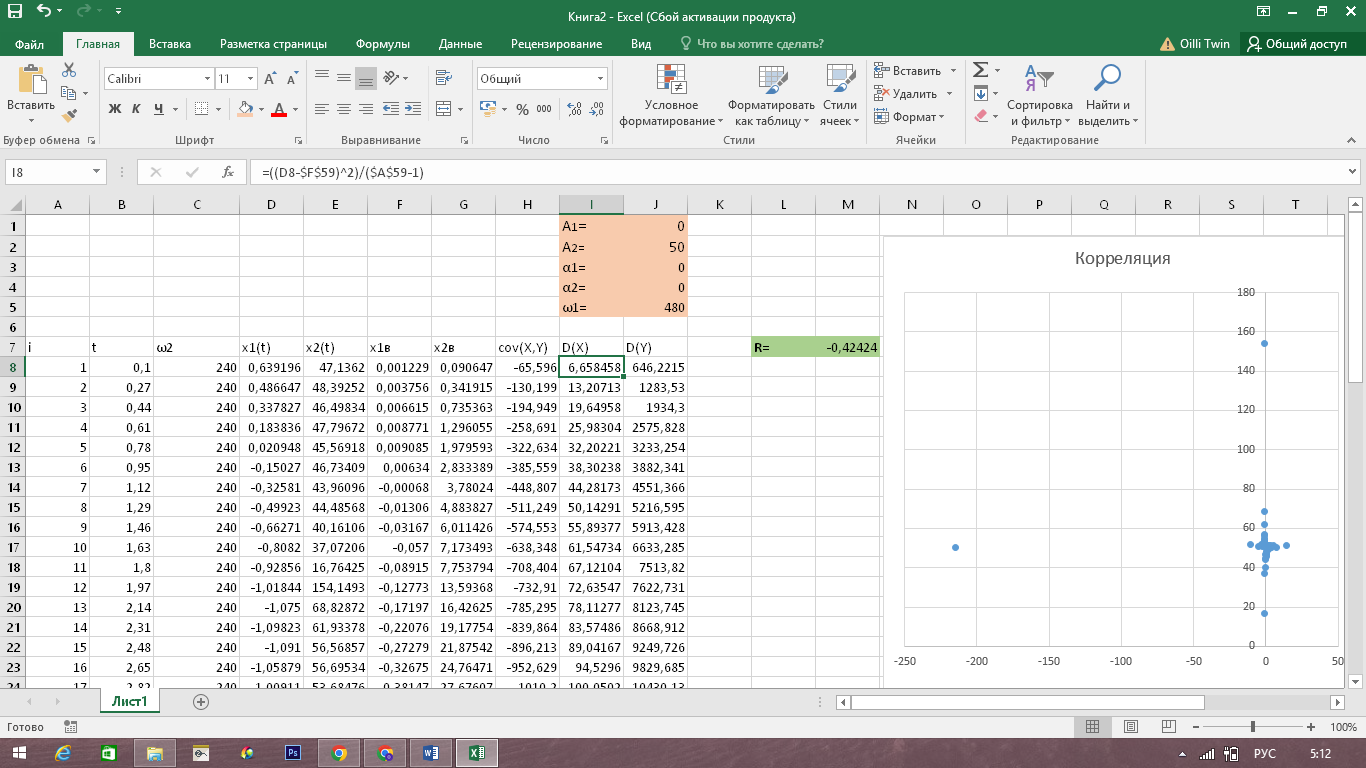
Произведя расчеты по ранее упомянутым формулам в среде Excel, получим значение коэффицента корреляции R= -0,424. Оно свидетельствует о наличии слабой корреляционной связи между значениями двух сигналов.