Файл: Отчет по практической работе 9 по дисциплине Информатика и программирование.docx
Добавлен: 08.11.2023
Просмотров: 64
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего образования «Южно-Уральский государственный университет»
(национальный исследовательский университет)
Высшая школа электроники и компьютерных наук
Кафедра «Информационно-измерительная техника»
Логические основы ЭВМ
ОТЧЕТ
по практической работе №9
по дисциплине «Информатика и программирование»
Выполнил:
студент группы П–172
/ И.Э. Шафиков /
(подпись)
«» г.
Проверил: доцент
/ Н.Ю. Аверина/
(подпись)
«» г.
Практическая работа №9 Логические основы ЭВМ
Цель работы: Научиться строить простейшие логические схемы
Вариант 26.
Задание 1
Для своего варианта таблицы истинности (26) записать:
Решение:
Данная таблица истинности:
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Совершенный ДНФ (СДНФ):
Правила построения СДНФ по таблице истинности: Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Выделим часть таблицы истинности с положительным значением функции:
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
Получившиеся выражение:
(̄x1 ʌ x2 ʌ x3) v (x1 ʌ ˉx2 ʌ ̄x3) v (x1 ʌ ˉx2 ʌ x3) v (x1 ʌ x2 ʌ ˉx3)
-
Совершенные ДНФ и КНФ
| X2 | X1 | X0 | F(x2,x1,x0 | СДНФ | СКНФ |
| 0 | 0 | 0 | 0 | - | x2+x1+x0(x2 v x1 v x0) |
| 0 | 0 | 1 | 1 | 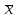 2+ 2+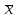 1+x0( 1+x0(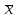 2^ 2^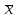 1^x0) 1^x0) | - |
| 0 | 1 | 0 | 1 | 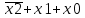 ( (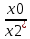 ) ) | - |
| 0 | 1 | 1 | 1 | 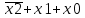 ( (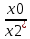 ) ) | - |
| 1 | 0 | 0 | 0 | - | X2+ 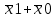 (X2 (X2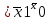 ) ) |
| 1 | 0 | 1 | 0 | - | 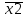 +x1+ +x1+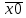 ( (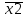 v x1 v v x1 v 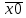 ) ) |
| 1 | 1 | 0 | 0 | - | 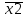 +x1+ +x1+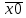 ( (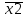 v x1 v v x1 v 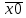 ) ) |
| 1 | 1 | 1 | 1 | 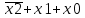 ( (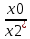 ) ) | - |
-
Минимизация полученных СДНФ и СКН
Минимизация методом непосредственных преобразований ДНФ и КНФ проходит согласно следующим правилам:

Согласно данным правилам минимизируем СДНФ:
(̄x1 ʌ x2 ʌ x3) v (x1 ʌ ˉx2 ʌ ̄x3) v (x1 ʌ ˉx2 ʌ x3) v (x1 ʌ x2 ʌ ˉx3)
↓
(̄x1 ʌ x2 ʌ x3) v(x1 ʌ ˉx2) v (x1 ʌ x2 ʌ ˉx3)
↓
(̄x1 ʌ x2 ʌ x3)v (x1 ʌ ˉx2)v (x1 ʌ ˉx3)
Аналогично минимизируем СКНФ:
(x1 v x2 v x3) ʌ (x1 v x2 v ̄x3) ʌ (x1 v ˉx2 v x3) ʌ (̄x1 v ̄x2 v ˉx3)
↓
(x1vx2) ʌ (x1v ˉx2vx3) ʌ (̄x1v ̄x2v ˉx3)
↓
(x1 v x2 v x3)ʌ(̄x1 v ̄x2 v ˉx3)
↓
̄x1ʌx2 ʌ x3vx1 ʌ ̄x2vx1 ʌ ˉx3
Карта Карно для СДНФ:
| X1\X2X3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Выделим на карте Карно прямоугольные области из единиц наибольшей площади, являющиеся степенями двойки и выпишем соответствующие им конъюнкции:
Область 1:
| X1\X2X3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
K1:x1 ̄x2
Область 2:
| X1\X2X3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
K2: x1 ˉx3
Область 3:
| X1\X2X3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
K3: ̄ x1x2x3
Объединим их с помощью операции ИЛИ и получим минимизированную ДНФ:
X1 ̄x2 vx1 ˉx3 v ̄ x1 x2 x3
Карта Карно для СКНФ:
| X1\X2X3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Выделим на карте Карно прямоугольные области из единиц наибольшей площади, являющиеся степенями двойки и выпишем соответствующие им конъюнкции:
Область 1:
| X1\X2X3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
K1: x1 ̄x2
Область 2:
| X1\X2X3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
K2: x1 ˉx3
Область 3:
| X1\X2X3 | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
K3: ̄ x1 x2 x3
Объединим их с помощью операции ИЛИ и получим минимизированную ДНФ:
̄ x1 ʌ x2 ʌ x3 vx1 ʌ ̄x2 vx1 ʌ ˉx3
На контрольные вопросы:
Вопрос1: Что такое ДНФ и КНФ логические функции и что они собой представляют?
Ответ: Дизъюнкти́вная норма́льная фо́рма (ДНФ)— нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ. Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.
Функцию FF можно задать в форме Крома ⟺⟺ выполнено следующее следствие: F(x1,…,xn)=F(y1,…,yn)=F(z1,…,zn)=1⇒F(x1,…,xn)=F(y1,…,yn)=F(z1,…,zn)=1⇒ F(⟨x1,y1,z1⟩,⟨x2,y2,z2⟩,…,⟨xn,yn,zn⟩)
Вопрос 2
Что такое СДНФ и СКНФ логические функции и что они собой представляют?
Ответ:
Соверше́нная дизъюнкти́вная норма́льная форма — одна из форм представления функции алгебры логики в виде логического выражения. Представляет собой частный случай ДНФ, удовлетворяющий следующим трём условиям: в ней нет одинаковых слагаемых; в каждом слагаемом нет повторяющихся переменных.
Соверше́нная конъюнкти́вная норма́льная форма — это такая КНФ, которая удовлетворяет трём условиям: в ней нет одинаковых элементарных дизъюнкций в каждой дизъюнкции нет одинаковых пропозициональных переменных.