ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИМИНИСТЕРСТВО НАУКИ и высшего образования РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждениевысшего образования«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»Кафедра общей и технической физикиОтчет по практической работе №3По дисциплине ФИЗИКАТема:Определение ускорения свободного падения при помощи универсального маятникаАвтор: студент гр. ГНГ-21-2 ______________ Анненкова М.А.(подпись) (Ф.И.О.)ОЦЕНКА: _____________Дата: 19 октября 2021 г.ПРОВЕРИЛ _____________ _________________(должность) (подпись) (Ф.И.О.)Санкт-Петербург 2021 годЦель работы: определить ускорение свободного падения при помощи универсального маятника.Основные теоретические данныеИзмерения ускорения свободного падения выполняются с помощью косвенных методов. Многие из них основаны на использовании формул для периода колебаний математического и физического маятников.Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити.Период колебаний математического маятника 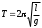, (3.1)где l - длина маятника; g - ускорение свободного падения.Отсюда ускорение свободного падения определяется по формуле 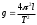(3.2)Ускорение g можно вычислить

---

, измерив Т и l. Погрешность определения g в этом случае связана с тем, что реальный маятник, используемый в лабораторных условиях, может только с некоторым приближением рассматриваться как математический. Чем больше l, тем точнее косвенное измерение ускорения свободного падения с использованием этой методики.

Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести.

Период колебаний физического маятника

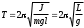, (3.3)

где J - момент инерции маятника относительно оси качаний (точки подвеса); m - его масса; l - расстояние от центра масс до оси качаний.

Величину 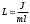называют приведенной длиной физического маятника. Она равна длине такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Зная T, m, lиJ можно по формуле (3.3) найти ускорение свободного падения g. Массу маятника и период его колебаний можно измерить с очень высокой точностью, но точно измерить момент инерции не удается. Указанного недостатка лишен метод оборотного маятника, который позволяет исключить момент инерции из расчетной формулы для g.

Метод оборотного маятника основан на том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за одну или другую, период колебаний его остается одним и тем же.

Расстояние между этими точками представляет собой приведенную длину данного маятника.

Оборотный маятник (рис. 3.1) состоит обычно из металлического стержня А, по которому могут передвигаться и закрепляться в том или ином положении грузы В₁ и В₂ и опорные призмы С₁ и С₂. Центр масс маятника - точка О. Период колебаний маятника можно менять, перемещая грузы или опорные призмы. Маятник подвешивают вначале на призме С₁ и измеряют период его колебаний Т₁. Затем маятник подвешивают на призме С₂ и измеряют период колебаний Т₂.



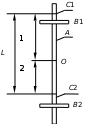
Рис. 3.1. Оборотный маятник. А – металлический стержень, по нему могут передвигаться и закрепляться в том или ином положении грузы

---

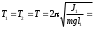
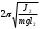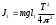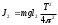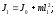
В₁ и В₂ и опорные призмы С₁ и С₂. Точка О – центр масс маятника.Допустим, что нам удалось найти такое положение грузов, при котором периоды колебаний маятников Т₁ и Т₂ на призме С₁ и С₂ совпадают, т.е. . 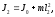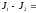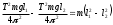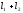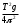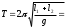(3.4)Отсюда следует, что , (3.5)По теореме Штейнера (3.6)где J₀ - момент инерции маятника относительно оси, проходящей через его центр масс и параллельной оси качаний.С учетом формул (3.5) и (3.6) можно записать .Следовательно = .Период колебаний физического маятника 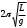(3.7)Ускорение свободного падения 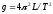(3.8)Формула (3.7) аналогична формуле (1) для математического маятника. Следовательно, L = l₁ + l₂ - приведенная длина физического маятника, которая, как видно из рис.1, равна расстоянию между призмами С₁ и С₂, в момент измерений когда Т₁ = Т₂. 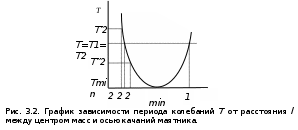Это расстояние легко может быть измерено с большой точностью.Чтобы пояснить процедуру достижения равенства периодов Т₁ и Т₂, исследуем, как зависит период колебаний от расстояния l между центром масс и осью качаний маятника. Согласно формулам (3) и (6), имеем 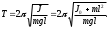(3.9)Для определения минимума функции Т = f(l) (формула 3.9) необходимо приравнять нулю её первую производную. Период колебаний будет минимален т. е. Т = Т_minпри 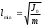(рис. 3.2). При Т  Т_min одно и то же значение Т достигается при двух разных значениях l; одно из них больше, а другое меньше

---

l_min. Эти значения l₁ и l₂ и входят в формулу для приведенной длины маятника L.Вначале измеряется период колебаний маятника Т₁ относительно призмы С₁. Затем маятник переворачивается и измеряется период колебаний Т₂ относительно призмы С₂. Если при этом получится 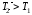, то этому будет соответствовать 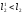. И для того, чтобы приблизить 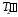и Т₁, надо увеличить 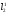. Для этого надо призму С₂ передвинуть от середины стержня к краю. Если получится 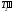< Т₁, то призму С₂ надо будет передвинуть к середине стержня.Анализ точности измерения g методом оборотного маятника показывает, что погрешность измерения слабо зависит от точности, с которой выполняется равенство Т₁ = Т₂. Достаточно добиться того, чтобы периоды оказались равны друг другу с точностью 0,5 %.Кроме того, для получения достаточной точности измерения отношение l₁/l₂ не должно быть слишком малым или слишком большим. 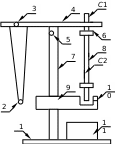Достаточно выполнить изменения в пределах 1,5 < l₁/l₂ < 3.Экспериментальная установкаРис. 3.3. Универсальный маятник. 1 - основание универсального маятника; 2 - математический маятник; 3 – винт; 4 – верхний кронштейн;.5 – винт; 6 – диски; 7 - колонка; 8 - оборотный маятник; 9 - нижний кронштейн; 10 - фотоэлектрический датчик; 11 – секундомер. 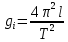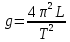С₁ и С₂ – призмы (ножи).Расчетные формулыгде g_i – ускорение свободного падения [м/с²], l – длина математического маятника [м], Т – период колебаний [с]где g – ускорение свободного падения [м/с²], L – приведенная длина оборотного маятника (расстояние между призмами) [м], Т – период колебаний [с]

---

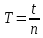
где Т – период колебаний [с], t – время [c], n – количество колебанийПогрешность прямых измеренийΔl=ΔL=0,001 мΔt=0,001 cИсходные данныеl=48 см (длина математического маятника)n=10 (количество колебаний)ТаблицыТаблица 3.1. Математический маятник

Физическая величина	t	Ti	gi
Единицы измерения Номер опыта	с	с	м/с2
1	14,147	1,4147	13,38123418
2	14,141	1,4141	13,38691182
3	14,141	1,4141	13,38691182
4	14,141	1,4141	13,38691182
5	14,140	1,414	13,38785856
6	14,140	1,414	13,38785856
7	14,139	1,4139	13,38880543
8	14,137	1,4137	13,39069958
9	14,138	1,4138	13,38975244
10	14,137	1,4137	13,39069958

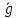=13,38776438 м/с²Таблица 3.2. Оборотный маятник

Физическая величина	t	T1	Tcр1	Т2	g
Единицы измерения Номер опыта	с	с	с	с	м/с2
1	12,894	1,2894	1,2634	1,2772	9,8992
2	12,511	1,2511
3	12,497	1,12497

---

Смотрите также файлы

• Работа с системным реестром.docx

• Лабораторная работа 4 Выбор рационального восстановления детали Выполнил обучающийся Курс 4.docx

• Технология общественного питания.docx

• Правила соревнований в волейболе..docx

• Отчет по практической работе Работа с управляемыми коммутаторами.docx