Файл: Физические основы гемодинамики 34. Жидкости, коэффициент вязкости которых зависит от режима их течения, называются.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 300
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. Допустим, что в двух кровеносных сосудах градиент давления одинаков, а поток крови (объемный расход) во втором сосуде на 80% меньше, чем в первом. Найти отношение их диаметров.
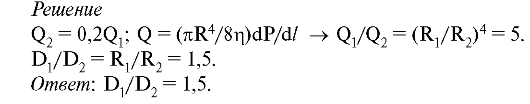4. Какова должна быть разность давлений АР на концах капилляра радиуса r = 1 мм и длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1 см3 воды (коэффициент вязкости η1 = 10-3 Пас) или глицерина (η2 = 0,85 Пас)?
5. Падение давления в кровеносном сосуде длины L = 55 мм и радиуса r = 1,5 мм равно 365 Па. Определить, сколько миллилитров крови протекает через сосуд за 1 минуту. Коэффициент вязкости крови η = 4,5 мПа-с.
6. При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое значение числа Рейнольдса может снизиться до 1160. Определить для этого случая скорость, при которой возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм. Плотность крови равна ρ = 1050 кг/м3, вязкость крови равна η = 5х10-3 Пас.
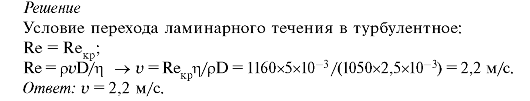7. Средняя скорость крови в аорте радиусом 1 см равна 30 см/с. Выяснить, является ли данное течение ламинарным? Плотность крови ρ = 1,05х103 кг/м3.
η = 4х10-3 Па-с; Rекр = 2300.
8. При большой физической нагрузке скорость кровотока иногда увеличивается вдвое. Пользуясь данными примера задачи (7), определить характер течения в этом случае.
Решение
Re = 2x1575 = 3150. Течение турбулентное.
Ответ: число Рейнольдса больше критического значения, поэтому течение может стать турбулентным.
9. Рассчитать число Рейнольдса для течения крови в капилляре, если скорость течения равна 0,5 мм/с, а диаметр капилляра 0,1 мм. Плотность крови ρ = 1050 кг/м3, η = 4x10-3 Па-с.
10. Определить максимальную массу крови, которая может пройти за 1 с через аорту при сохранении ламинарного характера течения. Диаметр аорты D = 2 см, вязкость крови η = 4x10-3 Па-с.
11. Определить максимальную объемную скорость протекания жидкости по игле шприца с внутренним диаметром D = 0,3 мм, при которой сохраняется ламинарный характер течения.
12. Найти объемную скорость жидкости в игле шприца. Плотность жидкости - ρ; ее вязкость - η; диаметр и длина иглы D и L соответственно; сила, действующая на поршень, - F; площадь поршня - S.
Интегрируя по r, получим:
Пусть поршень шприца движется под действием силы F со скоростью u. Тогда мощность внешней силы NF = Fu.
Суммарная работа всех сил равна изменению кинетической энергии. Следовательно,
Подставив найденное значение AP во второе уравнение, получим все интересующие нас величины: скорость поршня и, объемную скорость кровотока Q, скорость жидкости в игле v.
Биореология. Модели кровообращения
1) Кристаллические и аморфные тела. Полимеры.
2) Механические свойства твердых тел. Деформации (растяжение, сдвиг). Относительное удлинение. Напряжение. Закон Гука.
3) Экспериментальная кривая растяжения. Предел упругости. Предел текучести. Предел прочности.
4) Модель деформации Кельвина-Фойхта.
5) Механические свойства биологических тканей: костной, кровеносных сосудов, мышц.
6) Механическое напряжение стенки кровеносного сосуда
7) Ударный объем крови.
8) Пульсовая волна. Давление в пульсовой волне. Скорость пульсовой волны (формула Моенса-Кортевега).
9) Изменение среднего значения давления и скорости кровотока в зависимости от типа кровеносных сосудов.
10) Работа и мощность сердца.
11) Физические основы клинического метода измерения давления крови.
12) Методы определения скорости кровотока.
1) Кристаллические и аморфные тела. Полимеры.
Кристаллы- твердые тела, атомы или молекулы которых занимают определенные, упорядоченные положения в пространстве.
Аморфные тела- твердые тела, у которых существует ближайший порядок, т.е. некоторый порядок в расположении смежных частиц, который уменьшается с увеличением расстояния.
Полимеры- вещества, молекулы которых представляют собой длинные цепи, составленные из большого числа атомов или атомных группировок, соединенных химическими связями.
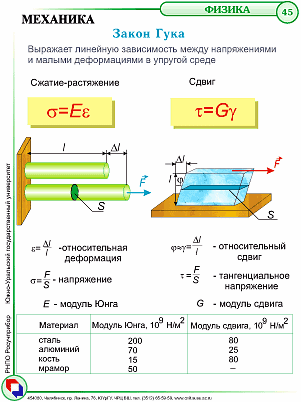
2) Механические свойства твердых тел. Деформации (растяжение, сдвиг). Относительное удлинение. Напряжение. Закон Гука.
Деформация- внешнее механическое воздействие на тело, которое приводит к изменению его объема и/или формы.
Растяжение - вид деформации, которая возникает при действии силы, направленной вдоль оси.
Деформация сдвига- вид деформации, при котором происходит взаимное смещение параллельных слоев материала под воздействием деформирующих сил.
Относительное удлинение-мера деформации растяжения. Равно отношению абсолютного удлинения тела к первоначальной длине.
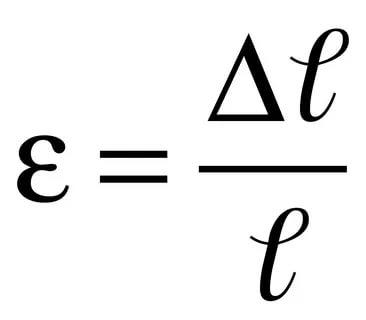
Напряжение-мера внутренних сил, возникающих в деформированном теле под влиянием различных факторов.
-результат взаимодействия частиц тела при его нагружении.
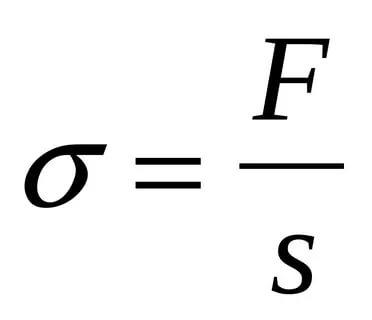
Закон Гука: напряжение пропорционально деформации.
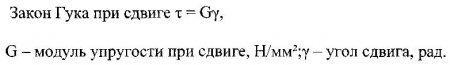
3) Экспериментальная кривая растяжения. Предел упругости. Предел текучести. Предел прочности.
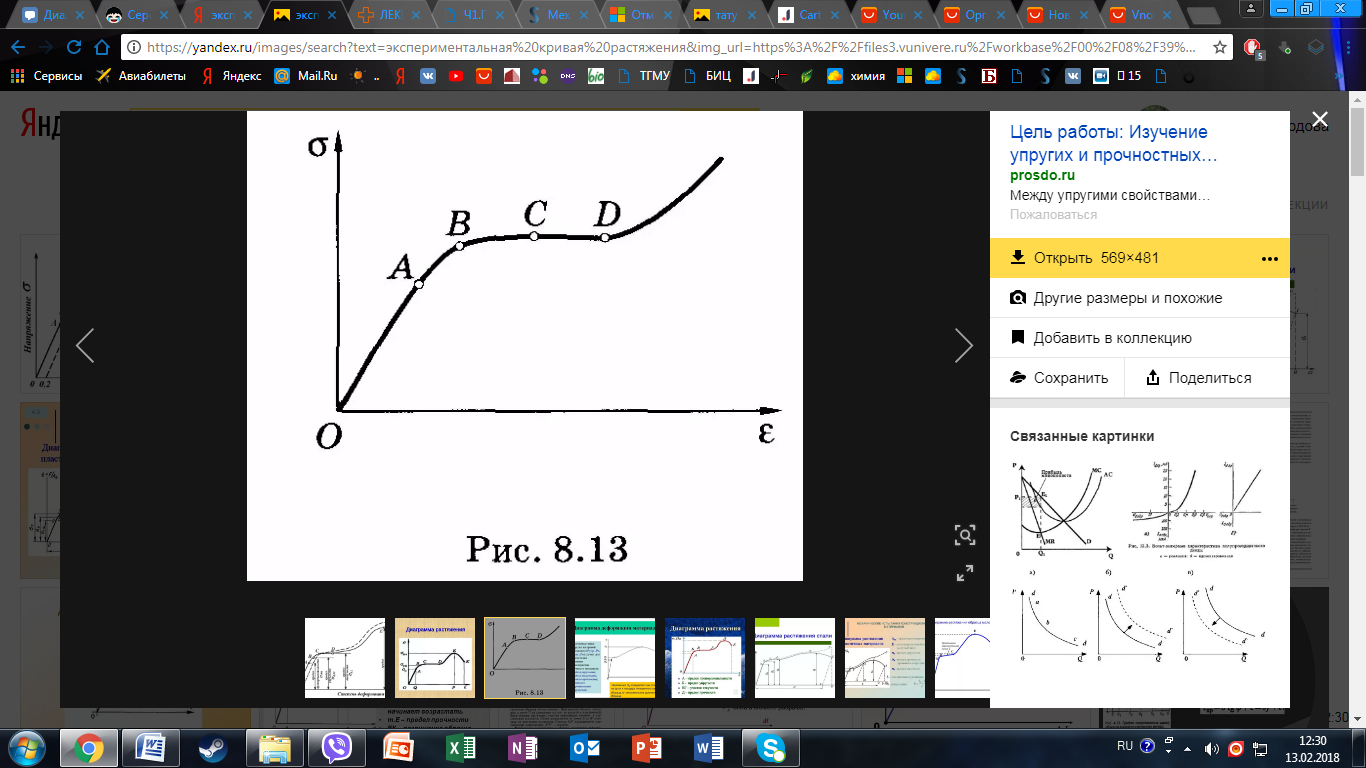Предел упругости- максимальное напряжение, при котором еще не имеют места деформации, остающиеся в теле после снятия напряжения (остаточные деформации).
Предел тякучести- напряжение, с которого деформация возрастает без увеличения напряжения. Предел прочности- напряжение, определяемое наибольшей нагрузкой, выдерживаемой перед разрушением.
ОА-упругие деформации, В-предел упругости, СD-предел тякучести
4) Модель деформации Кельвина-Фойхта.
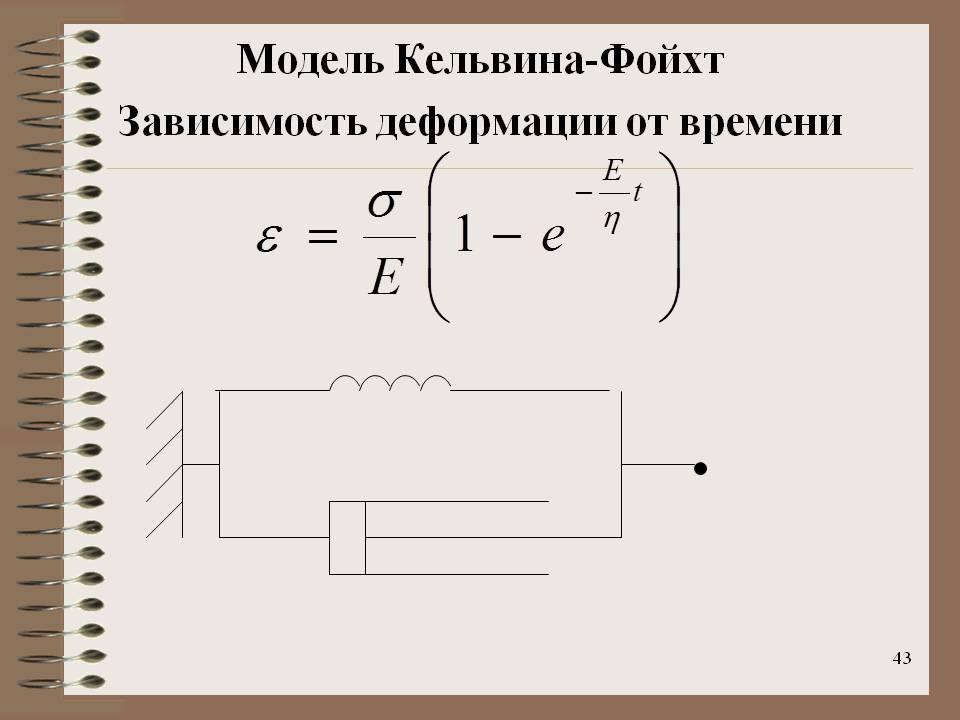
Вязкоупругая модель. Состоит из параллельно соединенных пружины и поршня. Используется, чтобы выявить ползучее поведение полимеров. Деформация экспоненциально возрастает со временем.
5) Механические свойства биологических тканей: костной, кровеносных сосудов, мышц.
Костная ткань.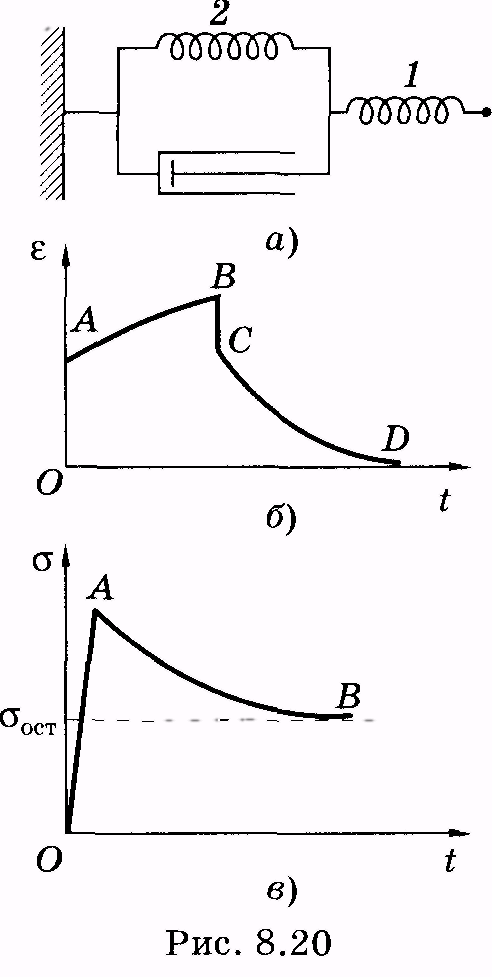
минеральное содержимое кости обеспечивает быструю деформацию, а полимерная часть (коллаген) определяет ползучесть. Если создать быструю деформацию, то возрастает напряжение ОА АВ- напряжение убывает, затем сохраняется остаточное напряжение
Не возникает при постоянной деформации такой ситуации, чтобы пружины вернулись в прежние состояние.
Ткань кровеносных сосудов (сосудистая ткань).
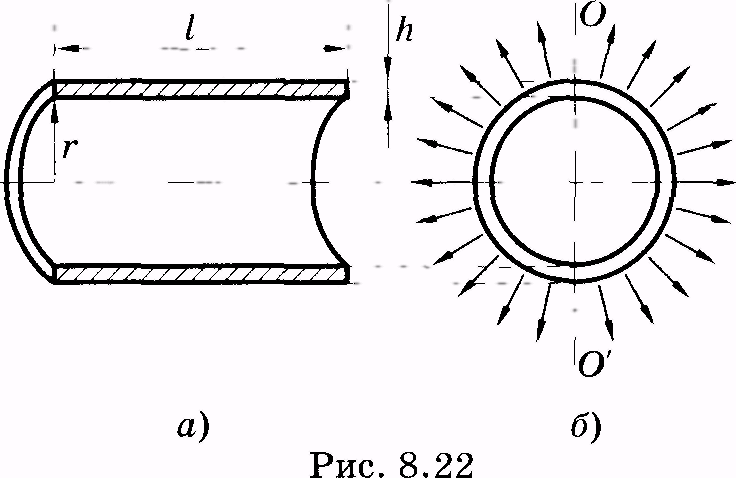
Можно рассматривать деформацию сосуда в целом как результат действия давления изнутри на упругий цилиндр. Две половины сосуда взаимодействуют между собой по сечениям стенок. Общая площадь "сечения взаимодействия" 2hl.
Если в сосудистой стенке существует механическое напряжение σ, то сила взаимодействия двух половинок сосуда равна
F = σ • 2hl.
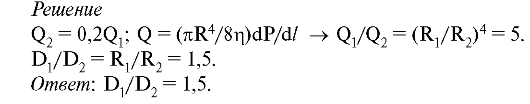4. Какова должна быть разность давлений АР на концах капилляра радиуса r = 1 мм и длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1 см3 воды (коэффициент вязкости η1 = 10-3 Пас) или глицерина (η2 = 0,85 Пас)?| |
5. Падение давления в кровеносном сосуде длины L = 55 мм и радиуса r = 1,5 мм равно 365 Па. Определить, сколько миллилитров крови протекает через сосуд за 1 минуту. Коэффициент вязкости крови η = 4,5 мПа-с. 6. При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое значение числа Рейнольдса может снизиться до 1160. Определить для этого случая скорость, при которой возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм. Плотность крови равна ρ = 1050 кг/м3, вязкость крови равна η = 5х10-3 Пас.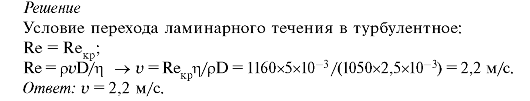 7. Средняя скорость крови в аорте радиусом 1 см равна 30 см/с. Выяснить, является ли данное течение ламинарным? Плотность крови ρ = 1,05х103 кг/м3.η = 4х10-3 Па-с; Rекр = 2300.
8. При большой физической нагрузке скорость кровотока иногда увеличивается вдвое. Пользуясь данными примера задачи (7), определить характер течения в этом случае.
Решение
Re = 2x1575 = 3150. Течение турбулентное.
Ответ: число Рейнольдса больше критического значения, поэтому течение может стать турбулентным.
9. Рассчитать число Рейнольдса для течения крови в капилляре, если скорость течения равна 0,5 мм/с, а диаметр капилляра 0,1 мм. Плотность крови ρ = 1050 кг/м3, η = 4x10-3 Па-с.
10. Определить максимальную массу крови, которая может пройти за 1 с через аорту при сохранении ламинарного характера течения. Диаметр аорты D = 2 см, вязкость крови η = 4x10-3 Па-с.
11. Определить максимальную объемную скорость протекания жидкости по игле шприца с внутренним диаметром D = 0,3 мм, при которой сохраняется ламинарный характер течения. 12. Найти объемную скорость жидкости в игле шприца. Плотность жидкости - ρ; ее вязкость - η; диаметр и длина иглы D и L соответственно; сила, действующая на поршень, - F; площадь поршня - S.| |
Интегрируя по r, получим: Пусть поршень шприца движется под действием силы F со скоростью u. Тогда мощность внешней силы NF = Fu.Суммарная работа всех сил равна изменению кинетической энергии. Следовательно,
Подставив найденное значение AP во второе уравнение, получим все интересующие нас величины: скорость поршня и, объемную скорость кровотока Q, скорость жидкости в игле v.Биореология. Модели кровообращения
1) Кристаллические и аморфные тела. Полимеры.
2) Механические свойства твердых тел. Деформации (растяжение, сдвиг). Относительное удлинение. Напряжение. Закон Гука.
3) Экспериментальная кривая растяжения. Предел упругости. Предел текучести. Предел прочности.
4) Модель деформации Кельвина-Фойхта.
5) Механические свойства биологических тканей: костной, кровеносных сосудов, мышц.
6) Механическое напряжение стенки кровеносного сосуда
7) Ударный объем крови.
8) Пульсовая волна. Давление в пульсовой волне. Скорость пульсовой волны (формула Моенса-Кортевега).
9) Изменение среднего значения давления и скорости кровотока в зависимости от типа кровеносных сосудов.
10) Работа и мощность сердца.
11) Физические основы клинического метода измерения давления крови.
12) Методы определения скорости кровотока.
1) Кристаллические и аморфные тела. Полимеры.
Кристаллы- твердые тела, атомы или молекулы которых занимают определенные, упорядоченные положения в пространстве.
Аморфные тела- твердые тела, у которых существует ближайший порядок, т.е. некоторый порядок в расположении смежных частиц, который уменьшается с увеличением расстояния.
Полимеры- вещества, молекулы которых представляют собой длинные цепи, составленные из большого числа атомов или атомных группировок, соединенных химическими связями.
2) Механические свойства твердых тел. Деформации (растяжение, сдвиг). Относительное удлинение. Напряжение. Закон Гука.
Деформация- внешнее механическое воздействие на тело, которое приводит к изменению его объема и/или формы.
Растяжение - вид деформации, которая возникает при действии силы, направленной вдоль оси.
Деформация сдвига- вид деформации, при котором происходит взаимное смещение параллельных слоев материала под воздействием деформирующих сил.
Относительное удлинение-мера деформации растяжения. Равно отношению абсолютного удлинения тела к первоначальной длине.
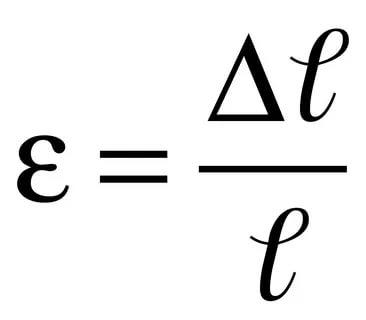
Напряжение-мера внутренних сил, возникающих в деформированном теле под влиянием различных факторов.
-результат взаимодействия частиц тела при его нагружении.
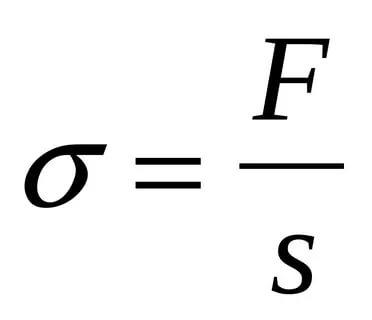
Закон Гука: напряжение пропорционально деформации.
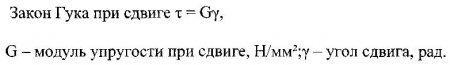
3) Экспериментальная кривая растяжения. Предел упругости. Предел текучести. Предел прочности.
Предел упругости- максимальное напряжение, при котором еще не имеют места деформации, остающиеся в теле после снятия напряжения (остаточные деформации).
Предел тякучести- напряжение, с которого деформация возрастает без увеличения напряжения. Предел прочности- напряжение, определяемое наибольшей нагрузкой, выдерживаемой перед разрушением.
ОА-упругие деформации, В-предел упругости, СD-предел тякучести
4) Модель деформации Кельвина-Фойхта.
Вязкоупругая модель. Состоит из параллельно соединенных пружины и поршня. Используется, чтобы выявить ползучее поведение полимеров. Деформация экспоненциально возрастает со временем.
5) Механические свойства биологических тканей: костной, кровеносных сосудов, мышц.
Костная ткань.
минеральное содержимое кости обеспечивает быструю деформацию, а полимерная часть (коллаген) определяет ползучесть. Если создать быструю деформацию, то возрастает напряжение ОА АВ- напряжение убывает, затем сохраняется остаточное напряжение
Не возникает при постоянной деформации такой ситуации, чтобы пружины вернулись в прежние состояние.
Ткань кровеносных сосудов (сосудистая ткань).
Можно рассматривать деформацию сосуда в целом как результат действия давления изнутри на упругий цилиндр. Две половины сосуда взаимодействуют между собой по сечениям стенок. Общая площадь "сечения взаимодействия" 2hl.
Если в сосудистой стенке существует механическое напряжение σ, то сила взаимодействия двух половинок сосуда равна
F = σ • 2hl.