Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная/очно-заочная

ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙПО ДИСЦИПЛИНЕМАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ (ЧАСТЬ 1/1)Группа То20П111СтудентС.Н.ПироговаМОСКВА 2022Задания к практической работе 2.Статистическая обработка данных.Задание 3.Психолог просит супругов проранжировать девять личностных черт, имеющих определяющее значение для семейного благополучия. Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам. Заполните таблицу и, посчитав коэффициент ранговой корреляции Спирмена, ответьте на поставленный вопрос.

Черты личности		Муж	Жена
Ответственность		6	8
Общительность		4	6
Сдержанность		1	2
Выносливость		2	1
Жизнерадостность		3	4
Терпеливость		5	3
Решительность		7	5
Оптимизм	8			7
Надежность	9			9

---

ранг X, dx	ранг Y, dy	(dx - dy) 2
6	8	4
4	6	4
1	2	1
2	1	1
3	4	1
5	3	4
7	5	4
8	7	1
9	9	0
45	45	45

Проверка правильности составления матрицы на основе исчисления контрольной суммы:Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.По формуле вычислим коэффициент ранговой корреляции Спирмена.Согласованность между мнениями супругов сильная и прямаяЗадание 2.Были протестированы две группы студентов. Тест содержал 60вопросов. Указано число правильных ответов каждого участника теста.Можно ли утверждать, что одна из групп превзошла другую группу порезультатам теста?Группа 1: 55, 45, 42, 40Группа 2: 46, 41, 38, 35, 34Решение.Проранжируем представленную таблицу. При ранжировании объединяем две выборки в одну. Ранги присваиваются в порядке возрастания значения измеряемой величины, т.е. наименьшему рангу соответствует наименьший балл. Заметим, что в случае совпадения баллов для нескольких учеников ранг такого балла следует считать, как среднее арифметическое тех позиций, которые занимают данные баллы при их расположении в порядке возрастания.Используя предложенный принцип ранжирования, получим таблицу рангов.X Ранг X Y Ранг Y34 0 35 40 38 42 41 45 46 55

---

Сумма 0 Сумма 0Этих данных достаточно, чтобы воспользоваться формулой расчёта эмпирического значения критерия:uemp=5*5+ 5(25+1) - 0=40Гипотеза H0 о незначительности различий между выборками принимается, если Uкр < uэмп. В противном случае H0 отвергается и различие определяется как существенное.где Ukp - критическая точка, которую находят по таблице Манна-Уитни.Найдем критическую точку Ukp.По таблице находим Ukp(0.05) = 9По таблице находим Ukp(0.01) = 4Так как Ukp < uэмп — принимаем нулевую гипотезу с вероятностью 95%; различия в уровнях выборок можно считать не существеннымиОтвет: Группа 1 не превосходит группу 2 по результатам тестаЗадания к практической работе 1.Определение числовых характеристик.Задание 4.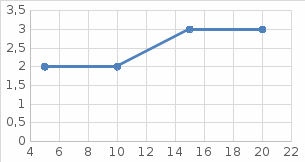Дана выборка: 5,15,15,10,20,20,5,10,20,15. Требуется:а) Построить статистический ряд распределения частот и полигончастот;б) Построить вариационный ряд;в) Найти оценки математического ожидания и дисперсии;г) Найти выборочные моду, медиану, коэффициент вариации,коэффициент асимметрииРешение.Упорядочим значения по возрастанию

5

5

10

10

15

15

15

20

20

20

Найдем количество вхождений каждого значения, получим ряд распределения частот, по которому построим полигон частот.

xi	ni
5	2
10	2
15	3
20	3

Промежуточные вычисления:

xi	ni	xi ni	(xi-X)2 * ni	(xi-X)3 * ni
5	2	10	144,5	-1228,25
10	2	20	24,5	-85,75
15	3	45	6,75	10,125
20	3	60	126,75	823,875
	10	135	302,5	-480

---

Найдем выборочное среднее: X = (1/n) *  x_i n_i = (1/10)*135 = 13,5Найдем исправленную дисперсию (несмещенную оценку длядисперсии по выборке): S² = (1/n-1) *  (x_i-X)² *n_i = (1/9)*302,5  33,611Исправленное среднеквадратичное отклонение: S  5,797Мода – значение с наибольшей частотой: Мо = 20 .Медиана – значение в середине ряда, в данном случае среднееарифметическое двух серединных значений: Ме = (10+15)/2 = 12,5Коэффициент вариации: V = (S/X)*100% = (5,797/13,5)*100%  42,94%Коэффициент асимметрии:As = [ (1/n) *  (x_i-X)²n_i ]/s³ = -48/5,797³  -0,289Задание 1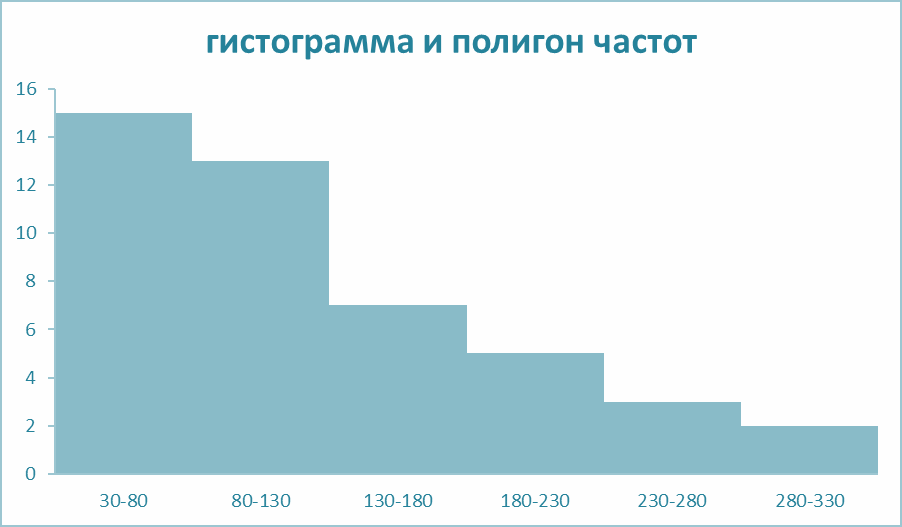Проведено выборочное обследование частных психологическихкабинетов города. Имеются следующие данные о величине посещаемости для50 кабинетов города (xi – количество клиентов в месяц, млн. руб.; ni – числокабинетов).

xi	30-80	80-130	130-180	180-230	230-280	280-330
ni	15	13	7	5	3	2

Найти: а) среднее X, среднеквадратичное отклонение S и коэффициент V; б) построить гистограмму и полигон частот.Решение:Перейдем к простому вариационному ряду, выбирая в качествезначений середины интервалов. Получим:

xi	55	105	155	205	255	305
ni	15	13	7	5	3	2

Найдем необходимые числовые характеристики на основепоследовательных расчетов:

xi	55	105	155	205	255	305	
ni	15	13	7	5	3	2	45
xi ni	825	1365	1085	1025	762	610	5672
(xi-X)2 * ni	75615	5733	5887	31205	49923	64082	232445

---

Среднее: X = (1/n) * ( x_i n_i) = (1/45) * 5672 = 126 Дисперсия: S² = (1/n) *  ((x_i - X)² * n_i) = (1/45) * 232445 = 5165,4Среднеквадратичное отклонение: S =  S²  71,870Коэффициент вариации:V = (S/X) * 100% = (71,870/126) * 100% = 57,03%Б) Строим гистограмму и полигон частот:

---

Смотрите также файлы

• Система воспитания в профессиональном образовании.docx

• Ао нпо автоматики.docx

• Лабораторнаяработа.docx

• Тема Танатологія. Огляд місця події.docx

• Влияние занятий легкой атлетикой на организм.doc