«Решение задач на совместную работу»Цель урока: формирование умений решать текстовые задачи.Задачи урока:

• 
  научить находить способ решения задач на совместную работу с помощью графических схем;
  
• 
  развивать умения анализировать текстовые задачи;
  
• 
  совершенствовать навыки коллективной и самостоятельной работы.
  

Ход урока

1. 
   Актуализация знаний
   

1. 
   Как складывают дроби? Приведите пример.
   
2. 
   Как вычитают дроби? Приведите пример.
   
3. 
   Как умножить две дроби? Приведите пример.
   
4. 
   Как умножить дробь на натуральное число? Приведите пример.
   
5. 
   Как разделить одну дробь на другую? Приведите пример.
   
6. 
   Как разделить дробь на натуральное число? Приведите пример.
   

2. 
   У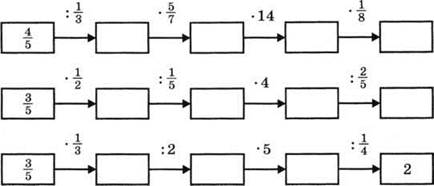 стная работа
   

3. 
   Изучение нового материала
   

1. Задача. Вини Пух съедает банку меда за 3 часа, а его друг Пятачок за 4 часа. За какое время они вдвоем съедят такую банку меда, если будут есть со своей обычной производительностью? (Дети предлагают решение задачи) Решение: Всю работу (съесть целую банку меда) примем за единицу (можно изобразить условие на рисунке). "Производительность" Вини Пуха - 1/3 банки в час. "Производительность" Пятачка - 1/4 банки в час. Общая "производительность" 1/3+1/4=7/12 банки в час. Если предположим, что всю работу, то есть съесть банку меда, они смогут за х часов. Вся работа будет равна производительности, умноженной на время ее выполнения. 1=7\12•х. Отсюда время совместного выполнения работы. 2.Задача. Крокодил Гена, Чебурашка и старуха Шапокляк решили подготовить площадку, на которой они будут строить дом для друзей. Гена, работая один, может выполнить всю работу за 12 часов, Шапокляк – за 15 часов, а Чебурашка – за 20 часов. Какую часть работы каждый из них может выполнить за 1 час? Какую часть работы выполнят они вместе за 1 час. (После обсуждения оформляют решение задачи в виде таблицы) 

	Вся работа	Время	Производительность
Крокодил Гена	1	12 ч	1/12
Чебурашка	1	20 ч	1/20
Шапокляк	1	15 ч	1/15

---

При решении задач на совместную работу «Целое» принимаем за 1; Часть работы за единицу времени – p=1:T, где p-искомая часть работы, T – время работы, а Время работы – T=1:p.Тогда ответим на вопрос задачи:

1. 
   1 : 1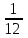2 = (работы) – выполнит Крокодил Гена.
   
2. 
   1 : 20 =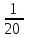 (работы) – выполнит Чебурашка.
   
3. 
   1 : 12 =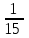 (работы) – выполнит Шапокляк.
   
4. 
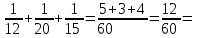
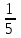   (работы) выполнят вместе.
   
5. 
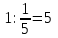   (ч) справятся, работая вместе.
   

Ответ: 5 часов.V. Физкультминутка Раз - подняться, потянуться,Два - нагнуться, разогнуться,Три - в ладоши, три хлопка,Головою три кивка.На четыре - руки шире,Пять - руками помахать,Шесть - на место тихо сесть.VI. Закрепление материалаЗадача №3Три плотника строят дом. Первый плотник один может построить дом  за 2 года,второй  плотник построит дом за 3 года, а третий - за 4 года. Однако строили дом триплотника вместе. За какое  время они построили дом?Решение. При совместной работе складывается не время работы, а часть работы, которую делают ее участники.1 плотник - 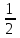всей работы;2 плотник - 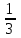всей работы;3 плотник - 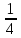всей работы.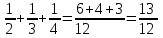 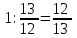годаЗадача №4В городе есть водоем. Одна из труб может заполнить его за 4 часа, вторая – за 8 ч, атретья – за 24 ч. За сколько времени наполнится водоем, если открыть все три трубы?(Учащиеся решают задачу на доске и в тетрадях)VII. Самостоятельная работа1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик -  за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?

---

3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья  - за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.VII. Рефлексия

1. 
   Как решать задачи на совместную работу?
   
2. 
   По какой формуле можно найти время совместной работы?
   
3. 
   Что было самым легким?
   
4. 
   Что было самым трудным?
   
5. 
   Продолжите фразу: “Сегодня на уроке я понял, что…”
   

VIII. Домашнее заданиеНа карточкахПриложение Самостоятельная работа1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик -  за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья  - за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.Самостоятельная работа1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик -  за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья  - за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.Самостоятельная работа1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик -  за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья  - за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.Самостоятельная работа1) Первая бригада может отремонтировать дорогу за 90 дней, а вторая – за 45 дней. За сколько дней могут отремонтировать дорогу обе бригады, работая вместе?

---

2) Фрезеровщик может обработать партию деталей за 3 часа, а его ученик -  за 6 часов. Успеют ли они обработать это количество деталей за 2 часа, если будут работать вместе?3) Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья  - за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.Домашнее задание

1. 
   Старый трактор вспашет поле за 6 часов, а новый за 4 часа. За какое время вспашут поле оба трактора, работая вместе?
   
2. 
   Даша и Маша пропалывают грядку за 12 минут, а одна Маша за 20 минут. За сколько минут пропалывает грядку одна Даша.
   
3. 
   Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья - за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.
   

«3» - решить одну задачу на выбор и придумать одну задачу по теме урока;«4» - решить две задачи на выбор и придумать одну задачу по теме урока; «5» - решить три задачи, придумать одну задачу по теме урока.Домашнее задание

1. 
   Старый трактор вспашет поле за 6 часов, а новый за 4 часа. За какое время вспашут поле оба трактора, работая вместе?
   
2. 
   Даша и Маша пропалывают грядку за 12 минут, а одна Маша за 20 минут. За сколько минут пропалывает грядку одна Даша.
   
3. 
   Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья - за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.
   

«3» - решить одну задачу на выбор и придумать одну задачу по теме урока;«4» - решить две задачи на выбор и придумать одну задачу по теме урока; «5» - решить три задачи, придумать одну задачу по теме урока.Домашнее задание

1. 
   Старый трактор вспашет поле за 6 часов, а новый за 4 часа. За какое время вспашут поле оба трактора, работая вместе?
   
2. 
   Даша и Маша пропалывают грядку за 12 минут, а одна Маша за 20 минут. За сколько минут пропалывает грядку одна Даша.
   
3. 
   Библиотеке нужно переплести книги. Одна мастерская может выполнить эту работу за 16 дней, вторая – за 24 дня, а третья - за 48 дней. В какой срок могут выполнить эту работу три мастерские, работая одновременно.
   

---

«3» - решить одну задачу на выбор и придумать одну задачу по теме урока;«4» - решить две задачи на выбор и придумать одну задачу по теме урока; «5» - решить три задачи, придумать одну задачу по теме урока.

---

Смотрите также файлы

• Отраслям), успешно прошел(ла) учебную практику.pdf

• Проектная деятельность, как способ повышения естественнонаучной грамотности учащихся. (презентация).docx

• Московский государственный областной педагогический университет.docx

• Тактика допроса в конфликтной ситуации.docx

• Аристотель "сомнение приходит после веры " развитая.pdf