1. 
   Теорема Архимеда
   
2. 
   Теорема о предельных переходах в неравенствах
   
3. 
   Теорема о вложенных отрезках
   
4. 
   Теорема Больцано-Вейерштрасса
   
5. 
   Первая теорема Коши
   
6. 
   Вторая теорема Коши
   
7. 
   Первая теорема Вейерштрасса
   
8. 
   Вторая теорема Вейерштрасса
   
9. 
   Теорема Кантера
   
10. 
    Теорема о производных сложной функции
    
11. 
    Теорема о производной обратной функции
    
12. 
    Теорема о параметрически заданной функции
    
13. 
    Теорема Ферма
    
14. 
    Теорема Ролля
    
15. 
    Теорема Лагранжа
    
16. 
    Теорема Коши
    
17. 
    Теорема об остатке формулы Тейлора в форме Пиано
    
18. 
    Теорема о достаточных условиях строгого экстремума
    
19. 
    Теорема о достаточных условиях точки перегиба
    

1. 
   Теорема Архимеда
   

Любая последовательность является неограниченной сверху если для любого действительного числа а существует такое натуральное число n, что n>a.

Док-во (от противного):

Допустим что n ≤ a, т.е. множество натуральных чисел было бы ограничено сверху. Следовательно у N существовала бы конечная верхняя грань.

β(бета) = supN ≤ +∞

Т.к. β-1 < β, то найдется натуральное число n, что n < β-1, т.е. n+1 > β

Но n+1 также натуральное число, поэтому неравенство противоречит условию.

2. 
   Теоремы о предельных переходах
   

Теорема 1:

Пусть последовательность {x_n} сходится. Если начиная с некоторого номера члены последовательности удовлетворяют неравенству x_n ≥ b, то lim x_n ≥ b.

Док-во (от противного):

Пусть lim_n = a. Докажем что a ≥ b.

Пусть a < b. Тогда для любого эпсилон > 0 существует N, такое что для любого n > N => |x_n - a|<эпсилон

Пусть эпсилон = b – a > 0

Тогда из |x_n – a | =>

- b + a < x_n – a < b – a

- b + 2a < x_n < b

Видим противоречие, т.к. x_n ≥ b

Следовательно a ≥ b, lim x_n ≥ b

Следствие:

Пусть { x_n } и { y_n } – сходящиеся последовательности. Если начиная с некоторого номера выполняется неравенство: x_n ≤ y_n, то lim x_n ≤ lim y_n

Док-во: x_n ≤ y_n => y_n - x_n ≥ 0

Lim(y_n - x_n) ≥ 0

Lim y_n

---

– lim x_n ≥ 0

Lim y_n ≥ lim x_n

Теорема 2 (о двух милиционерах):

Пусть сходящиеся последовательности { x_n } и { z_n } имеют один предел, т.е. lim x_n = a и lim z_n = a и начиная с некоторого номера справедливо неравенство x_n ≤ y_n ≤ z_n, тогда последовательность { y_n } сходится к тому же пределу, т.е. lim y_n = a.

Док-во:

Lim x_n = а < = > (знак эквивалентности) для любого эпсилон > 0 существует N1 такое что для любого n > N1 => |xn - a| < эпсилон

Lim z_n = a < = > для любого эпсилон > 0 существует N2 такое что для любого n > N2 => | z_n -a |< эпсилон

N = max { N1, N2 } для любого n > N

a – эпсилон < x_n ≤ y_n ≤ z_n < a + эпсилон

a – эпсилон < y_n < a + эпсилон

- эпсилон < y_n – a < эпсилон

|y_n - a| < эпсилон

Lim y_n = a

3. 
   Теорема о вложенных отрезках
   

Принцип Кантора:

Пусть дана последовательность числовых множеств A_n : A_n+1 < A_n. Такая последовательность – вложенная.

Теорема:

Любая система, такая что A_n+1 < A_n имеет общую точку. Если , то эта точка единственна.

Док-во:

A_n+1 < A_n , A_n = [ a_n, b_n] , a_n – возрастающая последовательность, ограниченная снизу b₁, b_n – убывающая последовательность, ограниченная сверху а₁.

Т.к. a_n < b_n , то по теореме о предельных переходах a ≤ b. Но согласно нашему построению вложенных отрезков a_n ≤ a ≤ b ≤ b_n => [a, b] – общий отрезок для всех отрезков.

0 ≤ b - a ≤ b_n – a_n

=> a = b , и эта точка единственна.

4. 
   Теорема Больцано-Вейерштрасса
   

Теорема:

У любой ограниченной последовательности существует сходящаяся подпоследовательность.

Док-во:

Пусть x_n – ограниченная последовательность, т.е. x_n принадлежит [a, b]

Поделим отрезок [a, b] точкой c => [a, c] и [c, b]. Одно из них бесконечное множество. В бесконечном множестве любое натуральное число обозначим за n1, а в соответствие ему отрезок [a1, b1], т.е. x

---

_n1 принадлежит [a1, b1], x_n2 принадлежит [a2, b2] … x_nk принадлежит [a_k, b_k]. Следовательно, последовательность a_k b_k – вложенная и b_k – a_k = (b – a)/2, при k -> 0.

По теореме о вложенных отрезках получим, что x_nk принадлежит [a_k, b_k] и существует точка c, которая тоже будет принадлежать [a_k, b_k], [x_nk – c] -> 0 и получим что x_nk – искомая последовательность, сходящаяся в точке c.

5. 
   Теорема'>Первая теорема Коши
   

Теорема:

Если функция непрерывна на [a, b] и f(a) * f(b) < 0, то найдется точка c, принадлежащая [a, b], такая что f(c) = 0

Док-во:

Может быть два варианта:

1. 
   f(a) < 0, f(b) > 0
   
2. 
   f(a) > 0, f(b) <0
   

Разделим a, b точкой c пополам:

1. 
   f(c) = 0
   

C - искомая точка

2. 
   f(c) < 0
   

Отрезок (с,b) обозначим как (a,b), полученное делим точкой с напополам. Проведя рассуждения, на каком-то шаге найдем точку, которая является искомой, либо построим отрезок, на котором функция меняет знак.

3. 
   f(c) > 0
   

Построим систему вложенных отрезков [ak, bk]

По принципу Кантера, существует единственная точка с принадлежащая [ak, bk]

Т.к. функция непрерывна на отрезке (a, b), f(ak)->f(c) => Теорема о предельных переходах.

F(bk) -> f(c), причем f(c) ≥ 0

Выполняется только когда F(c) =0

6. 
   Вторая теорема Коши
   

Пусть функция непрерывна на отрезке (а, b), тогда для любых х1,х2 принадлежащих (а, b) существует С, такое что f(x1) ≤ C ≤ f(x2)

Тогда существует C принадлежащее (a, b), такое что f(c) = C

Док-во:

Рассмотрим случай возрастающей функции:

x1 < x2 => f(x1) < f(x2)

C принадлежит [f(x1), f(x2)]

F(x) = f(x) - C

Рассмотрим вспомогательную функцию:

F(x) меняет знак на (х1, х2) и в силу непрерывности функции найдется точка С принадлежащая (х1, х2)

Тогда f(x1) = f(x1) - C < 0

F(x2) = f(x2) - C > 0 => F(x1) * f(x2) < 0

F(x) - непрерывна на промежутке (а, b)

Следовательно существует С, такое что F(c) = 0

Но если f(c)=0

F(c) = f(c) - C = 0

F(c) = C

7. 
   Первая теорема Вейерштрасса
   

Лемма:

Пусть x_n – последовательность со значениями, лежащими на отрезке (a, b) тогда из нее можно выделить сходящуюся последовательность, предел которой принадлежит промежутку (a, b).

---

Теорема:

Если функция непрерывна на (a, b), то она ограничена на этом отрезке.

Док-во:

Предположим функция не ограничена сверху, в силу леммы можно выделить подпоследовательность:

X_nk ----> x₀ (при nk -> 0) => f(x_nk) -> f(x₀) ≥ + ∞

f(x_nk) > n_k ≥ ∞

Следовательно переход к пределу в последнем неравенстве приводит к условию что f(x₀) ≥ + ∞.

Этого быть не может, т.к. f(x₀) – действительное число и f(x₀) < ∞.

8. 
   Теорема:_Если_функция_непрерывна_на_(a,_b),_то_она_достигает_своей_верхней_и_нижней_грани_на_этом_отрезке.Док-во'>Вторая теорема Вейерштрасса
   

Теорема:

Если функция непрерывна на (a, b), то она достигает своей верхней и нижней грани на этом отрезке.

Док-во:

Проведем sup f(x) = s

По первой теореме функция ограничена сверху. Следовательно существует sup f(x) = s, x принадлежит (a, b). Но тогда согласно определению sup:

1. 
   Существует x_n принадлежащая (a, b), f(x_n) > s – (1/n)
   
2. 
   f(x_n) ≤ s
   

9. 
   Теорема Кантора
   

Функция равномерно непрерывна на x если для любого эпсилон > 0 существует дельта > 0, что для любых a, b принадлежащих x из неравенства |a - b| < дельта => неравенство |f(a) – f(b)| < эпсилон.

Теорема:

Если функция непрерывна на (a, b), то она и равномерно непрерывна на нем.

Док-во (от противного):

Пусть для некоторого эпсилон > 0, какое бы дельта > 0 мы ни выбрали, существует два числа a, b принадлежащие x. Для каждого дельта > 0 рассмотрим пару чисел a_n и b_n. Без ограничения общности можно считать последовательность a_n, n принадлежащая N, - сходящейся. Последовательность чисел сходящаяся в точке x₀ => f(a_n) – f(b_n) -> 0, что противоречит предположению.

10. 
    Теорема о производной сложной функции
    

Теорема:

Если y = f(u) и u = ϕ(x) (фи от икс) – дифференцируемые функции, то сложная функция y = f(ϕ(x)) является дифференцируемой функцией и ее производная равна произведению производной данной функции по промежуточному аргументу и производной промежуточного аргумента по независимой переменной: y’ = f’(u) * u’

Док-во:

Утверждение получается из равенства 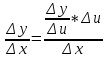(при

---

≠ 0 и 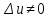) предельным переходом при

11. 
    
    

---

Смотрите также файлы

• Новогодний классный огонек Волшебные часы для учащихся 56 классов Цель мероприятия.docx

• Проверяемое задание Сбор и систематизация технической информации.docx

• Анатомофункциональные особенности сердечнососудистой системы у детей.docx

• Практическое задание к занятию 7.pdf

• Все типы условных предложений состоят из двух частей 1) главной части 2)придаточной (условной) части.ppt