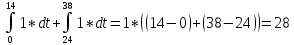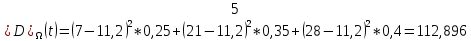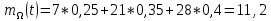Файл: Некоторое множество действительных чисел. Случайной функцией называется совокупность случайных величин.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 22
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теоретическая часть
Пусть T – некоторое множество действительных чисел. Случайной функцией называется совокупность случайных величин {X(t)}.
При наблюдении случайной функции мы получаем одну из возможных ее реализаций – неслучайную функцию. Поэтому случайную функцию можно рассматривать как совокупность всех ее возможных реализаций.
Если роль параметра t играет время, то случайную функцию называют случайным процессом. Если параметр дискретный, то соответствующие ему случайные величины образуют случайную последовательность.
Математическим ожиданием случайного процесса x(t) называют неслучайную функцию
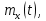 значение которой при каждом фиксированном значении параметра t равно математическому ожиданию сечения процесса при этом значении параметра, т.е.:
значение которой при каждом фиксированном значении параметра t равно математическому ожиданию сечения процесса при этом значении параметра, т.е.: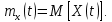
Дисперсией случайного процесса x(t) называют неслучайную функцию
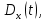 значение которой при каждом фиксированном значении параметра t равно дисперсии сечения процесса при этом значении параметра, т.е.:
значение которой при каждом фиксированном значении параметра t равно дисперсии сечения процесса при этом значении параметра, т.е.: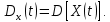
Формула расчёта математического ожидания:
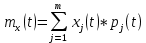 .
.Формула расчёта дисперсии:
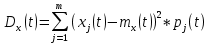 .
.Универсальной характеристикой любой случайной величины Х будь она непрерывной, дискретной или даже смешанной, является функция распределения F(x), которая определяет вероятность того, что случайная величина Х примет значение меньше любого заданного действительного числа х: F(x) = P(X < x). Эта функция и используется как характеристика случайного процесса X(t).
Если X – дискретная случайная величина, то закон распределения задается
рядом распределения:
| X | 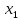 | 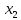 | … | 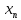 |
| P | 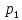 | 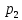 | … | 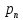 |
Постановка задания
Расчитать математическое ожидание и дисперсию случайных процессов для: 1) интенсивности поступления пассажиров; 2) потери времени ожидания транспортного обслуживания; 3) количества пассажиров, время ожидания которых превышает критическое.
Дано:
u(t)=
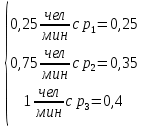
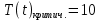
Найти:
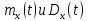 для каждого случая = ?
для каждого случая = ?Выполнение поставленных заданий
Формула расчёта математического ожидания:

Формула расчёта дисперсии:

1-й случай:
Для интенсивности поступления пассажиров.
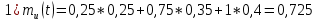
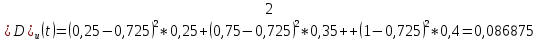
2-й случай:
Для потери времени ожидания транспортного обслуживания.
[Взята суммарная потеря
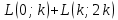 из первого расчётного задания]
из первого расчётного задания]
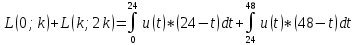
-
При u(t)=0,25
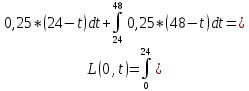
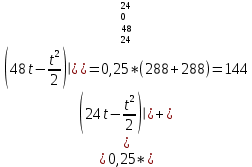
-
При u(t)=0,75
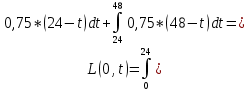
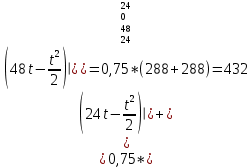
-
При u(t)=0,1
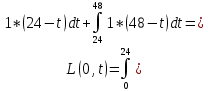
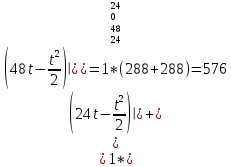
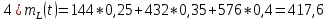
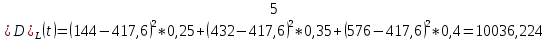
3-й случай:
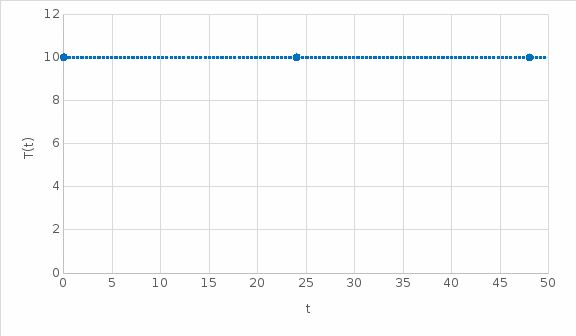
Для количества пассажиров, время ожидания которых превышает критическое
, где
 .
.
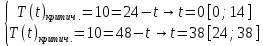

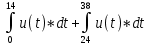
-
При u(t)=0,25
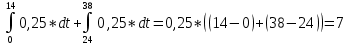
-
При u(t)=0,75
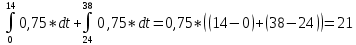
-
При u(t)=1