1. Постановка вариационных задач. Необходимые условия экстремума.

Вариационное исчисление является одним из основных методов современного естествознания. Свое начало берет от классического результата Я. Бурнулли (1696), решившего задачу о брахистохроне, так называемой кривой наискорейшего спуска.

Классическое вариационное исчисление посвящено анализу условий экстремума интегрального функционала

На некотором множестве G функций x(t), определенных и дифференцируемых на некотором множестве Ω С Rⁿ, со значениями на множестве R. Множество G определяется обычно дополнительными оговорками или условиями; множество Ω как правило связно и имеет связную внутренность.

Рассмотрим простейшую задачу классического вариационного исчисления:

Задача о брахистохроне:

Найти функцию x₀(t), минимизирующую функционал

на множестве функций x(t), принадлежащих классу гладкости C¹[a,b], удовлетворяющих

Необходимые условия

Условие Эйлера - Пуассона

Пусть задан функционал

Если функция x дает экстремум на G то она является решением уравнения Эйлера – Пуассона

дополненное краевыми условиями

--------------------------------------------------------------------------------

Условие Эйлера

Пусть задан функционал

Если функция x дает экстремум на G то она является решением уравнения Эйлера

Где

дополненное краевыми условиями

---

Условие ДюБуа – Раймонда

Пусть то интеграла

Где функция А достаточно регулярна и G={xЄC¹[a,b]: x(a)=A, x(b)=B}, тогда x_0(t) удовлетворяет уравнению Эйлера

Условие Лежандра:

На множестве G={xЄC¹[a,b]: x(a)=A, x(b)=B} задан функционал

Пусть , тогда Если же то

1. 1. При условиях ; исследовать на экстремум функционал

-----------------------------------------------------------------------------------------------

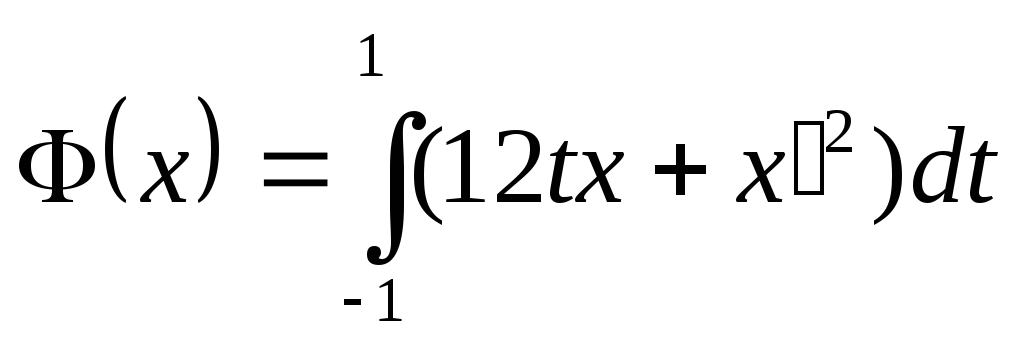
Пусть задан функционал

Если функция x дает экстремум на G то она является решением уравнения Эйлера

Где

дополненное краевыми условиями

-----------------------------------------------------------------------------------------------

Решение

Составим уравнение Эйлера:

Используем краевые условия:

---

Отсюда

Получаем

- допустимая экстремаль

1. 2.

Среди всех функций класса , удовлетворяющих граничным условиям ; , найти такую, которая реализует экстремум функционала

-----------------------------------------------------------------------------------------------

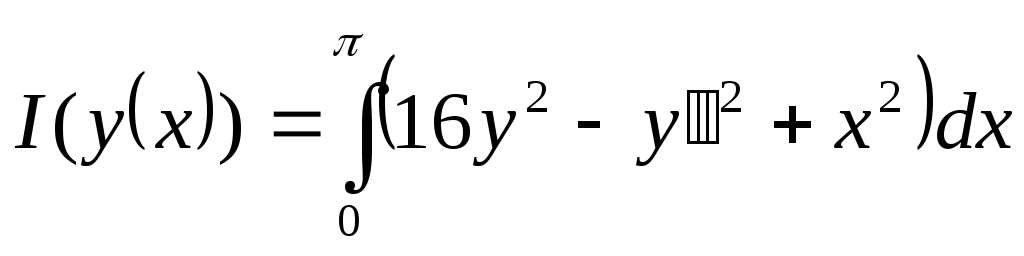
Пусть задан функционал

Если функция x дает экстремум на G то она является решением уравнения Эйлера – Пуассона

дополненное краевыми условиями

-----------------------------------------------------------------------------------------------

Решение

Используем уравнение Эйлера – Пуассона

32y-2y⁽⁴⁾=0

y⁽⁴⁾-16y=0

k⁴-16=0

k₁=2, k₂=-2, k₃=2i, k₄=-2i

y(x)=C₁e^2x+ C₂e^-2x+C₃cos2x+C₄sin2x

Подставим краевые условия

y(0)=C₁+ C₂+C₃=0

y(π)=C₁e^2π+ C₂e^-2π+C₃=0

y’(x)=2C₁e^2x-2C₂e^-2x-2C₃sin2x+2C₄cos2x

y’(0)=2C₁-2C₂+2C₄=1

y’(π)=2C₁e^2π-2C₂e^-2π+2C₄=1

Из этой системы найдем С₁, C₂, C₃, C₄.

С₁=0, C₂=0, C₃=1/2, C₄=0.

y(x)=1/2sin2x

1. 3.

При условиях ; ; ; . Найти экстремали функционала .

---

-----------------------------------------------------------------------------------------------

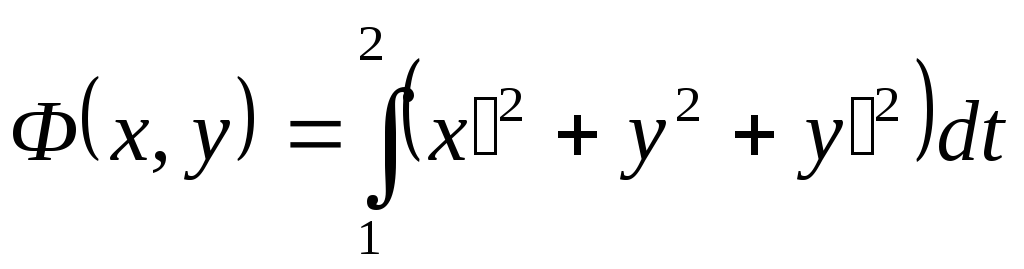Пусть задан функционал

Функция x дает экстремум на G если она является решением системы Эйлера

дополненное краевыми условиями

-----------------------------------------------------------------------------------------------

F_x=0, F_x’­=2x’

F_y=2y, F_y’=2y’

x=C₁t+C₂

y=C₃e^t+C₄e^-t

Используем краевые условия

C₁=1, C₂=0

C₃=1/(e²-1), C₄=e²/(1-e²)

2. Вариационные задачи на условный экстремум. Метод множителей Лагранжа.

Пусть в пространстве C¹[a,b] заданы функционалы

Ставится задача исследовать функционал Ф(x) на экстремум на множестве

G={x(t)Є C¹[a,b] | x(a)=A, x(b)=B, Ψ_i(x)=α_i , α_i=const}

Система решения поставленной задачи методом множителей Лагранжа:

1. Составим функцию Лагранжа

2. Выписываем уравнение Эйлера

3. Находим допустимые экстремали (решения уравнения Эйлера). Константы и значения λ_i определяем из условий

---

4. По определения min, max функционала исследуем знак разности

Где x₀ – допустимая экстремаль

Если , то

Если , то

2. 2.

При условиях, и связи исследовать на экстремум функционал .

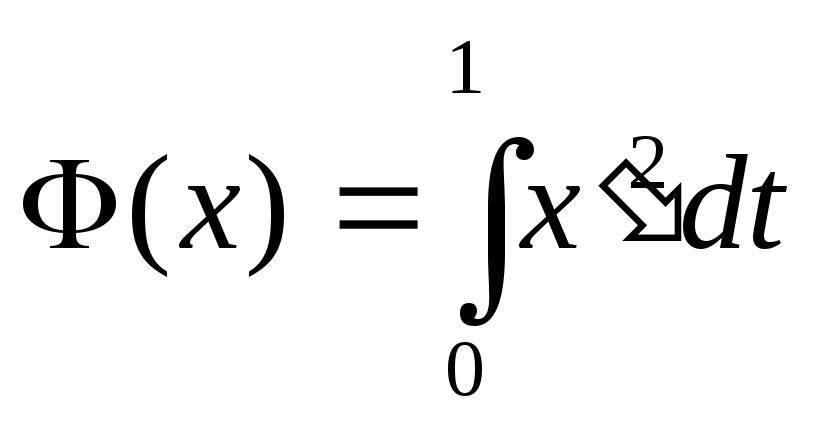1. Составим функцию Лагранжа

2. Выпишем уравнение Эйлера

3. 

Получаем - допустимая экстремаль

4. Пусть h=x-x₀

---

Смотрите также файлы

• БТВА (окончательная редакция) для печати.docx

• БП печи.doc

• Бизнес план.doc

• Арх.человек (фрагменты).doc

• Анализ русской народной сказки Морозко.docx