§ 34. Двойное векторное произведение

Пусть вектор а умножается векторно на вектор b, после чего получен­ный вектор [ab] умножается снова векторно на вектор с. В результате по­лучается так называемое двойное векторное произведение [[ab] с] (ясно, что [[ab] с] — вектор). Умножая вектор а векторно на [ab], получим двойное векторное произведение [a [[bс]].

Вообще говоря,

[[ab] с]  [a [bс]]

Докажем, что имеет место тождество

[[ab] с] = b(aс) — b(aс)

Доказательство. Введём (декартову прямоугольную) систему коор­динат. Чтобы облегчить выкладки, расположим оси координат специальным образом, а именно: ось Ох направим по вектору а, ось Оу поместим в плоскости векторов а и b (считая, что векторы а, b приведены к общему началу). В таком случае будем иметь:

a = {X₁; 0; 0}, b = {X₂; Y₂; 0}, с = {X₃; Y₃; Z₃},

Теперь находим:

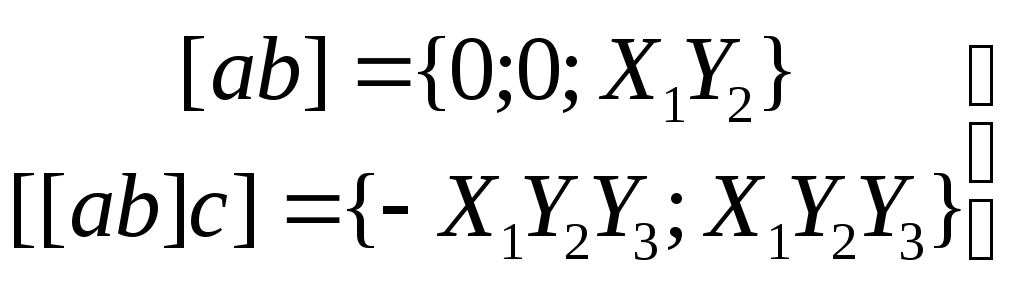
С другой стороны,

ас = Х₁Х₃; b(ас) = {Х₁Х₂Х,; Х₁X₂Х₃; 0},

bc = Х₂Х₃+ Y₂Y₃, a(bc) = {X₁X₂X₃ + X₁Y₂Y₃; 0; 0}.

Следовательно,

b (ас) — а (bс) = {— X₁X₂X₃; X₁Y₂Y₃; 0; }. (2)

Сравнивая правые части формул (1) и (2), получаем:

[[аb]с] = b(ас) — а(bс),

что и требовалось.

879. Доказать тождество

[a[bc]] = b(ac) — c(ab).

880. Решить задачу 864, используя тождества, данные в начале этого параграфа, и тождество задачи 879.

881. Даны вершины треугольника А(2; —1; —3), B(1; 2;—4) и С(3; —1; —2). Вычислить координаты вектора h, коллинеарного с его высотой, опущенной из вершины А на противоположную сторону, при условии, что вектор h образует с осью Оу тупой угол и что его модуль равен 2 .

---

882. Считая, что каждый из векторов а, b, с отличен от нуля, установить, при каком их взаимном расположении справедливо ра­венство

[a[bc]] = [[ab]c],

883. Доказать тождества:

1) [a[bc]] + [b] [ca] + [c[ab] = 0;

2) [ab] [cd] = (ас) (bd) — (ad) (bc);

3) [ab] [cd] + [ас] [db]+[ad] [bc] = 0;

4) [[ab] [cd]] = c(abd) — d(abc);

5) [ab] [bc] [ca] = (abc)²;

6) [а [а [а [ab]]]] = a⁴b при условии, что векторы а и b взаимно перпенди-кулярны;

7) [а (b [cd]]] = [ас] (bd) — [ad] (bc);

8) [a[b[cd]]] = (acd)b — (ab)[cd];

9) [аb]² [ас]² — ([ab] [ас]) = а² (аbс)²;

10) [[ab] [bc]} [[bс] [са]] [[са] [ab]] = (abc)⁴;

11) (аb) [cd] + (ас) \db] + (ad) [bc] = a (bcd);

12)

884. Три некомпланарных вектора a, b и с приведены к общему началу. Доказать, что плоскость, проходящая через концы этих векторов, перпендикулярна к вектору

[аb] + [bс] + [са

---

Смотрите также файлы

• kletenik_33.doc

• kletenik_32.doc

• kletenik_31.doc

• kletenik_30.doc

• kletenik_29.doc