ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.07.2024
Просмотров: 16
Скачиваний: 0
Лабораторная работа № 17
Выполнение регрессии и проведение аппроксимации. Функции сглаживания данных и предсказания.
Цель работы: Научиться выполнять обработку данных с помощью методов регрессии и аппроксимации, заложенных в MathCad.
Задание к работе:
К работе допущен:
Работу выполнил:
Работу защитил:
Теоретическая часть
Выполнение регрессии
Широко распространенной задачей обработки данных является представление их совокупности некоторой функцией y(x). Задача регрессии заключается в представлении параметров этой функции такими, чтобы функция приближала бы облако исходных точек (заданных векторами VX и VY) с наименьшей среднеквадратичной погрешностью.
Проведение линейной и сплайновой аппроксимаций
Для представления физических закономерностей и при проведении научно-технических расчетов часто используются зависимости вида y(x), причем число точек этих зависимостей ограничено. Неизбежно возникает задача приближенного вычисления значений функций в промежутках между узловыми точками (интерполяция) и за их пределами (экстраполяция). Эта задача решается аппроксимацией исходной зависимости, т. е. ее подменой какой-либо достаточно простой функцией. Система Mathcad представляет возможность аппроксимации двумя важными типами функций: кусочно-линейной и сплайновой.
-
Выполнение линейной регрессии
Чаще всего используется линейная регрессия, при которой функция y(x) имеет вид: y(x)=a+bx и описывает отрезок прямой.
Для проведения линейной регрессии в систему встроен ряд приведенных ниже функций:
corr(VX,VY) - возвращает скаляр - коэффициент корреляции Пирсона;
intercept(VX,VY) - возвращает значение параметра a (смещение линии регрессии по вертикали);
slope(VX,VY) - возвращает значение параметра b (угловой коэффициент линии регрессии).
Как видно из рисунка, прямая регрессия проходит в «облаке» исходных точек с максимальным среднеквадратичным приближением к ним. Чем ближе коэффициент корреляции к 1, тем точнее представленная исходными точками зависимость приближается к линейной.
-
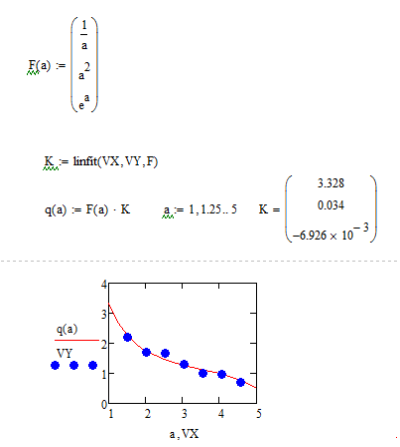
Реализация линейной регрессии общего вида
В MathCad 7 реализована возможность выполнения линейной регрессии общего вида. При ней заданная совокупность точек приближается функцией вида: F(x,K1,K1,...,KN)=K1*F1(x)+K2*F2(x)+...+KN*FN(x).
Таким образом, функция регрессии является линейной комбинацией функций F1(x),F2(x)...FN(x), причем сами эти функции могут быть нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции.
Для реализации линейной регрессии общего вида используется функция:
linfit(VX,VY,F) - возвращает вектор коэффициентов линейной регрессии К, при котором среднеквадратичная погрешность приближения «облака» исходных точек, координаты которых хранятся в векторах VX и VY, оказывается минимальной. Вектор должен содержать функции F1(x),F2(x)...FN(x), записанные в символьном виде.
3. Одномерная линейная аппроксимация
При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. Графически это означает просто соединение узловых точек отрезками прямых, для чего используется следующая функция:
linterp(VX,VY,x).
Для заданных векторов VX и VY узловых точек и заданного аргумента х linterp(VX,VY,x) возвращает значение функции при ее линейной аппроксимации. При экстраполяции используются отрезки прямых, проведенные через две крайние точки.
4. Одномерная сплайн-интерполяция
При небольшом количестве узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. При ней даже первая производная функции аппроксимации испытывает резкие скачки в узловых точках. Для целей экстраполяции функция linterp(VX,VY,x) не предназначена и за пределами области определения может вести себя непредсказуемо.
Гораздо лучшие результаты дает сплайн-аппроксимация. При ней исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закрепленную в узловых точках (откуда и название аппроксимации spline - гибкая линейка).
Для осуществления сплайновой аппроксимации система Mathcad предлагает четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн-функций при различном виде интерполяции:
cspline(VX,VY) - возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;
pspline(VX,VY) - возвращает вектор VS вторых производных при приближении в опорных точках к параболической кривой;
lspline(VX,VY) - возвращает вектор VS вторых производных при приближении к опорным точкам прямой.
Наконец, четвертая функция
nterp(VS,VX,VY,x) - возвращает значение y(x) для заданных векторов VS,VX,VY и заданного значения x.
5. Функции сглаживания данных
Данные большинства экспериментов имеют случайные составляющие погрешности. Поэтому часто возникает необходимость статистического сглаживания данных. Ряд функций MathCAD предназначен для выполнения операций сглаживания данных различными методами (рис. 72). Вот перечень этих функций:
medsmooth(VY,n)— для вектора с m действительными числами возвращает m-мерный вектор сглаженных данных по методу скользящей медианы, параметр n задает ширину окна сглаживания (n должно быть нечетным числом, меньшим m);
ksmooth(VX, VY, b) — возвращает n-мерный вектор сглаженных VY, вычисленных на основе распределения Гаусса. VX и VY — n-мерные векторы действительных чисел. Параметр b (полоса пропускания) задает ширину окна сглаживания ( b должно в несколько раз превышать интервал между точками по оси х );
supsmooth(VX, VY) — возвращает n-мерный вектор сглаженных VY, вычисленных на основе использования процедуры линейного сглаживания методом наименьших квадратов по правилу k-ближайших соседей с адаптивным выбором k. VX и VY — n-мерные векторы действительных чисел. Элементы вектора VX должны идти в порядке возрастания.
Функции предсказания данных.
Весьма интересной является функция предсказания predikt(data,k,N), где data — вектор данных, где data — вектор данных, k — число последних точек существующих данных, на основе которых происходит расчет предсказываемых точек; и N — число точек, в которых необходимо предсказать данные. Она по ряду заданных равномерно расположенных точек позволяет рассчитать некоторое число N последующих точек, т. е. по существу выполняет экстраполяцию произвольной (но достаточно гладкой и предсказуемой) зависимости.
Функция предсказания обеспечивает высокую точность при монотонных исходных функциях или функциях, представляемых полиномом невысокой степени
Практическая часть.
1.Введите матрицу координат точек на плоскости согласно № варианта.
2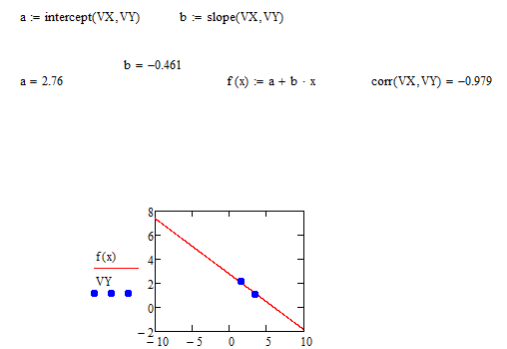
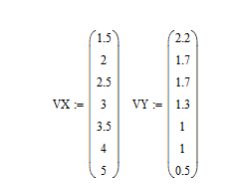.Постройте
функции линейной и обобщенной регрессии
для данных точек.
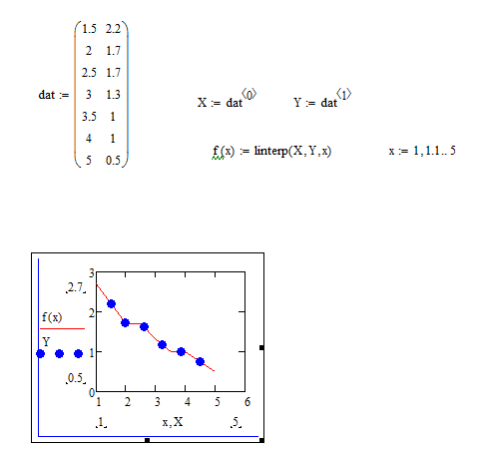
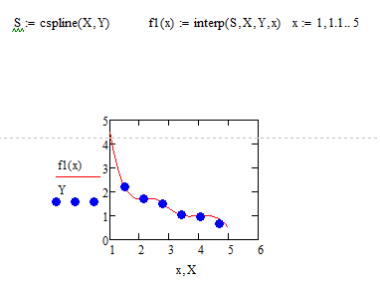
3.Постройте
линейную и сплайновую интерполяцию для
тех же точек
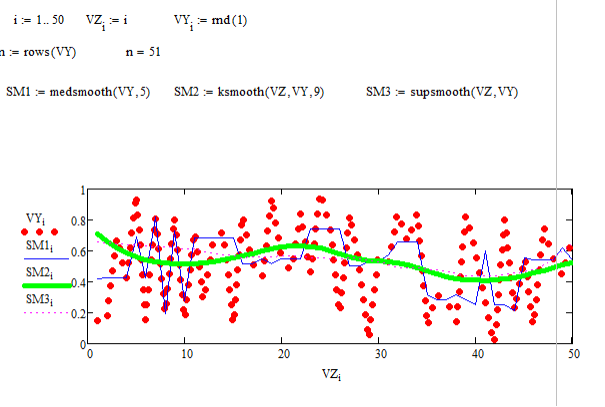4.С
помощью функции rnd введите 50 случайных
чисел из отрезка [0,2]. Постройте функции
сглаживания данных (с помощью различных
встроенных функций).
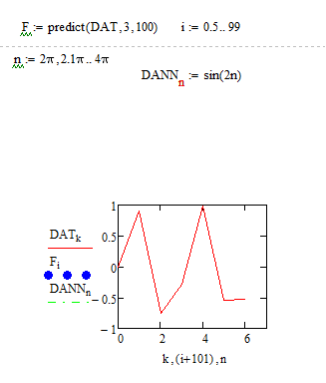
5.Предскажите поведение функции f(x) = sin(2x) на отрезке [2π, 4π], если предположить, что она задана на отрезке [0, 2π].
Заключение
Я Научился выполнять обработку данных с помощью методов регрессии и аппроксимации, заложенных в MathCad.