ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.07.2024
Просмотров: 109
Скачиваний: 0
СОДЕРЖАНИЕ
Цель работы
Построение эквипотенциальных поверхностей, создаваемых электродами различной формы и определение зависимости напряженности электрического поля от расстояния до его источника.
Введение
Вокруг заряда или заряженного тела возникает электрическое поле, которое характеризуется напряженностью Е и потенциалом φ. Напряженностью электрического поля в данной точке называется векторная величина, равная силе F, с которой электрическое поле действует на единичный положительный заряд q, помещенный в данную точку поля
Е = F/q . (I)
Напряженность является силовой характеристикой электрического поля. Единицей напряженности электрического поля в системе СИ является напряженность такого поля (или напряженность в такой точке поля), где на точечный заряд q = 1 Кл действует сила в 1Н. Единица напряженности не имеет собственного имени и названа по её размерности: 1 ед Е = 1Н/1Кл = 1 В/м.
Графически электрические поля изображаются линиями напряженности, которые начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Линиями напряженности называются кривые, касательные к которым совпадают с направлением вектора E. Густота линий напряженности нормируется по закону
dN/dS = E ,
где dN - число линий напряженности, пронизывающих перпендикулярную к ним площадку dS. Следовательно, густота нормированных линий напряженности характеризует численное значение вектора E.
Наряду с силовой характеристикой вводится энергетическая характеристика электрического поля, называемая потенциалом. Потенциал φ в данной точке электрического поля определяется отношением потенциальной энергии Wр точечного заряда q, помещенного в данную точку поля, к величине этого заряда
φ = Wр/q, (2)
За единицу потенциала в системе СИ принимается 1В (вольт). Один вольт - потенциал в такой точке поля, в которой электрический заряд в 1 кулон обладает потенциальной энергией в 1 джоуль: 1 В = 1Дж/1Кл.
Разность потенциалов двух точек электрического поля численно равна работе, которую надо совершить, чтобы переместить единичный заряд из одной точки поля в другую
φ2 – φ1 = А12/q
Если заряд q перемещается перпендикулярно силовым линиям, то работа при этом не совершается, и точки по траектории перемещения имеют равный потенциал. Геометрическое место точек с одинаковым потенциалом называется эквипотенциальной поверхностью. Линии напряженности всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности строятся таким образом, чтобы
φi+1 – φi = const,
т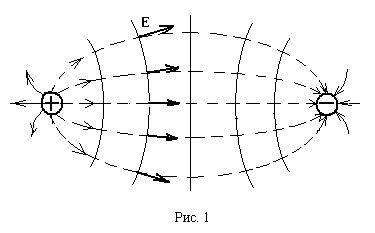 .
е. разность потенциалов между произвольно
взятыми соседними эквипотенциальными
поверхностями одинакова. На рисунке 1
дано графическое изображение электрического
поля, создаваемого разноименными
точечными зарядами. Эквипотенциальные
поверхности изображены сплошными
линиями, а линии напряженности –
пунктир-
.
е. разность потенциалов между произвольно
взятыми соседними эквипотенциальными
поверхностями одинакова. На рисунке 1
дано графическое изображение электрического
поля, создаваемого разноименными
точечными зарядами. Эквипотенциальные
поверхности изображены сплошными
линиями, а линии напряженности –
пунктир-
ными.
Между силовой и энергети- ческой характеристиками электрического поля для произвольного
направления l существует связь:
El = -dφ/dl. (3)
В векторном виде эта связь выражается соотношением
Е = - gradφ . (4)
Согласно (4) значение вектора напряженности электрического поля численно равно уменьшению потенциала вдоль силовой линии.
Если во внешнее электрическое поле поместить проводник, то свободные электроны в проводнике под действием силы F = - eE придут в движение в сторону, обратную направлению поля. В результате у концов проводника возникают заряды противоположного знака, называемые индуцированными зарядами. Поле этих зарядов направлено противоположно внешнему и, следовательно, накапливание зарядов у концов проводника приводит к ослаблению в нем поля. Движение электронов в проводнике происходит до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряженности вне проводника перпендикулярными к его поверхности (т. к. внешняя поверхность проводника является эквипотенциальной). Это справедливо и для полого проводника, который можно использовать в качестве экрана для электростатической защиты измерительных приборов от внешних полей. Здесь индуцированные заряды тоже распределяются по внешней поверхности проводника, следовательно, поле внутри полости отсутствует.
Т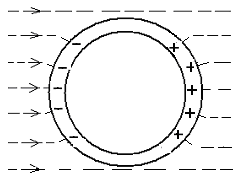 аким
образом, проводник, внесенный в
электрическое поле, разрывает часть
линий напряженности. Они заканчиваются
на отрицательных индуцированных зарядах
и вновь начинаются на положительных.
На рисунке 2 пунктирными линиями показаны
линии напряженности внешнего поля.
Явление возникновения на поверхности
проводника индуцированных зарядов
называется явлением
аким
образом, проводник, внесенный в
электрическое поле, разрывает часть
линий напряженности. Они заканчиваются
на отрицательных индуцированных зарядах
и вновь начинаются на положительных.
На рисунке 2 пунктирными линиями показаны
линии напряженности внешнего поля.
Явление возникновения на поверхности
проводника индуцированных зарядов
называется явлением
Рис. 2 электростатической индукции.
Описание установки
Электростатическое поле характеризуется в каждой точке пространства вектором напряженности Е и потенциалом φ. Учитывая связь между этими величинами (3), согласно которой линии напряженности и эквипотенциальные поверхности взаимно перпендикулярны, для исследования электростатического поля достаточно найти распределение в пространстве одной из этих двух характеристик поля. Так имея картину линий напряженности поля, можно построить систему эквипотенциальных поверхностей, и, наоборот, зная положение поверхностей равного потенциала, можно построить линии напряженности поля. Экспериментально проще изучать распределение потенциала, так как большинство приборов, пригодных для изучения полей, измеряют разности потенциалов, а не напряженности поля.
В основу изучения распределения потенциалов в электростатическом поле положен метод зондов. Сущность этого метода состоит во введении в исследуемую точку поля, создаваемого заряженными проводниками (электродами), специального электрода-зонда, соединенного с прибором, измеряющим приобретенный зондом потенциал относительно какой-либо точки поля, выбранной за начало отсчета потенциала. Для электростатических полей, создаваемых неподвижными зарядами в непроводящей среде, передача зонду потенциала той точки поля, в которую он помещен, сама по себе происходить не может. Для ее осуществления необходимо обеспечить стекание (или натекание) электрических зарядов с зонда, что в условиях непроводящей среды невозможно. В этом случае необходимо использовать такие зонды, которые создают местную ионизацию среды, например, плазменные зонды. Однако такое исследование осуществить довольно трудно.
На практике прямое излучение электростатического поля заменяют изучением его на более удобной модели, представляющей собой электрическое поле, создаваемое при прохождении низкочастотного тока в слабо проводящей среде между электродами, форма и взаимное расположение которых такие же, как и в изучаемом электростатическом поле. В этом случае, учитывая, что расстояние между электродами невелико, можно считать, что потенциалы во всех точках исследуемого поля изменяются синхронно и эквипотенциальные поверхности остаются неизменными.
Поскольку в однородной проводящей среде при прохождении по ней низкочастотного тока нет объемных электрических зарядов, поле в пространстве между электродами, к которым приложено напряжение, имеет ту же конфигурацию, какую оно имело бы в непроводящей среде или в вакууме, если электропроводимость проводящей среды много меньше электропроводимости электродов. Поэтому при исследовании электрического поля на описанной выше модели используются металлические электроды, а в качестве зонда - металлический стержень. В проводящей среде заряды будут натекать на зонд и он примет потенциал той точки поля, в которую помещен.
 Имея картину
распределения потенциала в изучаемом
поле, можно получить (провести) линии
напряженности поля, используя связь
между напряженностью и потенциалом
электростатического поля.
Имея картину
распределения потенциала в изучаемом
поле, можно получить (провести) линии
напряженности поля, используя связь
между напряженностью и потенциалом
электростатического поля.
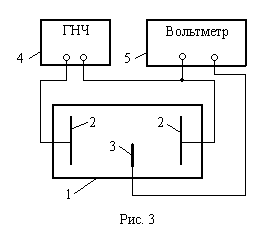
Лабораторная установка, изображенная на рис.3, представляет собой ванну 1, выполненную из материала с хорошими изоляционными свойствами. В ванну помещают металлические электроды 2, поле между которыми подлежит изучению, и наливают водопроводную воду слоем около 6мм.Проводимость такого слоя воды порядка 10-3-10-2 Ом-1м-1, а проводимость материала электродов 2 порядка107 Ом-1м-1.
На электроды подается переменное напряжение низкой частоты (50 Гц). Подаваемое напряжение от генератора низкой частоты (ГНЧ) 4 не должно превосходить 3В. В поле между электродами помещают зонд 3, соединенный с вольтметром переменного напряжения 5. Дно ванны имеет координатную сетку.
Помещая зонд в точки с определенными координатами, с помощью вольтметра 5 определяют потенциалы этих точек относительно одного из электродов.
Порядок выполнения измерений
1. Сетку, изображенную на дне ванны с водой, в уменьшенном масштабе перенести на бумагу.
2. Собрать электрическую схему установки. При этом электроды 1 должны быть расположены симметрично относительно оси координатной сетки. Включить приборы.
3. Зонд 3 поместить в точку, находящеюся на оси вблизи одного из электродов, записать показания вольтметра в разработанную таблицу и отметить на рисунке точку с найденным значением потенциала.
4. Смещая зонд с координатной оси, найти координату другой точки, имеющей то же значение потенциала (с точностью до 0,02 В). Найти координаты еще 4 точек, имеющих такой же потенциал и расположенных по ту же сторону координатной оси, а затем найти аналогичные точки с другой стороны этой координатной оси. Отметить на рисунке найденные точки.
5. Повторить измерения для других значений потенциала, получив
не менее 7 линий равного потенциала.
6. Аналогичные измерения провести для электродов другой конфигура-
ции, указанных преподавателем.
Обработка результатов измерений
1. Зарисовать картины полученных эквипотенциальных поверхностей.
2. Провести на рисунках не менее 5 силовых линий электрического поля.
3.
Построить график зависимости потенциала
поля φ
от
расстояния
r![]() между
электродами для точек, принадлежащих
координатной оси,
соединяющей центры электродов. Начало
отсчета координат φ
= φ(r)
совместить
с поверхностью электрода, вблизи которого
зарегистрирован
наименьший потенциал.
между
электродами для точек, принадлежащих
координатной оси,
соединяющей центры электродов. Начало
отсчета координат φ
= φ(r)
совместить
с поверхностью электрода, вблизи которого
зарегистрирован
наименьший потенциал.
4. Пользуясь построенным графиком, методом численного дифференцирования найти напряженность Е поля для разных значений r, основываясь на уравнении (3) в конечных величинах:
Е
= -
![]() ,
(5)
,
(5)
где
Δφ - изменение потенциала на отрезке Δr
= 10мм. Расчет по формуле (5) производить
следующим образом. Выбрав значение r1,
установить по графику соответствующее
значение
![]() ,
а затем значение
,
а затем значение
![]() дляr2
= r1
+
Δr.
Разделив Δφ = φ2
–
φ1
на Δr,
получим числовое значение напряженности
Е поля, которое следует отнести к середине
выбранного интервала Δr.
Расчет выполнить для значений r,
охватывающих весь интервал расстояний
между электродами. Результаты расчетов
занести в таблицу.
дляr2
= r1
+
Δr.
Разделив Δφ = φ2
–
φ1
на Δr,
получим числовое значение напряженности
Е поля, которое следует отнести к середине
выбранного интервала Δr.
Расчет выполнить для значений r,
охватывающих весь интервал расстояний
между электродами. Результаты расчетов
занести в таблицу.
5. Построить график зависимости напряженности Е электрического поля от расстояния r между электродами вдоль оси координатной сетки.
Контрольные вопросы
Что называется напряженностью, потенциалом электрического поля?
Какая связь существует между силовой и энергетической характеристиками поля?
Как графически изображаются электрические поля?
Какие линии называются линиями напряженности электрического поля?
Дать понятие эквипотенциальных поверхностей.
В чем заключается явление электростатической индукции?
Объясните возможность использования полых проводников в качестве экранов от внешних полей.