Файл: Курсовая работа. Исследование релейной следящей системы.docx

Исследование следящей системы, содержащей датчик угла рассогласования, релейный усилитель напряжений, электромеханический усилитель мощности, исполнительный двигатель иредуктор.

Функциональная схемасистемы:

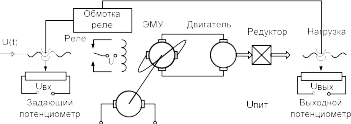
Задание

Составить структурную схемуСАР.
Произвести исследование САР методом фазовойплоскости:

аппроксимировать линейную часть звеном с передаточной функцией графически ианалитически;

_kes

^s^Ts^¹

построить фазовый портрет системы и определить амплитуду и частоту автоколебаний; построить фазовые траектории свободного движения при заданных начальных
условиях: Х1 = 3b , Х2 =0;
построить соответствующие переходныепроцессы;
произвести расчет автоколебаний графически ианалитически.

Произвести исследование САР методом гармоническойлинеаризации:

найти коэффициенты гармонической линеаризации нелинейного звена и составить выражение его эквивалентного комплексного коэффициентапередачи;
найти частотным методом (с помощью АФЧХ и с помощью ЛАХ) амплитуду и частоту предельногоцикла;

произвести анализ устойчивости предельных циклов и найти параметрыавтоколебаний;

Произвести анализ вынужденного движения системы.

Произвести сравнительный анализ результатов исследования САР указанными методами.

Исходное данные

Вариант 1

U_cp,B

^Uном.дв.^,^B

T_э,c

T_дв,c

К_д,^вмм

K_э

_К_дв_,_рад

сВ

_К_р_,_мм

рад

0.005

110

0.05

0.20

0.03

Значение коэффициента возврата: m=-1

Начальные условия: : Х1 = 3b , Х2 = 0;

Структурная схема САР

Составим структурную схему системы автоматического регулирования по имеющейсяфункциональной.

Выражения для передаточных функций отдельных элементов САР.

Датчик:

W_дK_д

Реле:

Реле представляет собой нелинейный элемент, и его характеристика задается графически.

ЭМУ:

^T_э^U^&₂_^t^^^U₂_^t^^^K_э^U₁_^t^

Электродвигатель:

W_э_s__

К_э

T_эs1

^T_д_в^^&^^t^^^^&^^t^^^K_д_в^U₂_^t^

Редуктор

W_pК_р

W_э_s__

^Кдв

^s^^T_дв^s^¹

Нелинейный элемент

Параметры нелинейного элемента можно рассчитать по схеме.

b_p= U_cp= 0,005 В;

т*b_р=- b_р=0,005 В;

Напряжение на входе двигателя - это напряжение на выходе реле, усиленное с помощью ЭМУ.

Таким образом, можно записать:U_де=с_р•К_э.Отсюда найдем с_р.

Входное напряжение двигателяU_дв=110 В. Коэффициент усиления ЭМУ К_э=24 .

Напряжение на выходе релеc_p

_^Uдв

К_э

Нелинейный элемент приводится к обобщенному виду с учетом коэффициентов усиления в структурной схеме. Для этого пересчитываем его коэффициенты.

b^b^p

K_д

= 0,167

cc_pK_эK_двK_р= 36,3

Исследуемая система третьего порядка. Для построения фазового портрета необходимо понизить порядок на единицу.

Аппроксимация линейной части

Как и говорилось выше, после всех структурных преобразований мы получили систему третьего порядка. Понизить порядок можно, аппроксимировав колебательное звено последовательным соединением апериодического звена и звена «чистое запаздывание». Таким образом, вместо системы, описываемой передаточной функцией вида:

W_л