Файл: Методы численного решения дифференциальных уравнений первого порядка.doc

Методы численного решения дифференциальных уравнений первого порядка

Дифференциальным уравнением первого порядка называют уравнение вида:

. (1)

При численном решении дифференциального уравнения первого порядка вида (1) с начальным условием Y(x₀) = y₀ (задача Коши) сначала выбираем фиксированное приращение аргумента h = (x_n -x₀ )/n, где x_n - конечная точка интервала интегрирования, n - число шагов. Далее, используя один из итерационных методов численного интегрирования дифференциальных уравнений первого порядка, находим значение Y(x_n).

Метод Эйлера

Метод Эйлера относится к наиболее простым, базовым методам решения дифференциальных уравнений. Этот метод основан на представлении производной в конечно-разностной форме:

(2)

Так, для дифференциального уравнения вида (1) при достаточно малых значениях приращения аргумента x, можно, представив производную в виде отношения приращения функции к приращению аргумента, получить следующее приближенное представление в виде конечно-разностного уравнения:

(3)

Из этого представления легко выразить «новое» значение функции (значение функции в точке x+h) – расчетную формулу метода Эйлера:

(4)

Описание алгоритма численного интегрирования дифференциального уравнения первого порядка методом Эйлера:

1. Задаем начальное x₀ и конечное x_n значения отрезка интегрирования, начальное y0, т.е. значение функции y в точке x₀, а также количество шагов интегрирования n.

2. Вычисляем величину шага интегрирования h.

3. Задаем цикл по k от 2 до n+1.

4. В цикле на основе значения x_k-1 вычисляем x_k, т.е. x₁ = x₀+ h, x₂ = x₁+ h и т.д.

5. В цикле на основе значения Y_k-1 по рекуррентной формуле вычисляем y_k, т.е. Y₁=Y₀+h*F(x₀,Y₀), Y₂=Y₁+h*F(x₁,Y₁) и т.д. Значение F(x_k,Y_k) должно вычисляться в функции, соответствующей правой части дифференциального уравнения. Конец цикла.

6. Конец алгоритма.

Алгоритм численного интегрирования дифференциального уравнения первого порядка методом Эйлера на естественном языке:

x0=начальное_значение_х

xn=конечное_значение_х

y0=начальное_значение_Y

n=количество_шагов_интегрирования

h=(xn-x0)/n

ОПРЕДЕЛИТЬ МАССИВ X(n+1)

ОПРЕДЕЛИТЬ МАССИВ Y(n+1)

X(1)=x0

Y(1)=y0

Цикл по i от 2 до n+1

X(i)=X(i-1)+h

Y(i)=Y(i-1)+h*F(X(i-1),Y(i-1))

Конец цикла

Печать " Решение: Значения х Значения Y(х) :"

Цикл по i от 1 до n+1

Печать X(i),Y(i)

Конец цикла

ОПРЕДЕЛИТЬ ФУНКЦИЮ F

ПАРАМЕТРЫ x,y

f=.... *** Задается вид функции

ВЕРНУТЬ f

КОНЕЦ ОПРЕДЕЛЕНИЯ ФУНКЦИИ

Покажем пример реализации метода Эйлера на примере уравнения

, т.е. (5)

При аналитическом интегрировании данного уравнения получаем начальное значение функции в точке x₀=0 и вид искомой функции:

, .

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка методом Эйлера на VFP для уравнения (5):

SET DECIMALS TO 8

CLEAR

* Начальное и конечное значения х

x0=0

xn=1

* Начальное значение y

y0=1

* Количество итераций

n=10

h=(xn-x0)/n

DIMENSION X(n+1),Y(n+1)

X(1)=x0

Y(1)=y0

*Y(i+1)=Y(i)+h*F(X(i),Y(i))

FOR i=2 TO n+1

X(i)=X(i-1)+h

Y(i)=Y(i-1)+h*F(X(i-1),Y(i-1))

ENDFOR

? " Решение :”

? " Значения Х Известные значения Y Вычисленные значения Y :"

FOR i=1 TO n+1

?X(i),F_test(X(i)),Y(i)

ENDFOR

function F

lPARAMETERS x,y

f=y

RETURN f

ENDFUNC

function F_test

lPARAMETERS x

F_test=EXP(x)

RETURN F_test

ENDFUNC

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка методом Эйлера на VBA для уравнения (5):

Sub Euler_Test()

' Начальное и конечное значения х

x0 = 0

xn = 1

' Начальное значение y

y0 = 1

' Количество итераций

n = 10

h = (xn - x0) / n

ReDim x(n + 1)

ReDim y(n + 1)

x(1) = x0

y(1) = y0

'Y(i+1)=Y(i)+h*F(X(i),Y(i))

For i = 2 To n + 1

x(i) = x(i - 1) + h

y(i) = y(i - 1) + h * F(x(i - 1), y(i - 1))

Next i

Debug.Print "РЕШЕНИЕ :"

Debug.Print "Х Y Y test DaltaY"

For i = 1 To n + 1

delta = Abs(y(i) - Y_test(x(i)))

Debug.Print Format(x(i), "0.000"), _

Format(y(i), "0.000 000"), _

Format(Y_test(x(i)), "0.000 000"), _

Format(delta, "0.000 000")

Next i

End Sub

Function F(x, y)

F = y

End Function

Function Y_test(x)

Y_test = Exp(x)

End Function

Результат работы программы:

РЕШЕНИЕ :

Х Y Y test DaltaY

0,000 1,000 000 1,000 000 0,000 000

0,100 1,100 000 1,105 171 0,005 171

0,200 1,210 000 1,221 403 0,011 403

0,300 1,331 000 1,349 859 0,018 859

0,400 1,464 100 1,491 825 0,027 725

0,500 1,610 510 1,648 721 0,038 211

0,600 1,771 561 1,822 119 0,050 558

0,700 1,948 717 2,013 753 0,065 036

0,800 2,143 589 2,225 541 0,081 952

0,900 2,357 948 2,459 603 0,101 655

1,000 2,593 742 2,718 282 0,124 539

Для данного уравнения решение дифференциального уравнения первого порядка с шагом 0,1 дает точность порядка 0,1 (на последнем шаге). При решении с шагом 0,01 точность возрастает до порядка 0,01 (на последнем шаге).

Метод Кранка-Николсона

Метод Кранка-Николсона представляет собой модификацию метода Эйлера, в которой правая часть разностной формы дифференциального уравнения представляется в виде среднего значения правой части в точке x и правой части в точке x+h:

(6)

Поскольку искомое значение функции в точке x+h присутствует и в левой и в правой части уравнения – эта формула содержит Y(x+h) неявно, поэтому, для получения расчетной формулы необходимо выразить Y(x+h) явно. Выразить явно Y(x+h) возможно не для любого вида F(Y(x),x). Если правая часть дифференциального уравнения зависит только от x – F(x), тогда метод Кранка-Николсона можно применять для любого вида F(x).

Рассмотрим пример дифференциального уравнения с разрешимой правой частью, зависящей от x и Y(x):

, (7)

Запишем разностный вид этого дифференциального уравнения:

После простых преобразований:

1) ,

2) ,

3) .

Получим расчетную формулу:

. (8)

В случае, когда правая часть дифференциального уравнения зависит только от х, рекуррентная формула метода Кранка-Николсона имеет вид:

(9)

Например, для дифференциального уравнения с правой частью, зависящей только от x:

(10)

формула Кранка-Николсона имеет вид:

. (11)

Описание алгоритма численного интегрирования дифференциального уравнения первого порядка с правой частью уравнения, зависящей только от х, методом Кранка-Николсона:

7. Задаем начальное x₀ и конечное x_n значения отрезка интегрирования, начальное y0, т.е. значение функции y в точке x₀, а также количество шагов интегрирования n.

8. Вычисляем величину шага интегрирования h.

9. Задаем цикл по k от 2 до n+1.

10. В цикле на основе значения x_k-1 вычисляем x_k, т.е. x₁ = x₀+ h, x₂ = x₁+ h и т.д.

11. В цикле на основе значения Y_k-1 по рекуррентной формуле вычисляем y_k, т.е. Y₁=Y₀+h*(F(x₀,Y₀)+F(x₁,Y₁))/2, Y₂=Y₁+h*(F(x₁,Y₁)+F(x₂,Y₂))/2 и т.д. Значение F(x_k,Y_k) должно вычисляться в функции, соответствующей правой части дифференциального уравнения. Конец цикла.

12. Конец алгоритма.

Алгоритм численного интегрирования дифференциального уравнения первого порядка с правой частью уравнения, зависящей только от х, методом Кранка-Николсона на естественном языке:

x0=начальное_значение_х

xn=конечное_значение_х

y0=начальное_значение_Y

n=количество_шагов_интегрирования

h=(xn-x0)/n

ОПРЕДЕЛИТЬ МАССИВ X(n+1)

ОПРЕДЕЛИТЬ МАССИВ Y(n+1)

X(1)=x0

Y(1)=y0

Цикл по i от 2 до n+1

X(i)=X(i-1)+h

Y(i)=Y(i-1)+h*(F(X(i-1),Y(i-1))+ F(X(i),Y(i)))/2

Конец цикла

Печать " Решение: Значения х Значения Y(х) :"

Цикл по i от 1 до n+1

Печать X(i),Y(i)

Конец цикла

ОПРЕДЕЛИТЬ ФУНКЦИЮ F

ПАРАМЕТРЫ x,y

f=.... *** Задается вид функции

ВЕРНУТЬ f

КОНЕЦ ОПРЕДЕЛЕНИЯ ФУНКЦИИ

Покажем пример реализации метода Кранка-Николсона на примере уравнения (10). При аналитическом интегрировании уравнения (10) получаем начальное значение функции в точке x₀=0 и вид искомой функции:

, . (12)

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка с правой частью, зависящей только от х, методом Кранка-Николсона на VFP для уравнения (10):

SET DECIMALS TO 8

CLEAR

* Начальное и конечное значения х

x0=0

xn=1

* Начальное значение y

y0=3

* Количество итераций

n=10

h=(xn-x0)/n

DIMENSION X(n+1),Y(n+1)

X(1)=x0

Y(1)=y0

*Y(i+1)=Y(i)+h*F(X(i),Y(i))

FOR i=2 TO n+1

X(i)=X(i-1)+h

Y(i)=Y(i-1)+h*F(X(i-1),Y(i-1))

ENDFOR

? " Решение :"

? " Значения Х Известные значения Y Вычисленные значения Y :"

FOR i=1 TO n+1

?X(i),F_test(X(i)),Y(i)

ENDFOR

function F

lPARAMETERS x,y

f=x*x+3*x

RETURN f

ENDFUNC

function F_test

lPARAMETERS x

F_test=2*x+3

RETURN F_test

ENDFUNC

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка с правой частью, зависящей только от х, методом Кранка-Николсона на VBA для уравнения (10):

Sub Krank_Nikolson_Test()

' Начальное и конечное значения х

x0 = 0

xn = 1

' Начальное значение y

y0 = 3

' Количество итераций

n = 10

h = (xn - x0) / n

ReDim x(n + 1)

ReDim Y(n + 1)

x(1) = x0

Y(1) = y0

'Y(x+h) = Y(x) + h*(x^2 + 3*x + (x+h)^2 + 3*(x+h))/2

For i = 2 To n + 1

x(i) = x(i - 1) + h

Y(i) = Y(i - 1) + h * (f(x(i - 1), Y(i - 1)) + f(x(i), Y(i))) / 2

Next i

Debug.Print "РЕШЕНИЕ :"

Debug.Print "Х Y Y test DaltaY"

For i = 1 To n + 1

delta = Abs(Y(i) - Y_test(x(i)))

Debug.Print Format(x(i), "0.000"), _

Format(Y(i), "0.000 000"), _

Format(Y_test(x(i)), "0.000 000"), _

Format(delta, "0.000 000")

Next i

End Sub

Function f(x, Y)

f = x ^ 2 + 3 * x

End Function

Function Y_test(x)

Y_test = (x ^ 3) / 3 + 3 / 2 * (x ^ 2) + 3

End Function

Результат работы программы:

РЕШЕНИЕ :

Х Y Y test DaltaY

0,000 3,000 000 3,000 000 0,000 000

0,100 3,015 500 3,015 333 0,000 167

0,200 3,063 000 3,062 667 0,000 333

0,300 3,144 500 3,144 000 0,000 500

0,400 3,262 000 3,261 333 0,000 667

0,500 3,417 500 3,416 667 0,000 833

0,600 3,613 000 3,612 000 0,001 000

0,700 3,850 500 3,849 333 0,001 167

0,800 4,132 000 4,130 667 0,001 333

0,900 4,459 500 4,458 000 0,001 500

1,000 4,835 000 4,833 333 0,001 667

Как видно из приведенного примера, решение дифференциального уравнения первого (10) порядка с шагом 0,1 дает точность порядка 0,001 (на последнем шаге). При интегрировании с шагом 0,01 точность вычислений возрастает до 0,00001 (на последнем шаге).

Таким образом, сравнивая методы Эйлера и Кранка-Никольсона можно отметить следующее: метод Кранка-Никольсона как минимум в 100 раз точнее метода Эйлера, при этом точность вычислений существенно возрастает при уменьшении шага интегрирования.

Однако, метод Кранка-Никольсона удобно применять в тех случаях, когда правая часть дифференциального уравнения зависит только от х. Существуют также методы интегрирования, учитывающие зависимость правой части уравнения и от х и от Y(x), например, методы Рунге-Кутты.

Метод Рунге-Кутты четвертого порядка для решения уравнения первого порядка

Наиболее употребительным методом Рунге-Кутты решения уравнения первого порядка вида (1) является метод четвертого порядка, в котором вычисления производятся по формуле:

, (13)

где:

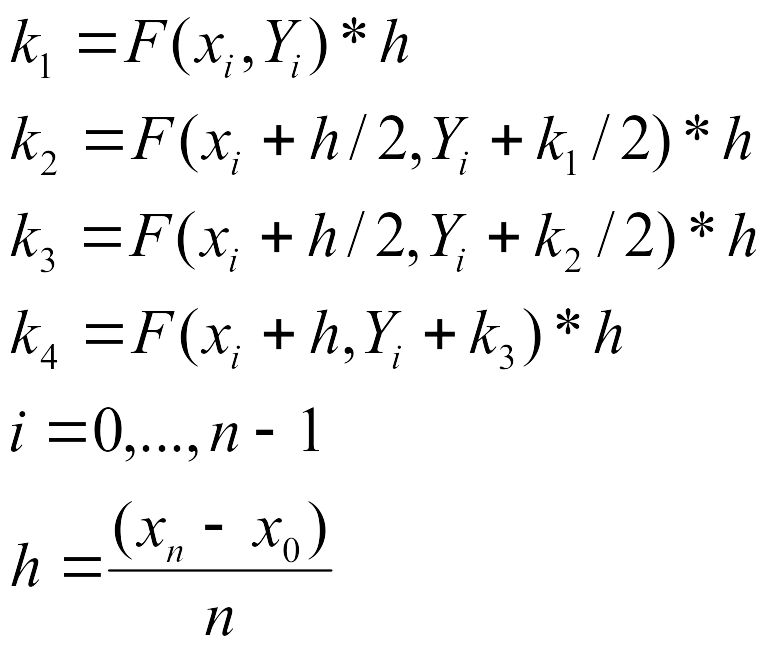(14)

Описание алгоритма метода Рунге-Кутты решения уравнения первого порядка:

1. Задаем начальное x₀ и конечное x_n значения отрезка интегрирования, начальное y0, т.е. значение функции y в точке x₀, а также количество шагов интегрирования n.

2. Вычисляем величину шага интегрирования h.

3. Цикл по х от х₀ до х_n с шагом h .

4. Вычисляем k1 = F(x , y )*h.

5. Вычисляем x1 = x +h/2.

6. Вычисляем Y1 = Y +K1 /2.

7. Вычисляем k2 = F(x1,y1)*h.

8. Вычисляем k2 = F(x1,y1)*h.

9. Вычисляем Y2 = Y+K2 /2.

10. Вычисляем k3 = F(x1,y2)*h.

11. Вычисляем x4 = x+h.

12. Вычисляем y4 = Y+K3.

13. Вычисляем k4 = F(x4,y4)*h.

14. Вычисляем Y = Y +(k1 +2*k2 +2*k3 +k4 )/6.

15. Конец цикла.

13. Определить функцию F(x,y).

14. Задать вид функции F(x,y).

15. Конец функции.

Алгоритм метода Рунге-Кутты 4-го порядка для решения дифференциального уравнения первого порядка на естественном языке:

х₀ = значение_левой_границы

х_n = значение_правой_границы

Y = начальное_значение_функции

n=количество_шагов_интегрирования

h = (x_n-x₀)/n

Цикл по x от x₀ до x_n с шагом h

k1 = F(x , y )*h

x1 = x +h/2

Y1 = Y +K1 /2

k2 = F(x1,y1)*h

Y2 = Y+K2 /2

k3 = F(x1,y2)*h

x4 = x+h

y4 = Y+K3

k4 = F(x4,y4)*h

Y = Y +(k1 +2*k2 +2*k3 +k4 )/6

КонецЦикла

ОПРЕДЕЛЕНИЕ ФУНКЦИИ F

ПАРАМЕТРЫ x,y

F=… *** задается вид функции

КонецФункции

Приведем примеры реализаций метода Рунге-Кутта для ранее рассмотренного уравнения (см. метод Эйлера) и сравним точность вычислений методом Эйлера и Рунге-Кутта.

Пример реализация алгоритма численного интегрирования дифференциального уравнения первого порядка на VFP для уравнения (5):

CLEAR

x0 = 0

xn = 1

y = 1

n = 10

h = (xn-x0)/n

?" X Тестовые Y_test Вычисленные Y Delta(Y_test-Y)"

for x=x0 to xn step h

k1 = F(x , y )*h

x1 = x +h/2

Y1 = Y +K1 /2

k2 = F(x1,y1)*h

Y2 = Y+K2 /2

k3 = F(x1,y2)*h

x4 = x+h

y4 = Y+K3

k4 = F(x4,y4)*h

Y = Y +(k1 +2*k2 +2*k3 +k4 )/6

delta=ABS(Y_test(x)-Y)

? x,Y_test(x),Y,delta

ENDFOR

Function F(x, y)

F=y

RETURN F

EndFunc

Function Y_test(x)

Y_test=EXP(x)

RETURN Y_test

EndFunc

Пример реализации алгоритма численного интегрирования дифференциального уравнения первого порядка методом Рунге-Кутта на VBA для уравнения (5):

Sub Test_Runge_Kytt()

Dim x(), y()

x0 = 0: xn = 1

y0 = 1

n = 100

ReDim y(n + 1): ReDim x(n + 1)

Call runge(0, 1, y0, x(), y(), n)

For i = 1 To n

ActiveSheet.Cells(i, 1).Value = x(i)

ActiveSheet.Cells(i, 2).Value = y(i)

y_test = f_test(x(i))

delta_y = Abs(y_test - y(i))

Debug.Print "x= " & Format(x(i), "0.000") & " : y= " & Format(y(i), "0.000 000 000 000") & " : y_test= " _

& Format(y_test, "0.000 000 000 000") & " : delta_y= " & Format(delta_y, "0.000 000 000 000")

Next i

Call AddChart(1, 2)

End Sub

Sub runge(x0, xn, y0, x(), y(), n)

Dim i, h, dk

h = (xn - x0) / n

k1 = h * f(x0, y0)

k2 = h * f(x0 + h / 2, y0 + k1 / 2)

k3 = h * f(x0 + h / 2, y0 + k2 / 2)

k4 = h * f(x0 + h, y0 + k3)

dk = 1 / 6 * (k1 + 2 * k2 + 2 * k3 + k4)

y(1) = y0 + dk

x(1) = x0 + h

For i = 1 To n

k1 = h * f(x(i), y(i))

k2 = h * f(x(i) + h / 2, y(i) + k1 / 2)

k3 = h * f(x(i) + h / 2, y(i) + k2 / 2)

k4 = h * f(x(i) + h, y(i) + k3)

dk = 1 / 6 * (k1 + 2 * k2 + 2 * k3 + k4)

y(i + 1) = y(i) + dk

x(i + 1) = x(i) + h

Next i

End Sub

Function f(x, y)

f = y

End Function

Function f_test(x)

f_test = Exp(x)

End Function

Sub AddChart(Col1, Col2)

ASheetName = Application.ActiveSheet.Name

Charts.Add

ActiveChart.ChartType = xlLine

ActiveChart.SetSourceData Source:=Sheets(ASheetName).Range("A1:B100"), PlotBy _

:=xlColumns

ActiveChart.SeriesCollection(1).Delete

ActiveChart.SeriesCollection(1).XValues = "=" & ASheetName & "!C1"

ActiveChart.Location Where:=xlLocationAsObject, Name:=ASheetName

With ActiveChart

.HasTitle = False

.Axes(xlCategory, xlPrimary).HasTitle = False

.Axes(xlValue, xlPrimary).HasTitle = False

End With

End Sub

В данной реализации все значения вычисляемой функции и ее аргумента хранятся в массивах, также использована процедура AddChart MS EXCEL для построения графика значений вычисляемой функции.

Результаты работы программы на VBA:

x=0,10:y=1,105 170 833 333:y_test=1,105 170 918 076:delta_y=0,000 000 084 742

x=0,20:y=1,221 402 570 851:y_test=1,221 402 758 160:delta_y=0,000 000 187 309

x=0,30:y=1,349 858 497 063:y_test=1,349 858 807 576:delta_y=0,000 000 310 513

x=0,40:y=1,491 824 240 081:y_test=1,491 824 697 641:delta_y=0,000 000 457 561

x=0,50:y=1,648 720 638 597:y_test=1,648 721 270 700:delta_y=0,000 000 632 103

x=0,60:y=1,822 117 962 092:y_test=1,822 118 800 391:delta_y=0,000 000 838 299

x=0,70:y=2,013 751 626 597:y_test=2,013 752 707 470:delta_y=0,000 001 080 874

x=0,80:y=2,225 539 563 292:y_test=2,225 540 928 492:delta_y=0,000 001 365 200

x=0,90:y=2,459 601 413 780:y_test=2,459 603 111 157:delta_y=0,000 001 697 377

x=1,00:y=2,718 279 744 135:y_test=2,718 281 828 459:delta_y=0,000 002 084 324

Как видно из результатов программы, метод Рунге-Кутты 4-го при шаге интегрирования 0,1 дает точность порядка 0,00001. При интегрировании с шагом 0,01 данный метод дает точность порядка 10^-9.

Сравнивая результаты работы трех приведенных методов решения дифференциальных уравнений первого порядка, приходим к выводу, что метод Рунге-Кутты является гораздо более точным, чем методы Эйлера и Кранка-Никольсона.

Методы численного решения систем дифференциальных уравнений

Гармонические колебания

Уравнение, описывающее идеальный периодический процесс (гармонические колебания), представляет собой дифференциальное уравнение второго порядка:

(15)

Это уравнение легко можно записать в виде системы дифференциальных уравнений первого порядка:

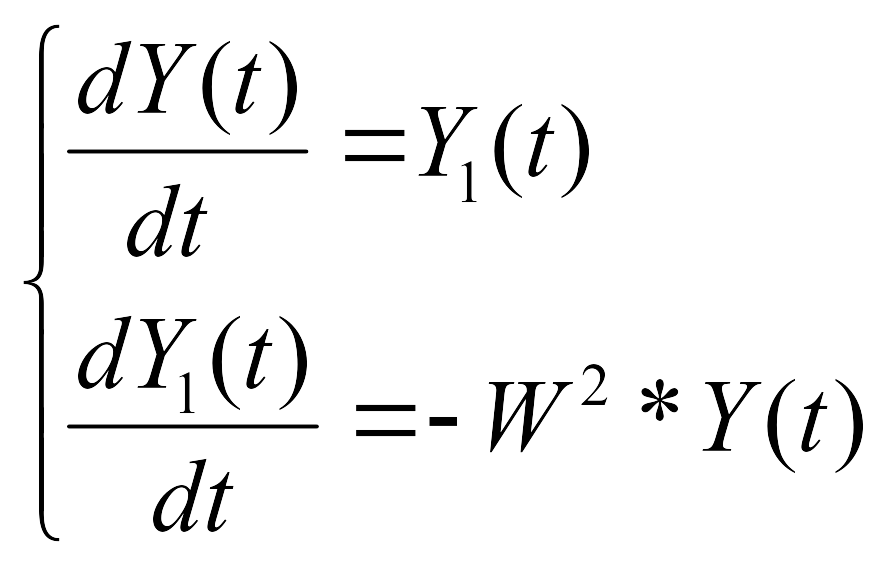(16)

Эту систему можно записать в матричном виде:

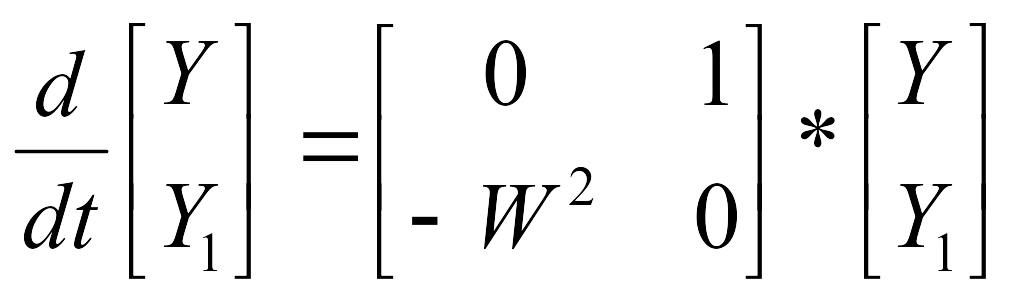, или 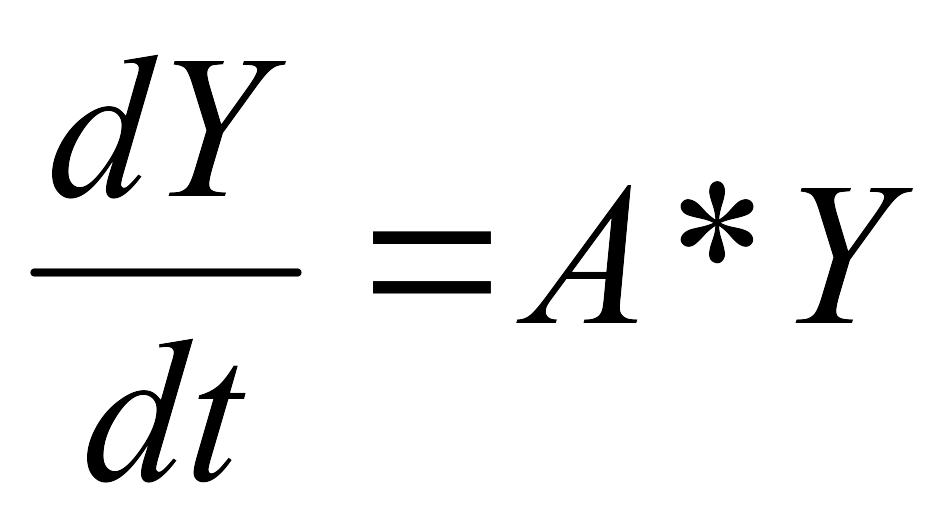, (17)

где A – матрица постоянных коэффициентов, Y – искомый вектор.

Эта система дифференциальных уравнений относится к линейным системам, поскольку в правой части отсутствуют нелинейные слагаемые по искомой функции (нет квадратов, кубов и других нелинейных выражений от Y). Кроме того, эта система относится к однородным системам дифференциальных уравнений, поскольку в правой части отсутствуют свободные слагаемые, зависящие только от аргумента.

Интересной особенностью однородных систем дифференциальных уравнений, как в прочем и однородных систем алгебраических уравнений, является наличие тривиального – нулевого решения – Y(t)=0. Это решение соответствует состоянию покоя (равновесия) моделируемого объекта.

Затухающие колебания

Периодический процесс с затуханием описывается дифференциальным уравнением гармонических колебаний с учетом силы сопротивления. Силу сопротивления можно описать различными способами, в зависимости от ее характера. Рассмотрим возможный вариант силы сопротивления. Скорость изменения моделируемой величины - . Пусть сила сопротивления будет направлена против скорости и пропорциональна скорости изменения по величине, то есть, чем больше скорость изменения, тем больше сила сопротивления, если скорость изменения моделируемой величины равна нулю, тогда и сила сопротивления будет равна нулю. Введем коэффициент пропорциональности силы сопротивления скорости – k, тогда получим выражение для силы сопротивления: