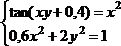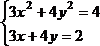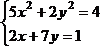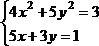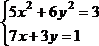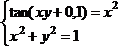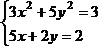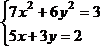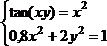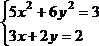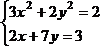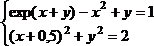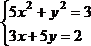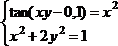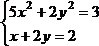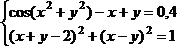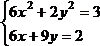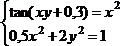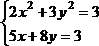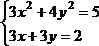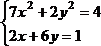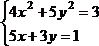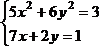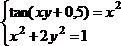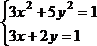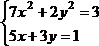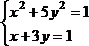Добавлен: 06.11.2018
Просмотров: 2461
Скачиваний: 106
Задание 4. Решение систем линейных алгебраических уравнений.
Для работы с матрицами используем (Вставка функции Математические):
МОБР вычисление обратной матрицы А-1;
МОПРЕД вычисление определителя матрицы D;
МУМНОЖ нахождение произведения двух матриц.
С их помощью можно решать системы линейных алгебраических уравнений вида
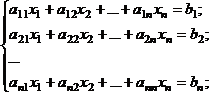 (4.4)
(4.4)
или в матричном виде
А*Х=В,
где А = {aij}– матрица коэффициентов при неизвестных; В = {bij} – вектор-столбец правых частей уравнений; Х = {xij} – вектор-столбец неизвестных.
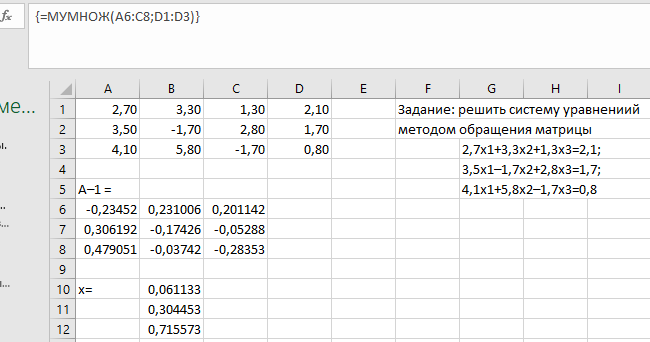
Способ 1 (метод обратной матрицы). Решение имеет вид Х = А–1*В, где А–1 – матрица, обратная по отношению к матрице А.
С помощью функции МОБР находится обратная матрица, а затем с помощью функции МУМНОЖ она перемножается с вектором-столбцом правых частей уравнений.
Напоминание. При работе с матрицами перед вводом формулы необходимо выделить область на рабочем листе, куда будет выведен результат вычисления, а после задания исходных данных в поле функции выйти не как обычно, нажатием клавиши Enter или кнопки ОК, а нажатием клавиш Ctrl + Shift + Enter.
Способ 2 (правило Крамера). Если определитель , составленный из коэффициентов при неизвестных, отличен от нуля, то решение имеет вид
x j = j / , j=1...n. (4.5)
Здесь j – дополнительный определитель, полученный из главного определителя системы путем замены его j-го столбца вектором-столбцом В.
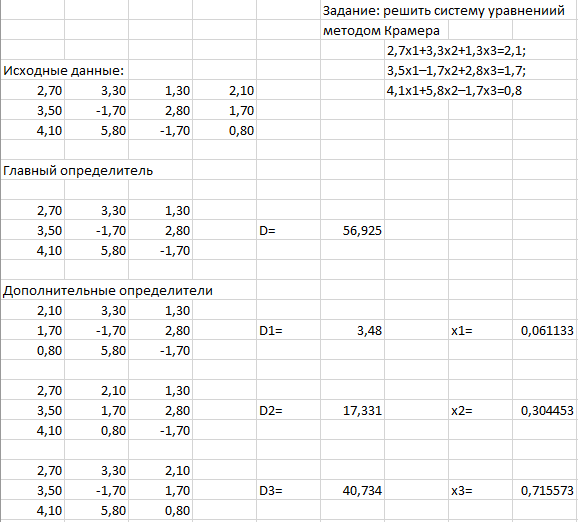
С помощью функции МОПРЕД находятся главный и дополнительные определители, и по формулам (4.5) вычисляются корни СЛАУ.
Способ 3 (метод исключений Гаусса). Этот метод основан на приведении матрицы системы к треугольному виду, что достигается последовательным исключением неизвестных из уравнений системы.
Предположим, что в (4.4) a11 0. Разделим первое уравнение системы на a11 (этот коэффициент называется ведущим или главным элементом), получим
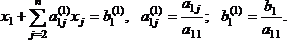
Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент ai1 (i=2,3,, n).
Эти n–1 уравненийпринимаютвид
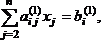
где ![]()
Далее аналогичную процедуру выполняют с этой системой, оставляя в покое первое уравнение. Только теперь делят на другой ведущий элемент a22(1) 0.
В результате исключения неизвестных приходим к СЛАУ с верхней треугольной матрицей с единицами на главной диагонали:
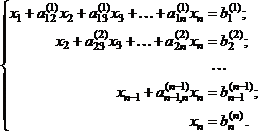 (4.6)
(4.6)
Индексы над коэффициентами означают, сколько раз данное уравнение преобразовывалось.
Прямой ход метода Гаусса завершен.
Обратный ход метода Гаусса заключается в нахождении неизвестных xn, xn-1, ... ,x1 , причем в указанном порядке.
В этом списке xn уже определено из последнего уравнения системы (4.6), а общая формула обратного хода имеет вид:
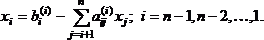
Проиллюстрируем этот алгоритм на примере решения системы из трех уравнений.
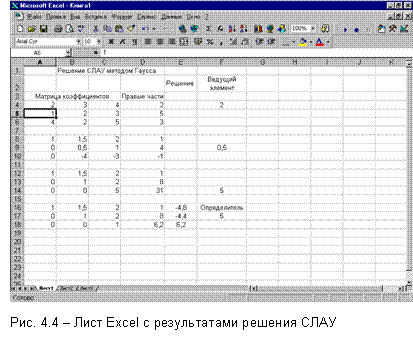
1. Располагаем на листе Excel матрицу коэффициентов и столбец правых частей (т.н. расширенная матрица 34), например, в ячейках А4:D6 (рис. 4.4).
2. Выделяем диапазон ячеек А8:D8 и вводим формулу:
{=A4:D4/A4}.
Фигурные скобки появляются автоматически при вводе формулы комбинацией клавиш Shift+Ctrl+Enter, как признак того, что идет работа не с отдельными ячейками, а с массивами.
3. Выделяем диапазон ячеек А9:D9, вводим формулу
{=A5:D5-$A$8:$D$8*B5}
и копируем эту формулу в диапазон ячеек А10:D10. В ячейках А9 и А10 появились нули.
4. В ячейки А12:D12 копируем значения первой строки расширенной матрицы А8:D8, в ячейки А13:D13 – формулу
{=A9:D9/B9}.
При этом второй элемент главной диагонали матрицы коэффициентов становится равным единице.
|
|
|
|
|
|
В ячейки А14:D14 вводим формулу
{=A10:D10–$A$13:$D$13*B10}.
5) В ячейки А16:D17 копируем значения первых двух строк расширенной матрицы (А12:D13), а в ячейки А18:D18 – формулу
{=A14:D14/C14}.
Прямой ход метода Гаусса завершен: получилась верхняя треугольная матрица с диагональными элементами, равными 1.
Решить тремя способами систему линейных алгебраических уравнений, взяв данные для решения из таблицы 4.3.
Проверить найденное решение умножением матрицы коэффициентов на вектор-столбец решения.
Таблица 4.3 – Системылинейныхалгебраическихуравнений
|
Вариант |
СЛАУ |
Вариант |
СЛАУ |
|
1 |
2,7x1+3,3x2+1,3x3=2,1; 3,5x1–1,7x2+2,8x3=1,7; 4,1x1+5,8x2–1,7x3=0,8 |
2 |
0,34x1+0,71x2+0,63x3=2,08; 0,71x1–0,65x2–0,18x3=0,17; 1,17x1–2,35x2+0,75x3=1,28
|
|
3 |
1,7x1+2,8x2+1,9x3=0,7; 2,1x1+3,4x2+1,8x3=1,1; 4,2x1–3,3x2+1,3x3=2,1 |
4 |
3,75x1–0,28x2+0,17x3=0,75; 2,11x1–0,11x2–0,12x3=1,11; 0,22x1–3,17x2+1,81x3=0,05
|
|
5 |
3,1x1+2,8x2+1,9x3=0,2; 1,9x1+3,1x2+2,1x3=2,1; 7,5x1+3,8x2+4,8x3=5,6
|
6 |
0,21x1–0,18x2+0,75x3=0,11; 0,13x1+0,75x2–0,11x3=2,00; 3,01x1–0,33x2+0,11x3=0,13
|
|
7 |
9,1x1+5,6x2+7,8x3=9,8; 3,8x1+5,1x2+2,8x3=6,7; 4,1x1+5,7x2+1,2x3=5,8
|
8 |
0,13x1–0,14x2–2,00x3=0,15; 0,75x1+0,18x2–0,77x3=0,11; 0,28x1–0,17x2+0,39x3=0,12
|
|
9 |
3,3x1+2,1x2+2,8x3=0,8; 4,1x1+3,7x2+4,8x3=5,7; 2,7x1+1,8x2+1,1x3=3,3
|
10 |
3,01x1–0,14x2–0,15x3=1,00; 1,11x1+0,13x2–0,75x3=0,13; 0,17x1–2,11x2+0,71x3=0,17
|
|
11 |
7,6x1+5,8x2+4,7x3=10,1; 3,8x1+4,1x2+2,7x3=9,7; 2,9x1+2,1x2+3,8x3=7,8
|
12 |
0,92x1–0,83x2+0,62x3=2,15; 0,24x1–0,54x2+0,43x3=0,62; 0,73x1–0,81x2–0,67x3=0,88
|
|
13 |
3,2x1–2,5x2+3,7x3=6,5; 0,5x1+0,34x2+1,7x3=0,2 1,6x1+2,3x2–1,5x3=4,3
|
14 |
1,24x1–0,87x2–3,17x3=0,46; 2,11x1–0,45x2+1,44x3=1,50; 0,48x1+1,25x2–0,63x3=0,35
|
|
15 |
5,4x1–2,3x2+3,4x3=3; 4,2x1+1,7x2–2,3x3=2,7; 3,4x1+2,4x2+7,4x3=1,9
|
16 |
0,64x1–0,83x2+4,2x3=2,23; 0,58x1–0,83x2+1,43x3=1,71; 0,86x1+0,77x2+0,88x3=–0,54
|
|
17 |
3,6x1+1,8x2–4,7x3=3,8; 2,7x1–3,6x2+1,9x3=0,4; 1,5x1+4,5x2+3,3x3=1,6
|
18 |
0,32x1–0,42x2+0,85x3=1,32; 0,63x1–1,43x2–0,58x3=0,44; 0,84x1–2,23x2–0,52x3=0,64
|
Продолжениетаблицы 4.3
|
Вариант |
СЛАУ |
Вариант |
СЛАУ |
|
19 |
5,6x1+2,7x2–1,7x3=1,9; 3,4x1–3,6x2–6,7x3=2,4; 0,8x1+1,3x2+3,7x3=1,2
|
20 |
0,73x1+1,24x2–0,38x3=0,58; 1,25x1+0,66x2–0,78x3=0,66; 0,75x1+1,22x2–0,83x3=0,92
|
|
21 |
2,7x1+0,9x2–1,5x3=3,5; 4,5x1–2,8x2+6,7x3=2,6; 5,1x1+3,7x2–1,4x3=0,14
|
22 |
0,62x1–0,44x2–0,86x3=0,68; 0,83x1+0,42x2–0,56x3=1,24; 0,58x1–0,37x2–0,62x3=0,87
|
|
23 |
4,5x1–3,5x2+7,4x3=2,5; 3,1x1–0,6x2–2,3x3=1,5; 0,8x1+7,4x2–0,5x3=6,4
|
24 |
1,26x1–2,34x2+1,17x3=3,14; 0,75x1+1,24x2–0,48x3=–1,17; 3,44x1–1,85x2+1,16x3=1,83
|
|
25 |
3,8x1+6,7x2–1,2х3=5,2; 6,4x1+1,3x2–2,7x3=3,8; 2,4x1–4,5x2+3,5x3=–0,6
|
26 |
0,46x1+1,72x2+2,53x3=2,44; 1,53x1–2,32x2–1,83x3=2,83; 0,75x1+0,86x2+3,72x3=1,06
|
|
27 |
5,4x1–6,2x2–0,5x3=0,52; 3,4x1+2,3x2+0,8x3=-0,8; 2,4x1–1,1x2+3,8x3=1,8
|
28 |
2,47x1+0,65x2–1,88x3=1,24; 1,34x1+1,17x2+2,54x3=2,35; 0,86x1–1,73x2–1,08x3=3,15
|
|
29 |
7,8x1+5,3x2+4,8x3=1,8; 3,3x1+1,1x2+1,8x3=2,3; 4,5x1+3,3x2+2,8x3=3,4
|
30 |
4,24x1+2,73x2–1,55x3=1,87; 2,34x1+1,27x2+3,15x3=2,16; 3,05x1–1,05x2–0,63x3=–1,25
|
|
31 |
3,8x1+4,1x2–2,3x3=4,8; 2,1x1+3,9x2–5,8x3 = 3,3; 1,8x1+1,1x2–2,1x3=5,8
|
32 |
0,43x1+1,24x2–0,58x3=2,71; 0,74x1+0,83x2+1,17x3=1,26; 1,43x1 - 1,58x2+0,83x3=1,03
|
|
33 |
1,7x1–2,2x2+3,0x3=1,8; 2,1x1+1,9x2–2,3x3=2,8; 4,2x1+3,9x2–3,1x3=5,1
|
34 |
0,43x1+0,63x2+1,44x3=2,18; 1,64x1–0,83x2–2,45x3=1,84; 0,58x1+1,55x2+3,18x3=0,74
|
|
35 |
2,8x1+3,8x2–3,2x3=4,5; 2,5x1–2,8x2+3,3x3=7,1; 6,5x1–7,1x2+4,8x3=6,3
|
36 |
1,24x1+0,62x2–0,95x3=1,43; 2,15x1–1,18x2+0,57x3=2,43; 1,72x1–0,83x2+1,57x3=3,88
|
Продолжениетаблицы 4.3
|
Вариант |
СЛАУ |
Вариант |
СЛАУ |
|
37 |
3,3x1+3,7x2+4,2x3=5,8; 2,7x1+2,3x2–2,9x3=6,1; 4,1x1+4,8x2–5,0x3=7,0
|
38 |
0,62x1+0,56х2–0,43x3=1,16; 1,32x1–0,88x2+1,76x3=2,07; 0,73x1+1,42x2–0,34x3=2,18
|
|
39 |
7,1x1+6,8x2+6,1x3=7,0; 5,0x1+4,8x2+5,3x3=6,1; 8,2x1+7,8x2+7,1x3=5,8
|
40 |
1,06x1+0,34x2+1,26x3=1,17; 2,54x1–1,16x2+0,55x3=2,23; 1,34x1–0,47x2–0,83x3=3,26
|
Задание 5. Решение систем нелинейных уравнений.
С помощью сервисной программы Поиск решения (Сервис | Поиск решения) в Excel можно решать системы нелинейных уравнений.
В общем случае система нелинейных уравнений имеет вид:
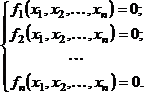 (4.7)
(4.7)
Составим новую функцию F(x1, х2, ..., хn), представляющую собой сумму квадратов правых частей уравнений:
![]() . (4.8)
. (4.8)
Очевидно, переменные x1, х2, ..., хn , являющиеся решением системы (4.7), с необходимостью и достаточностью являются также решением уравнения
![]() . (4.9)
. (4.9)
Путь решения следующий.
На листе Excel отводим ячейки для неизвестных данной системы уравнений, например с А1 по А5 (если пять переменных), и вводим туда начальные приближения. В ячейку В2 вводим формулу, вычисляющую функцию (4.8).
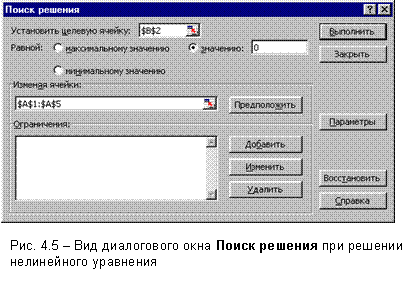
Открываем диалоговое окно Поиск решения (рис. 4.5). В поле Установить целевую ячейку вводим В2, в группе Равной устанавливаем переключатель в положение Значению и в поле ввода задаем 0. В поле Изменяя ячейки вводимдиапазонячеек А1:А5.
|
|
|
|
|
|
После нажатия на кнопку Выполнить будет найдено решение, которое поместится в ячейки А1:А5. В ячейке В2 будет вычислено значение левой части уравнения (4.9) с относительной погрешностью, задаваемой в диалоговом окне Параметры поиска решения .
Примечание 1. При неудачном выборе вектора начального приближения решение может быть не найдено. Поэтому необходим предварительный анализ системы уравнений с целью определения лучшего (более близкого к корню) начального приближения. Например, для системы из двух уравнений можно затабулировать функцию (4.8) и в качестве начальных выбрать приближения, наиболее близкие к нулю.
Примечание 2. Система уравнений может иметь несколько корней, поэтому необходим ее анализ и с этой стороны. Задавая разные начальные приближения, можно получить разные решения системы.
Примечание 3. Более подробно о возможностях программы Поиск решения изложено в лабораторной работе 12.
tan(ху+0,4)-x2 +0,6 x2 + 2 y2-1
Решить систему нелинейных уравнений, взяв данные из таблицы 4.4. Проверитьнайденноерешение.
Таблица 4.4 – Системынелинейныхуравнений
|
Вариант |
СНУ |
Вариант |
СНУ |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
Продолжениетаблицы 4.4
|
Вариант |
СНУ |
Вариант |
СНУ |
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
|
31 |
|
32 |
|
|
33 |
|
34 |
|
|
35 |
|
36 |
|
|
37 |
|
38 |
|
|
39 |
|
40 |
|
Построить поверхность, описываемую функцией F(x, y) в окрестности одного из корней, пользуясь описанием, приведенным в лабораторной работе 2.
Пример1 решения уравнения, используя надстройку “Поиск решения”
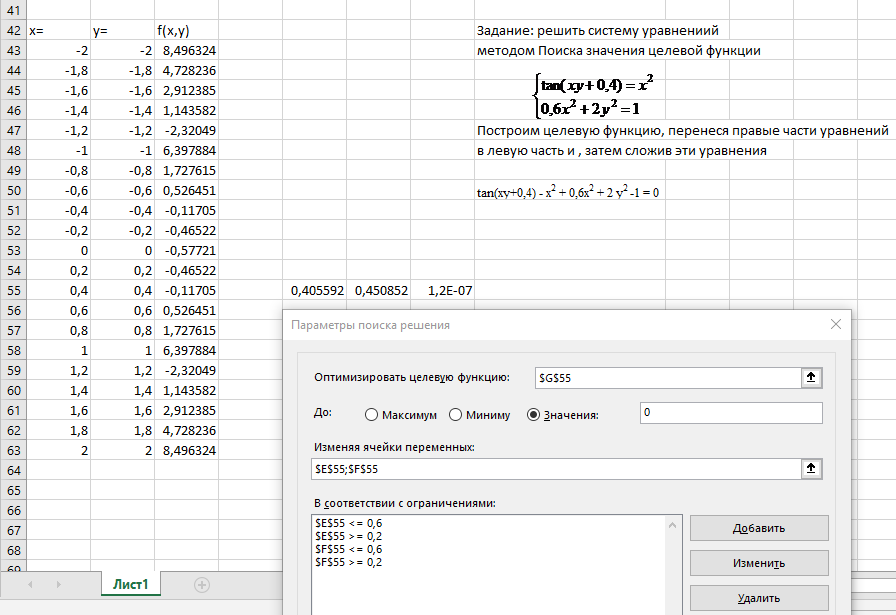
Например, найдем все корни уравнения 2x3-15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3;3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня. На рисунке 12 представлен пример заполнения окна Поиск решения для нахождения первого корня на отрезке [-2; -1].
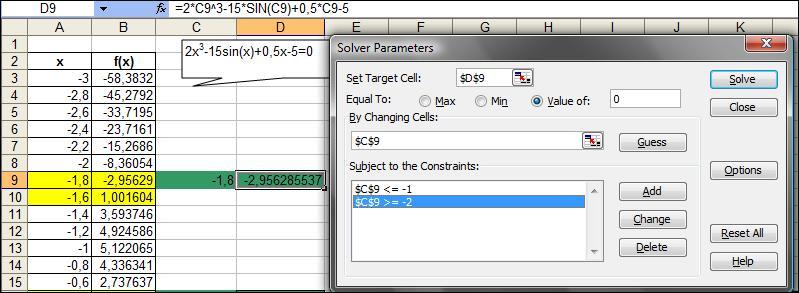
Рисунок 8. Пример решения уравнения при помощи надстройки Поиск решения
Рисунок 9. Пример2 решения уравнения при помощи надстройки Поиск решения