Файл: Двойные углы 3 Sin2X Рассмотрим выражение sin2x представим его аргумент в виде 2xxx и воспользуемся известной формулой синуса суммы аргументов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 138
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вопрос 1
1)Теорема синусов:
2)Теорема Косинусов
Двойные углы
3)Sin2X:
Рассмотрим выражение sin2x — представим его аргумент в виде 2x=x+x и воспользуемся известной формулой синуса суммы аргументов:
sin(α+β)=sinα⋅cosβ+cosα⋅sinβ.
Тогда получим:
sin2x=sin(x+x)=sinx⋅cosx+cosx⋅sinx=2sinx⋅cosx.
4)Cos2X:
Рассмотрим выражение cos2x и аналогично представим его аргумент в виде 2x=x+x, а также воспользуемся известной формулой косинуса суммы аргументов:
cos(α+β)=cosα⋅cosβ−sinα⋅sinβ.
Тогда получим:
cos2x=cos(x+x)=cosx⋅cosx−sinx⋅sinx=cos2x−sin2x.
5)
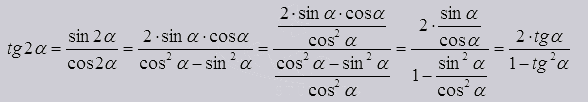
6)
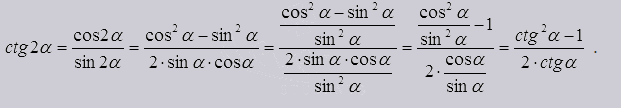
Тройные углы
7)

8)

9)
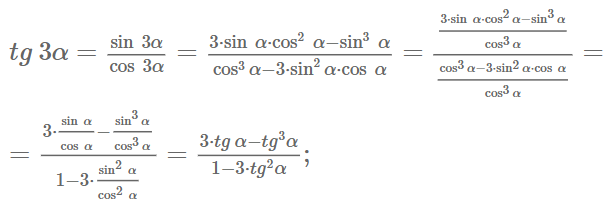
10)
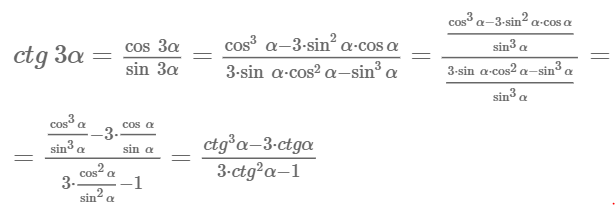
Вопрос 2
Sin:
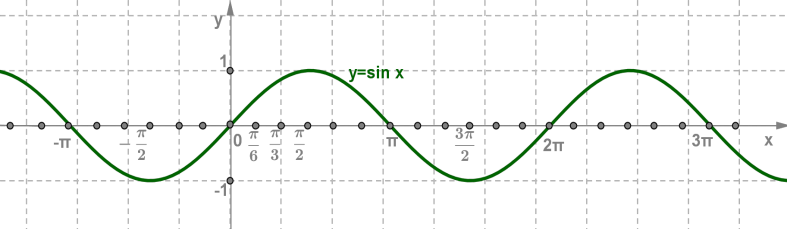
1. Область определения — множество всех действительных чисел.
2. Множество значений — отрезок [−1;1].
3. Функция y=sinx периодическая с периодом T= 2π.
4. Функция y=sinx — нечётная.
5. Функция y=sinx принимает:
- значение, равное 0, при x=πn,n∈Z;
- наибольшее значение, равное 1, при x=π2+2πn,n∈Z;
- наименьшее значение, равное −1, при x=−π2+2πn,n∈Z;
- положительные значения на интервале (0;π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z;
- отрицательные значения на интервале (π;2π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z.
6. Функция y=sinx:
- возрастает на отрезке
[−π2;π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z;
- убывает на отрезке
[π2;3π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z.
7.Асимптот нет
Cos:
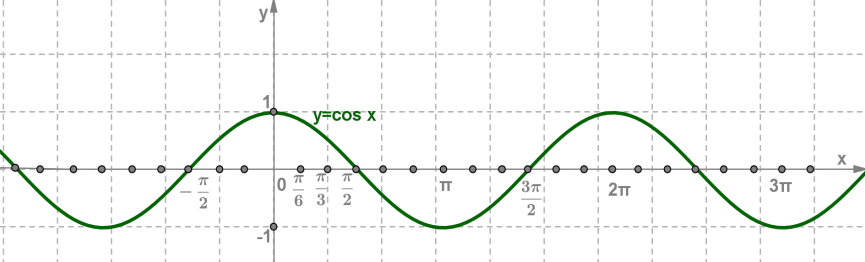
1. Область определения — множество R всех действительных чисел.
2. Множество значений — отрезок [−1;1].
3. Функция y=cosx периодическая с периодом 2π.
4. Функция y=cosx — чётная.
5. Функция y=cosx принимает:
- значение, равное 0, при x=π2+πn,n∈Z;
- наибольшее значение, равное 1, при x=2πn,n∈Z;
- наименьшее значение, равное −1, при x=π+2πn,n∈Z;
- положительные значения на интервале (−π2;π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z;
- отрицательные значения на интервале (π2;3π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z.
6. Функция y=cosx:
- возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z;
- убывает на отрезке [0;π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z.
7.Асимптот нет
Tg
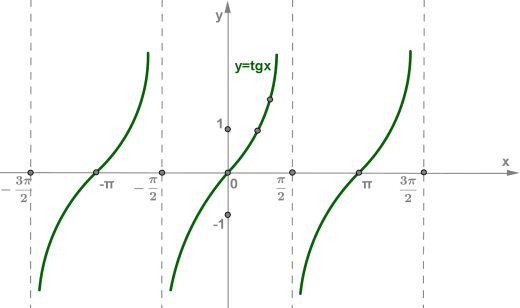
1. Область определения — множество всех действительных чисел x≠π2+πn,n∈Z
2. Множество значений — множество R всех действительных чисел.
3. Функция y=tgx периодическая с периодом π.
4. Функция y=tgx нечётная.
5. Функция y=tgx принимает:
- значение 0 при x=πn,n∈Z;
- положительные значения на интервалах (πn;π2+πn),n∈Z;
- отрицательные значения на интервалах (−π2+πn;πn),n∈Z.
6. Функция y=tgx возрастает на интервалах (−π2+πn;π2+πn),n∈Z.
7/Так как данная функция имеет разрыв
в точках x= , то
Следовательно, ,
Ctg
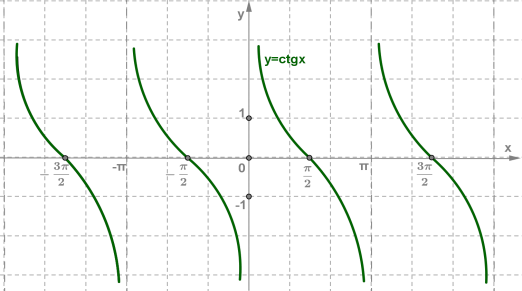
1. Область определения — множество всех действительных чисел x≠πn,n∈Z.
2. Множество значений — множество R всех действительных чисел.
3. Функция y=ctgx периодическая с периодом π.
4. Функция y=ctgx нечётная.
5. Функция y=ctgx принимает:
- значение 0 при x=π2+πn,n∈Z;
- положительные значения на интервалах (πn;π2+πn),n∈Z;
- отрицательные значения на интервалах (−π2+πn;πn),n∈Z.
6. Функция y=ctgx убывает на интервалах (πn;π+πn),n∈Z.
7.x = πn
Вопрос 3
ArcSin:
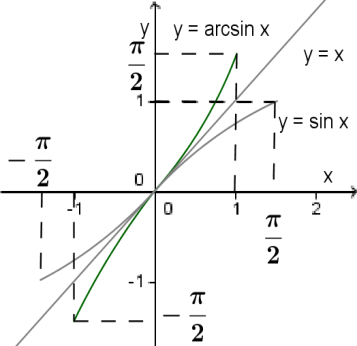
1. Область определения — отрезок [−1;1].
2. Множество значений — отрезок [−π2;π2].
3. Функция y=arcsinx — возрастает.
4. Функция y=arcsinx является нечётной, так как arcsin(−x)=−arcsinx.
5.Асимптот нет
ArcCos:
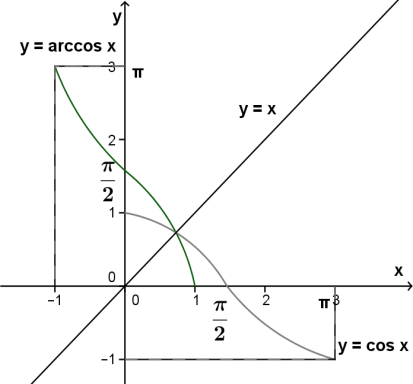
1. Область определения — отрезок [−1;1].
2. Множество значений — отрезок [0;π].
3. Функция y=arccosx убывает.
4.Асимптот не
ArcTg:
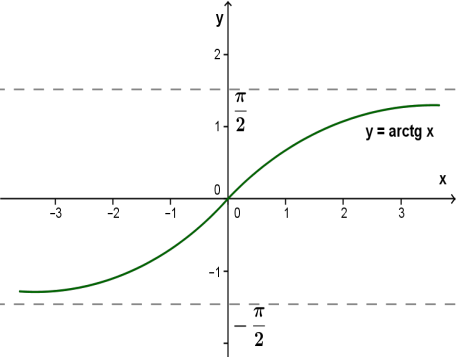
1. Область определения — множество R всех действительных чисел.
2. Множество значений — интервал (−π2;π2).
3. Функция y=arctgx возрастает.
4. Функция y=arctgx является нечётной, так как arctg(−x)=−arctgx.
5.Асимптота
ArcCtg:
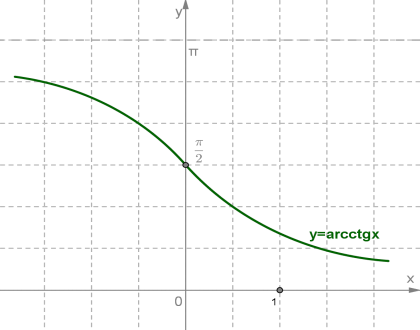
1. D(f)=(−∞;+∞).
2. E(f)=(0;π).
3. Функция не является ни чётной, ни нечётной, т. к. график функции не симметричен ни относительно начала координат, ни относительно оси y.
4. Функция убывает.
5. Функция непрерывна.
6.Асимптота y = 0
Вопрос 4
1) векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами.
три вектора называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.
2) Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
3) Линейными операциями над векторами называются операции сложения (вычитания) векторов и умножения вектора на число
Свойства: 1)Проеция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:
Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта
O оси l. Так как координата проекции начала равна нулю, то обозначим .
2) Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: .
Доказательство. Пусть . Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда .
Но
Это свойство можно обобщить на случай любого числа слагаемых.
3)Если вектор умножается на число λ, то его проекция на ось также умножается на это число:
.
Доказательство. Пусть угол между вектором и осью .
Если λ > 0, то вектор имеет то же направление, что и , и составляет с осью такой же угол .
При λ > 0
Если же λ < 0, то и имеют противоположные направления и вектор составляет с осью угол π – φ и
Вопрос 5
1)Проекции вектора на оси координат называются его координатами. В этом заключается их геометрический смысл.
Если задана система координат на плоскости и в пространстве, то начало вектора можно всегда совместить с началом координат, не меняя при этом длину и направление. Выделим на координатных осях единичные векторы и обозначим
Проведем через конец вектора плоскости, параллельные координатным плоскостям. Точки пересечения с осями обозначим соответственно через М1,М2,М3. Получили прямоугольный параллелепипед, одной диагональю которого является
2) Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB
3) Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.
4)Линейные операции над векторами
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
1) а ± b = (ах ±bх)i + (ау ±by)j + ( az ± bz)k, или кратко а ± b = (ах ±bx; ay± by; az± bz). To есть при сложении (вычитании) векторових одноименные координаты складываются (вычитаются).
2) l а = l ах • i + l ау • j + l az • k или короче l а = (lах; lау; lаz). То естьпри умножении вектора на скаляр координаты вектора умножаются на этот скаляр.