Файл: Двойные углы 3 Sin2X Рассмотрим выражение sin2x представим его аргумент в виде 2xxx и воспользуемся известной формулой синуса суммы аргументов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 150
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- являются асимптотами гиперболы. (чертеж 19.) [1.С.108]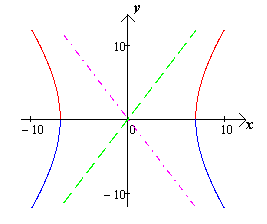
4) Фокусы гиперболы:
Пусть фокусы гиперболы лежат на оси Ох. Межфокусное расстояние гиперболы равно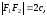
причем 
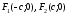. Заметим, что по определению гиперболы.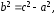 
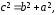
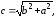
Следовательно,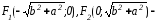
фокусы гиперболы. [1.С.109]
5) Директориальное свойство гиперболы: Определение 3.4. Директрисами гиперболы называются прямые, параллельные канонической оси ОУ и отстоящие от этой оси на расстояние .
Уравнения директрис гиперболы имеют вид: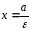
и
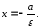[5.С.122]
6) Эксцентриситет гиперболы: Определение 3.5. Отношение называется эксцентриситетом гиперболы. Так как , то
Е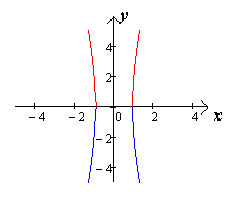
сли при постоянном значении , число будет изменяться от нуля до бесконечности, то 
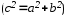будет измениться от до бесконечности. Если , то гипербола будет стремиться к лучам (чертеж 20.).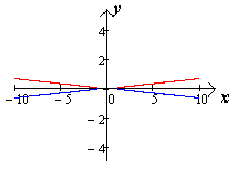
Если , то гипербола будет стремиться к параллельным прямым (чертеж 21.). [1.С.109]
Определение. Параболой называется геометрическое место точек плоскости для которых расстояние до фокуса равно расстоянию до некоторой прямой, называемой директрисой.
Для вывода уравнения параболы зафиксируем систему координат ХОу, как показано на рисунке, и обозначим расстояние от фокуса до директрисы через
С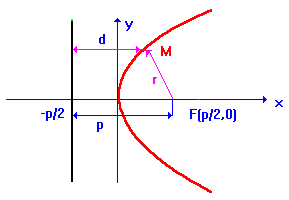
огласно определению параболы имеем , или в координатах .
Возведем обе части уравнения в квадрат, приведем подобные члены, получим каноническое уравнение параболы , (1)
Где называется Параметром Параболы.
2 Из уравнения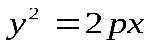
следует, что может принимать положительные значения и ноль. Значит, вся парабола располагается по одну сторону от оси 
. Так как уравнение содержит только чётную степень переменной у, то парабола симметрична относительно оси 
, и для выяснения её формы достаточно рассмотреть только I четверть, где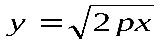 
. Ось называется осью симметрии параболы (ось параболы).
П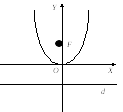
арабола проходит через точку (0,0).
a)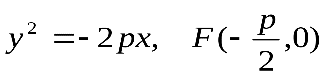
б)
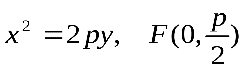
в)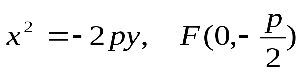 
Определение 11.2. Величина р, фигурирующая в уравнении параболы, называется фокальным параметром параболы.Фокальный параметр имеет следующее геометрическое истолкование: если через фокус параболы провести прямую, перпендикулярную оси параболы, и найти точки пересечения этой прямой с параболой, то при совместном решении системы уравнений: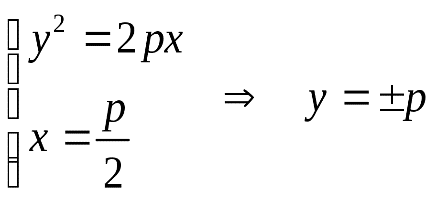
, т. е.
.
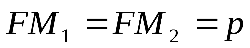Таким образом, фокальный параметр равен длине перпендикуляра, проведенного из фокуса до точки пересечения с параболой. Фокальный параметр характеризует форму и размеры параболы. Он изменяется от 0 до . Чем больше фокальный параметр, тем парабола сильнее вытягивается вдоль оси .
3) Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки
этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в рассматриваемой плоскости.
Прямая, о которой идет речь в определении, называется директрисой параболы.
Директриса параболы, определяемой каноническим уравнением, имеет уравнение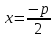
4)Фокус – «центр этой хуйни»
5) Если дана квадратичная функция y=ax2+bx+c, где a,b,c ∈ R и a≠0, то абсциссу вершины параболы (xo;yo) можно вычислить по формуле: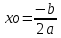
.
6)Расстояние от точки на параболе, до фокуса = фокальный радиус = X вершины параболы + P/2
1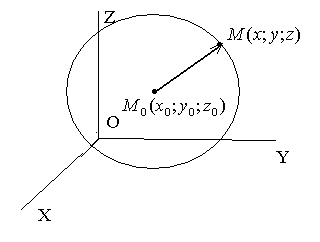
)Пусть сфера имеет радиус 
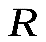, а ее центр находится в точке 
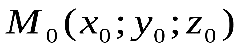. Точка 
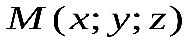лежит на сфере тогда и только тогда, когда модуль вектора
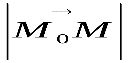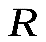равен , то есть
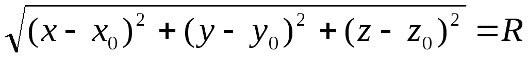. А последнее равенство выполнено тогда и только тогда, когда
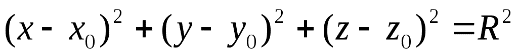(1)
Уравнение (1) и является искомым уравнением сферы.
2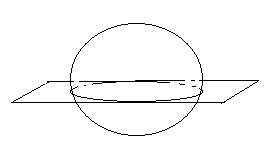
)В аналитической геометрии в пространстве каждая линия рассматривается как пересечение двух поверхностей и соответственно этому определяется заданием двух уравнений.
Например. Окружность в пространстве задается как пересечение сферы:
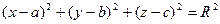и плоскости 
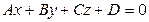(рис.13)
Рис.13
Если и уравнения двух поверхностей, пересекающихся по некоторой линии L, то линия L есть геометрическое место общих точек этих поверхностей, то есть точек координаты которых удовлетворяют одновременно и уравнению и .
Линия в пространстве задаётся в общем случае как линия пересечения некоторых поверхностей и . Система уравнений:
н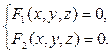
азывается уравнением линии в пространстве.
Общее уравнение плоскости: Любую плоскость, заданную в прямоугольной системе координат OxyzOxyz трехмерного пространства, можно определить уравнением Ax + By + Cz + D = 0. В свою очередь, любое уравнение Ax + By + Cz + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A, B, C, D– некоторые действительные числа, и числа A, B, C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида Ax + By + Cz + D = 0 Допустим, задана некоторая плоскость и точка M0(x0, y0, z0) через которую эта плоскость проходит. Нормальным вектором этой плоскости является n= (A, B, C). Приведем доказательство, что указанную плоскость в прямоугольной системе координат Oxyz задает уравнение Ax + By + Cz + D = 0.
Возьмем произвольную точку заданной плоскости M(x, y, z) В таком случае векторы n= (A, B, C) и M0M=(x−x0, y−y0, z−z0) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
(n, M0M)=A(x−x0)+B(y−y0)+C(z−z0)=Ax+By+Cz−(Ax0+By0+Cz0)
Примем D=−(Ax0+By0+Cz0), тогда уравнение преобразуется в следующий вид: Ax + By + Cz + D = 0. Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
Во второй части теоремы утверждается, что любое уравнение вида Ax + By + Cz + D = 0 задает некоторую плоскость в прямоугольной системе координат Oxyz трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А, B, C одновременно не являются равными нулю. Тогда существует некоторая точка M0(x0, y0, z0), координаты которой отвечают уравнению Ax + By + Cz + D = 0, т.е. верным будет равенство Ax0 + By0 + Cz0 + D = 0.
Отнимем левую и правую части этого равенства от левой и правой частей уравнения Ax + By + Cz + D = 0. Получим уравнение вида
A(x−x0) + B(y−y0) + C(z−z0) + D = 0, и оно эквивалентно уравнению Ax + By + Cz + D = 0. Докажем, что уравнение A(x−x0) + B(y−y0) + C(z−z0) + D = 0 задает некоторую плоскость.
Уравнение A(x−x0) + B(y−y0) + C(z−z0) + D = 0
4) Фокусы гиперболы:
Пусть фокусы гиперболы лежат на оси Ох. Межфокусное расстояние гиперболы равно
причем . Заметим, что по определению гиперболы. Следовательно,
фокусы гиперболы. [1.С.109]5) Директориальное свойство гиперболы: Определение 3.4. Директрисами гиперболы называются прямые, параллельные канонической оси ОУ и отстоящие от этой оси на расстояние .
Уравнения директрис гиперболы имеют вид:
и [5.С.122]6) Эксцентриситет гиперболы: Определение 3.5. Отношение называется эксцентриситетом гиперболы. Так как , то
Е
сли при постоянном значении , число будет изменяться от нуля до бесконечности, то будет измениться от до бесконечности. Если , то гипербола будет стремиться к лучам (чертеж 20.). Если , то гипербола будет стремиться к параллельным прямым (чертеж 21.). [1.С.109]
Вопрос 17
Определение. Параболой называется геометрическое место точек плоскости для которых расстояние до фокуса равно расстоянию до некоторой прямой, называемой директрисой.
Для вывода уравнения параболы зафиксируем систему координат ХОу, как показано на рисунке, и обозначим расстояние от фокуса до директрисы через
С
огласно определению параболы имеем , или в координатах .Возведем обе части уравнения в квадрат, приведем подобные члены, получим каноническое уравнение параболы , (1)
Где называется Параметром Параболы.
2 Из уравнения
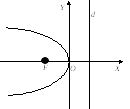следует, что может принимать положительные значения и ноль. Значит, вся парабола располагается по одну сторону от оси . Так как уравнение содержит только чётную степень переменной у, то парабола симметрична относительно оси , и для выяснения её формы достаточно рассмотреть только I четверть, где . Ось называется осью симметрии параболы (ось параболы). П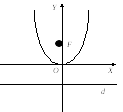 арабола проходит через точку (0,0).a)
б)
в) Определение 11.2. Величина р, фигурирующая в уравнении параболы, называется фокальным параметром параболы.Фокальный параметр имеет следующее геометрическое истолкование: если через фокус параболы провести прямую, перпендикулярную оси параболы, и найти точки пересечения этой прямой с параболой, то при совместном решении системы уравнений:
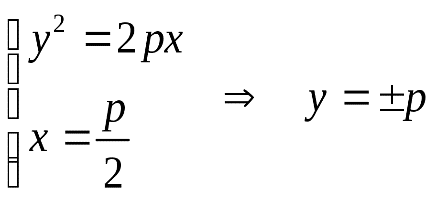, т. е. .Таким образом, фокальный параметр равен длине перпендикуляра, проведенного из фокуса до точки пересечения с параболой. Фокальный параметр характеризует форму и размеры параболы. Он изменяется от 0 до . Чем больше фокальный параметр, тем парабола сильнее вытягивается вдоль оси
.3) Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки
этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в рассматриваемой плоскости.Прямая, о которой идет речь в определении, называется директрисой параболы.
Директриса параболы, определяемой каноническим уравнением, имеет уравнение
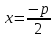
4)Фокус – «центр этой хуйни»
5) Если дана квадратичная функция y=ax2+bx+c, где a,b,c ∈ R и a≠0, то абсциссу вершины параболы (xo;yo) можно вычислить по формуле:
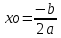. 6)Расстояние от точки на параболе, до фокуса = фокальный радиус = X вершины параболы + P/2
Вопрос 18
1
)Пусть сфера имеет радиус , а ее центр находится в точке . Точка лежит на сфере тогда и только тогда, когда модуль вектора равен , то есть . А последнее равенство выполнено тогда и только тогда, когда (1)Уравнение (1) и является искомым уравнением сферы.
2
)В аналитической геометрии в пространстве каждая линия рассматривается как пересечение двух поверхностей и соответственно этому определяется заданием двух уравнений.Например. Окружность в пространстве задается как пересечение сферы:
и плоскости (рис.13)Рис.13
Если и уравнения двух поверхностей, пересекающихся по некоторой линии L, то линия L есть геометрическое место общих точек этих поверхностей, то есть точек координаты которых удовлетворяют одновременно и уравнению и .
Линия в пространстве задаётся в общем случае как линия пересечения некоторых поверхностей и . Система уравнений:
н
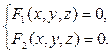азывается уравнением линии в пространстве.Вопрос 19
Общее уравнение плоскости: Любую плоскость, заданную в прямоугольной системе координат OxyzOxyz трехмерного пространства, можно определить уравнением Ax + By + Cz + D = 0. В свою очередь, любое уравнение Ax + By + Cz + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A, B, C, D– некоторые действительные числа, и числа A, B, C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида Ax + By + Cz + D = 0 Допустим, задана некоторая плоскость и точка M0(x0, y0, z0) через которую эта плоскость проходит. Нормальным вектором этой плоскости является n= (A, B, C). Приведем доказательство, что указанную плоскость в прямоугольной системе координат Oxyz задает уравнение Ax + By + Cz + D = 0.
Возьмем произвольную точку заданной плоскости M(x, y, z) В таком случае векторы n= (A, B, C) и M0M=(x−x0, y−y0, z−z0) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
(n, M0M)=A(x−x0)+B(y−y0)+C(z−z0)=Ax+By+Cz−(Ax0+By0+Cz0)
Примем D=−(Ax0+By0+Cz0), тогда уравнение преобразуется в следующий вид: Ax + By + Cz + D = 0. Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
Во второй части теоремы утверждается, что любое уравнение вида Ax + By + Cz + D = 0 задает некоторую плоскость в прямоугольной системе координат Oxyz трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А, B, C одновременно не являются равными нулю. Тогда существует некоторая точка M0(x0, y0, z0), координаты которой отвечают уравнению Ax + By + Cz + D = 0, т.е. верным будет равенство Ax0 + By0 + Cz0 + D = 0.
Отнимем левую и правую части этого равенства от левой и правой частей уравнения Ax + By + Cz + D = 0. Получим уравнение вида
A(x−x0) + B(y−y0) + C(z−z0) + D = 0, и оно эквивалентно уравнению Ax + By + Cz + D = 0. Докажем, что уравнение A(x−x0) + B(y−y0) + C(z−z0) + D = 0 задает некоторую плоскость.
Уравнение A(x−x0) + B(y−y0) + C(z−z0) + D = 0