Файл: Двойные углы 3 Sin2X Рассмотрим выражение sin2x представим его аргумент в виде 2xxx и воспользуемся известной формулой синуса суммы аргументов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 151
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
являет собой условие,
необходимое и достаточное для перпендикулярности векторов n=(A, B, C) и M0M=(x−x0, y−y0, z−z0). Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A(x−x0) + B(y−y0) + C(z−z0) + D = 0 множество точек M(x, y, z)задает плоскость,
у которой нормальный вектор n=(A, B, C). При этом плоскость проходит через точку M(x0, y0, z0).
Иначе говоря, уравнение A(x−x0) + B(y−y0) + C(z−z0) + D = 0 задает в прямоугольной системе координат Oxyz трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение Ax + By + Cz + D = 0 также определяет эту плоскость.
Теорема доказана полностью.
Теорема плоскости в отрезках:
Уравнение плоскости в отрезках
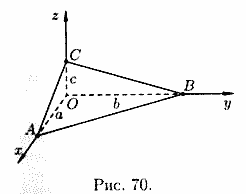
Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a, b и c, т. е. проходит через три точки A(a;0;0), B(0;b;0) и C(0;0;c)(см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем
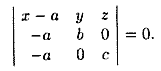
Раскрыв определитель, имеем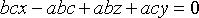 , т. е.
, т. е.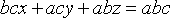
 или
или
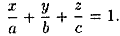 (12.7)
(12.7)
Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.
1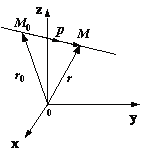 )Векторное уравнение прямой:Пусть для прямой
)Векторное уравнение прямой:Пусть для прямой 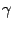 известны ее направляющий вектор
известны ее направляющий вектор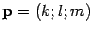 и точка
и точка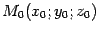 , лежащая на этой прямой. Пусть
, лежащая на этой прямой. Пусть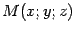 произвольная (текущая) точка прямой
произвольная (текущая) точка прямой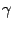 . Обозначим через
. Обозначим через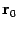 и r радиус-векторы точек
и r радиус-векторы точек 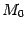 и
и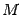 соответственно.
соответственно.
Тогда вектор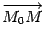 коллинеарен вектору p и, следовательно,
коллинеарен вектору p и, следовательно, 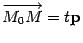 , где
, где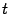 -- некоторое число.
-- некоторое число.
видно, что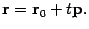
Это уравнение называется векторным уравнением прямой или уравнением в векторной форме. При каждом значении параметра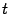 мы будем получать новую точку
мы будем получать новую точку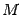 на прямой
на прямой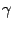 .
.
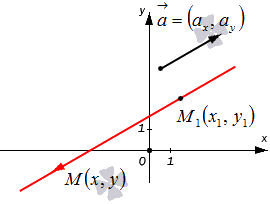
2)Параметрические уравнения прямой: Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.
Допустим, нам задана прямоугольная система координат Oxy. А также заданы прямая а с указанием лежащей на ней точкиМ1(x1, y1) и направляющий вектор заданной прямой a= (ax, ay). Дадим описание заданной прямой a, используя уравнения.
Используем произвольную точку М (x, y) и получим вектор М1М→;
вычислим его координаты по координатам точек начала и конца: M1M=(x-x1, y-y1).
Опишем полученное: прямая задана множеством точек М (x, y), проходит через точку М1(x1, y1)и имеет направляющий вектор a= (ax, ay). Указанное множество задает прямую только тогда, когда векторы M1M→=(x-x1, y-y1) и a= (ax, ay) являются коллинеарными. Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов −−−→M1M=(x−x1, y−y1)M1M→=(x-x1, y-y1) и →a= (ax, ay)a→= (ax, ay) возможно записать в виде уравнения:
−−−→M1M=λ⋅→aM1M→=λ·a→, где λλ – некоторое действительное число.
1)Каноническое уравнение прямой
Определение. Любой вектор, отличный от нулевого, параллельный заданной прямой, называется направляющим вектором этой прямой.
Пусть на прямой задана точка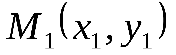 , а вектор
, а вектор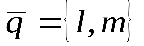 – направляющий вектор прямой . Точка
– направляющий вектор прямой . Точка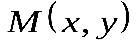 принадлежит прямой, если вектор
принадлежит прямой, если вектор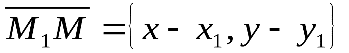 параллелен вектору :
параллелен вектору : 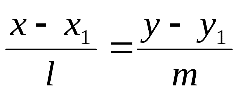 . (12)
. (12)
Уравнение (12) называется каноническим уравнением прямой на плоскости.
Угол между прямыми, заданными каноническими уравнениями, определяется как угол между направляющими векторами этих прямых:
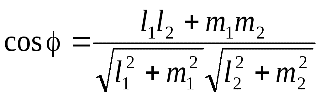 .
.
Условием параллельности прямых будет условие коллинеарности их направляющих векторов:
||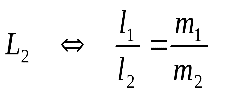 .
.
Условие перпендикулярности прямых равносильно условию равенства нулю скалярного произведения их направляющих векторов:
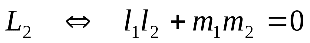 .
.
2) Уравнение прямой в пространстве, проходящей через две точки.
Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) и M2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой: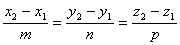 .
.
Кроме того, для точки М1 можно записать: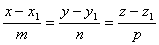 .
.
Решая совместно эти уравнения, получим: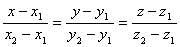 .
.
Это уравнение прямой, проходящей через две точки в пространстве.
3)Общее уравнения прямой
Если на плоскости введена ПДСК, то всякое уравнение первой степени относительно текущих координат и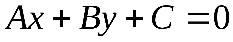 , (5)
, (5)
где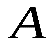 и одновременно не равны нулю, определяет прямую.
и одновременно не равны нулю, определяет прямую.
Верно и обратное утверждение: в ПДСК любая прямая может быть задана уравнением первой степени вида (5).
Уравнение вида (5) называется общим уравнением прямой. Частные случаи уравнения (5) приведены в следующей таблице
34. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.
Под углом между плоскостями понимается один из двугранных углов, образованных этими плоскостями.
Угол между нормальными векторами =(A ;B ; C ) и =(A2;B2; C2) плоскостейQ1иQ2 равен углу между этими плоскостями. Поэтому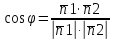
или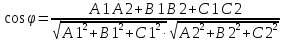 .
.
Пример: Заданы две плоскости и(ABM): -4x-5y+5z-12=0.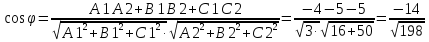
Для нахождения острого угла следует взять модуль правой части.
Если плоскости перпендикулярны, то их нормальные вектора тоже будут перпендикулярны, т. е.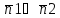 . Но тогда
. Но тогда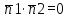 , т. е.
, т. е.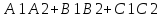 =0. Это равенство есть условие перпендикулярности двух плоскостей.
=0. Это равенство есть условие перпендикулярности двух плоскостей.
Если плоскости параллельны, то будут параллельны и их нормали и . Тогда координаты векторов пропорциональны:
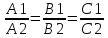 . Это есть условие параллельности двух плоскостей.
. Это есть условие параллельности двух плоскостей.
1)Угол между прямыми: Пересекающиеся прямые l и l1 образуют две пары вертикальных углов. В этом случае углом между прямыми называют один из пары меньших вертикальных углов.
Если прямые скрещиваются (l2 и l3 ), то в углом между прямыми называется угол между пересекающимися прямыми (l2 и m ), который получается в результате параллельного переноса одной из прямых ( l3 ) так, чтобы она пересекала вторую прямую.
В обоих случаях, угол между прямыми равен углу между направляющими векторами этих прямых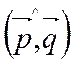 или 1800 -
или 1800 - 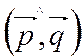 .
.
Пусть направляющие вектора прямых заданы своими координатами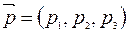 и
и 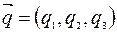 .
.
Тогда для вычисления величины угла между прямыми получаем формулу:
необходимое и достаточное для перпендикулярности векторов n=(A, B, C) и M0M=(x−x0, y−y0, z−z0). Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A(x−x0) + B(y−y0) + C(z−z0) + D = 0 множество точек M(x, y, z)задает плоскость,
у которой нормальный вектор n=(A, B, C). При этом плоскость проходит через точку M(x0, y0, z0).
Иначе говоря, уравнение A(x−x0) + B(y−y0) + C(z−z0) + D = 0 задает в прямоугольной системе координат Oxyz трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение Ax + By + Cz + D = 0 также определяет эту плоскость.
Теорема доказана полностью.
Теорема плоскости в отрезках:
Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a, b и c, т. е. проходит через три точки A(a;0;0), B(0;b;0) и C(0;0;c)(см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем

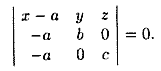
Раскрыв определитель, имеем
Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.
Вопрос 21
1
 )Векторное уравнение прямой:Пусть для прямой
)Векторное уравнение прямой:Пусть для прямой Тогда вектор
видно, что
Это уравнение называется векторным уравнением прямой или уравнением в векторной форме. При каждом значении параметра

2)Параметрические уравнения прямой: Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.
Допустим, нам задана прямоугольная система координат Oxy. А также заданы прямая а с указанием лежащей на ней точкиМ1(x1, y1) и направляющий вектор заданной прямой a= (ax, ay). Дадим описание заданной прямой a, используя уравнения.
Используем произвольную точку М (x, y) и получим вектор М1М→;
вычислим его координаты по координатам точек начала и конца: M1M=(x-x1, y-y1).
Опишем полученное: прямая задана множеством точек М (x, y), проходит через точку М1(x1, y1)и имеет направляющий вектор a= (ax, ay). Указанное множество задает прямую только тогда, когда векторы M1M→=(x-x1, y-y1) и a= (ax, ay) являются коллинеарными. Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов −−−→M1M=(x−x1, y−y1)M1M→=(x-x1, y-y1) и →a= (ax, ay)a→= (ax, ay) возможно записать в виде уравнения:
−−−→M1M=λ⋅→aM1M→=λ·a→, где λλ – некоторое действительное число.
1)Каноническое уравнение прямой
Определение. Любой вектор, отличный от нулевого, параллельный заданной прямой, называется направляющим вектором этой прямой.
Пусть на прямой задана точка
Уравнение (12) называется каноническим уравнением прямой на плоскости.
Угол между прямыми, заданными каноническими уравнениями, определяется как угол между направляющими векторами этих прямых:
Условием параллельности прямых будет условие коллинеарности их направляющих векторов:
||
Условие перпендикулярности прямых равносильно условию равенства нулю скалярного произведения их направляющих векторов:
2) Уравнение прямой в пространстве, проходящей через две точки.
Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) и M2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
Кроме того, для точки М1 можно записать:
Решая совместно эти уравнения, получим:
Это уравнение прямой, проходящей через две точки в пространстве.
3)Общее уравнения прямой
Если на плоскости введена ПДСК, то всякое уравнение первой степени относительно текущих координат и
где
Верно и обратное утверждение: в ПДСК любая прямая может быть задана уравнением первой степени вида (5).
Уравнение вида (5) называется общим уравнением прямой. Частные случаи уравнения (5) приведены в следующей таблице
Вопрос 20
34. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.
Под углом между плоскостями понимается один из двугранных углов, образованных этими плоскостями.
Угол между нормальными векторами =(A ;B ; C ) и =(A2;B2; C2) плоскостейQ1иQ2 равен углу между этими плоскостями. Поэтому
или
Пример: Заданы две плоскости и(ABM): -4x-5y+5z-12=0.
Для нахождения острого угла следует взять модуль правой части.
Если плоскости перпендикулярны, то их нормальные вектора тоже будут перпендикулярны, т. е.
Если плоскости параллельны, то будут параллельны и их нормали и . Тогда координаты векторов пропорциональны:
Вопрос 22
1)Угол между прямыми: Пересекающиеся прямые l и l1 образуют две пары вертикальных углов. В этом случае углом между прямыми называют один из пары меньших вертикальных углов.
Если прямые скрещиваются (l2 и l3 ), то в углом между прямыми называется угол между пересекающимися прямыми (l2 и m ), который получается в результате параллельного переноса одной из прямых ( l3 ) так, чтобы она пересекала вторую прямую.
В обоих случаях, угол между прямыми равен углу между направляющими векторами этих прямых
Пусть направляющие вектора прямых заданы своими координатами
Тогда для вычисления величины угла между прямыми получаем формулу: