Файл: Двойные углы 3 Sin2X Рассмотрим выражение sin2x представим его аргумент в виде 2xxx и воспользуемся известной формулой синуса суммы аргументов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 131
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2)Условия Если прямые перпендикулярны, то в этом и только в этом случае имеем
Если прямые параллельны, то параллельны их направляющие векторы. Следовательно, координаты этих векторов пропорциональны, т. е.
3)Условие, что лежат в одной плоскости Пусть имеем две прямые:
Отсюда, направляющие вектора этих прямых
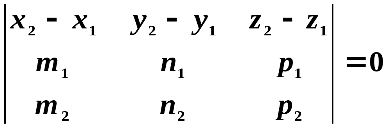 . (32) Условие (32) является также критерием пересечения двух прямых.
. (32) Условие (32) является также критерием пересечения двух прямых.Вопрос 23
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
1)Угол между прямой и плоскостью
Если в пространстве заданы направляющий вектор прямой L s = {l; m; n}
и уравнение плоскости Ax + By + Cz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
2
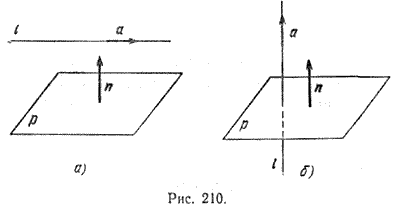 )Условия перпендикулярности и параллельности Прямая с направляющим вектором а и плоскость с нормальным вектором n параллельны тогда и только тогда, когда векторы а и n перпендикулярны. Для перпендикулярности прямой и плоскости, очевидно, необходимо и достаточно, чтобы векторы а и n были коллинеарны (рис. 210, б).
)Условия перпендикулярности и параллельности Прямая с направляющим вектором а и плоскость с нормальным вектором n параллельны тогда и только тогда, когда векторы а и n перпендикулярны. Для перпендикулярности прямой и плоскости, очевидно, необходимо и достаточно, чтобы векторы а и n были коллинеарны (рис. 210, б).Если прямая и плоскость заданы уравнениями
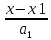 =
=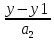 =
=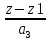 и Ax+By+Cz+D=0
и Ax+By+Cz+D=0 то они: а) параллельны тогда и только тогда, когда а1*А + а2*В + а3*С = 0; (2)
б) перпендикулярны тогда и только тогда, когда a1*A=a2*B=a3* C*d c
a1*A=a2*B=a3*C
3) Прямая:
Плоскость: AX+BY+CZ+D= 0 Очевидно, что координаты точки x1 y1 z1 должны удовлетворять уравнению плоскости:
AX1 + BY1 + CZ1 + D= 0 И условие параллельности прямой и плоскости должно выполняться:
AL + BM + CN= 0 Эти два условия определяют принадлежность прямой к плоскости.
Sinx: x=(−1)n*arcsina+πn, n∈Z
Cosx: x=±arccosa+2πn, n∈Z
Tgx: x=arctga+πn, n∈Z
Ctgx: x=artga+πn, n∈Z