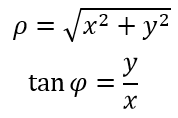Файл: Двойные углы 3 Sin2X Рассмотрим выражение sin2x представим его аргумент в виде 2xxx и воспользуемся известной формулой синуса суммы аргументов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 143
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вопрос 6
1) Операция над двумя векторами, результатом которой является число (когда рассматриваются векторы, числа часто называют скалярами), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними
2) 1) Скалярное произведение двух векторов обладает свойством переместительности:
Доказательство. По определению
Очевидно, что
2) Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию другого вектора на направление первого, то есть
Доказательство. По определению
С другой стороны, по теореме о проекции вектора на ось,
3) Проекция вектора на ось равна скалярному произведению этого вектора на орт рассматриваемой оси, то есть , где - орт оси .
Доказательство. Сформулированное свойство по существу является частным случаем рассмотренного выше свойства 2 и с очевидностью из него вытекает, если принять вектор равным орту
4) Скалярный множитель можно вынести за знак скалярного произведения двух векторов:
.
Доказательство. В силу свойства 2 скалярного произведения двух векторов
Если же, кроме того, принять во внимание свойства сочетательности и переместительности произведения чисел, а также свойство 2 скалярного произведения двух векторов, то получим
5) Скалярное произведение двух векторов обладает свойством распределительности: .
Доказательство. Согласно свойству 2 скалярного произведения двух векторов,
Воспользуемся во втором множителе правой части этого равенства теоремой о проекции суммы векторов на ось. Получим:
Если же снова применить свойство 2 скалярного произведения двух векторов, то придем к выводу, что
6) Имеет место равенство:
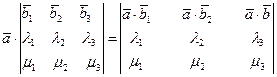
Доказательство. Воспользуемся равенством:
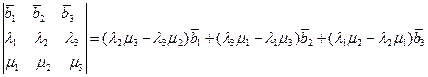
Тогда, в силу свойств 4 и 5 скалярного произведения двух векторов, имеем
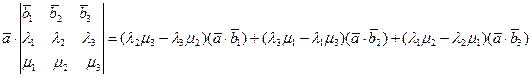 ,
,то есть
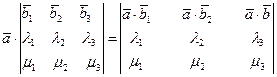
7) Скалярное произведение вектора самого на себя равно квадрату длины этого вектора: .
Доказательство. По определению скалярного произведения двух векторов
откуда с очевидностью следует, что .
8) Теорема 3. Если два вектора определены своими декартовыми прямоугольными координатами а={x1,y1,z1}, b={x2,y2,z2}, то их скалярное произведение равно сумме попарных произведений их соответствующих координат, т.е. a·b=x1x2+y1y2+z1z2 (5)
Доказательство. Т.к. базисные векторы являются попарно ортогональными и имеют единичную длину, то:
Учитывая, что а=x1i+y1j+z1k, b= x2i+y2j+z2k, получим
a·b=(x1i+y1j+z1k)(x2i+y2j+z2k)=x1x2+0+0+y1y2+0+0+z1z2=x1x2+y1y2+z1z2. ч.т.д.
При a=b получаем a·а=|а|2=
Вопрос 7
1) Векторное произведение — это псевдовектор, который перпендикулярен плоскости, построенной по двум сомножителям, которые являются результатом бинарной операции «векторное умножение» над векторами в трехмерном евклидовом пространстве
скалярное произведение векторов угол между векторами коллинеарные векторы компланарные векторы модуль вектора определитель матрицы координаты вектора
2) Векторное произведение равно нулю, если векторы коллинеарны или один из них равен нулю.
3) Пусть заданы два вектора
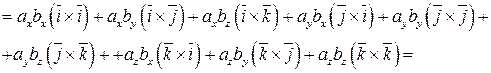
Полученную формулу можно записать еще короче:
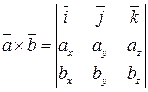 , (9)
, (9)так как правая часть равенства (8) соответствует разложению определителя третьего порядка по элементам первой строки. Равенство (9) легко запоминается.
Вопрос 8
1)Геометрический смысл смешанного произведения.
Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами: Vпарал = |a · [b × c]|
2) Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.
3)Свойства: 1.Объем параллелепипеда, построенного на векторах
2. Объем четырехугольной пирамиды равен трети модуля смешанного произведения
3. . Объем треугольной пирамиды равен одной шестой модуля смешанного произведения
4. Векторы
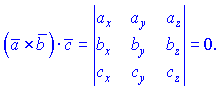
4) а=ахi+ayj+azk, b= bхi+byj+bzk, c= cхi+cyj+czk
abc=(a×b)c=
abc=
Вопрос 9
1)Связь полярных координат с прямоугольными через уравнения