Добавлен: 25.10.2023
Просмотров: 179
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Составим уравнение Лагранжа 2-го рода. В качестве обобщенной координаты примем перемещение груза 1- S. Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид:
где Т- кинетическая энергия системы, Q- обобщенная сил, S- обобщенная координата.
Выражение для кинетической энергии было найдено (1.6)
Для определения обобщенной силы сообщим системе возможное перемещение, при котором координата S получит приращение
Такая сумма работ уже вычислялась (4.3):
В тоже время известно, что
Из (5.3) получим выражение для обобщенной силы:
Подставляя кинетическую энергию (5.2) и обобщенную силу (5.4) в уравнение Лагранжа получаем
Или
6. Результаты вычислений.
с=2000 Н/м
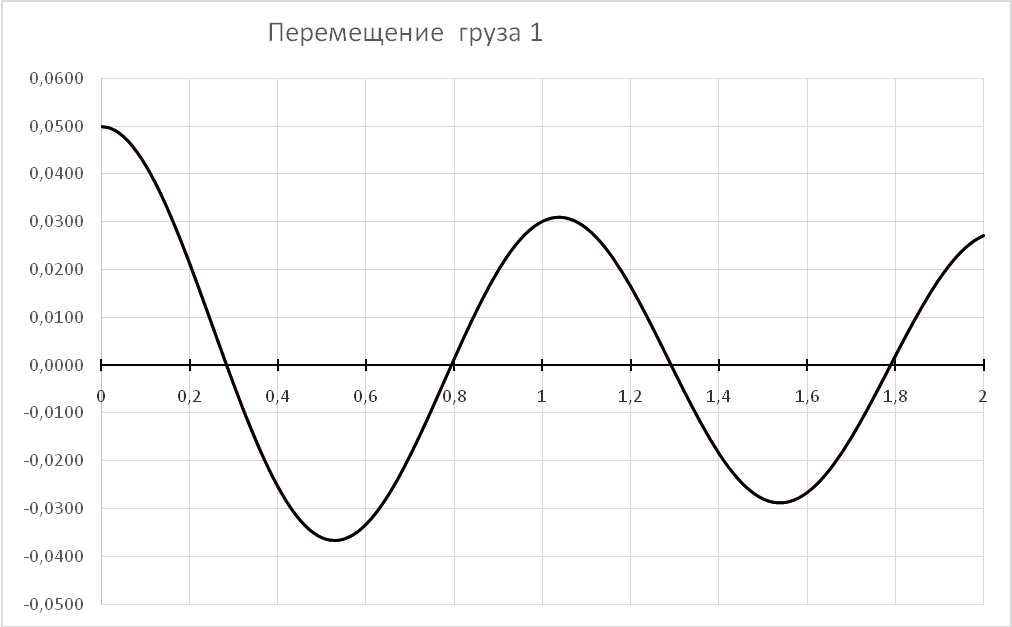
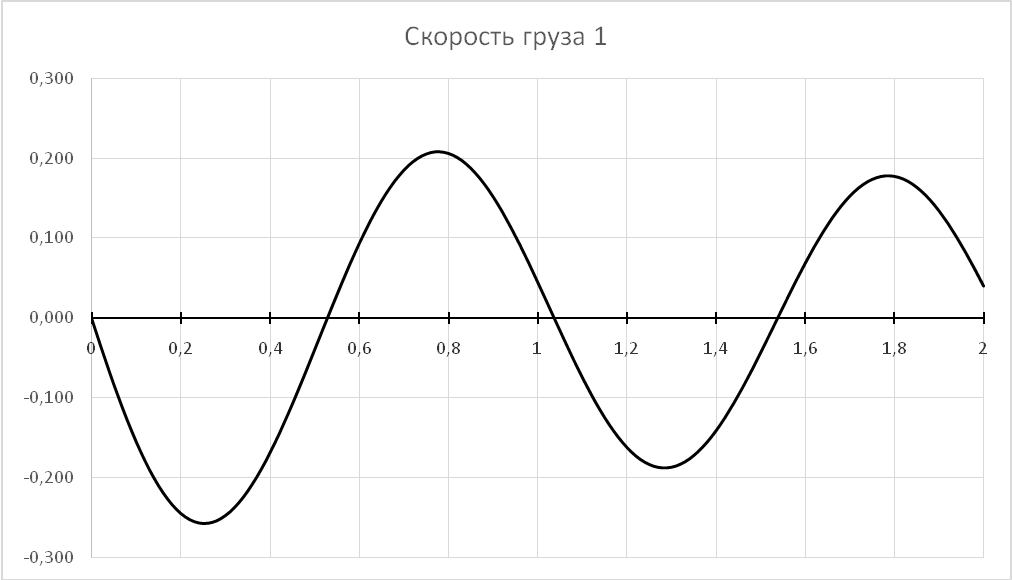
7. Исследование и оптимизация механической системы
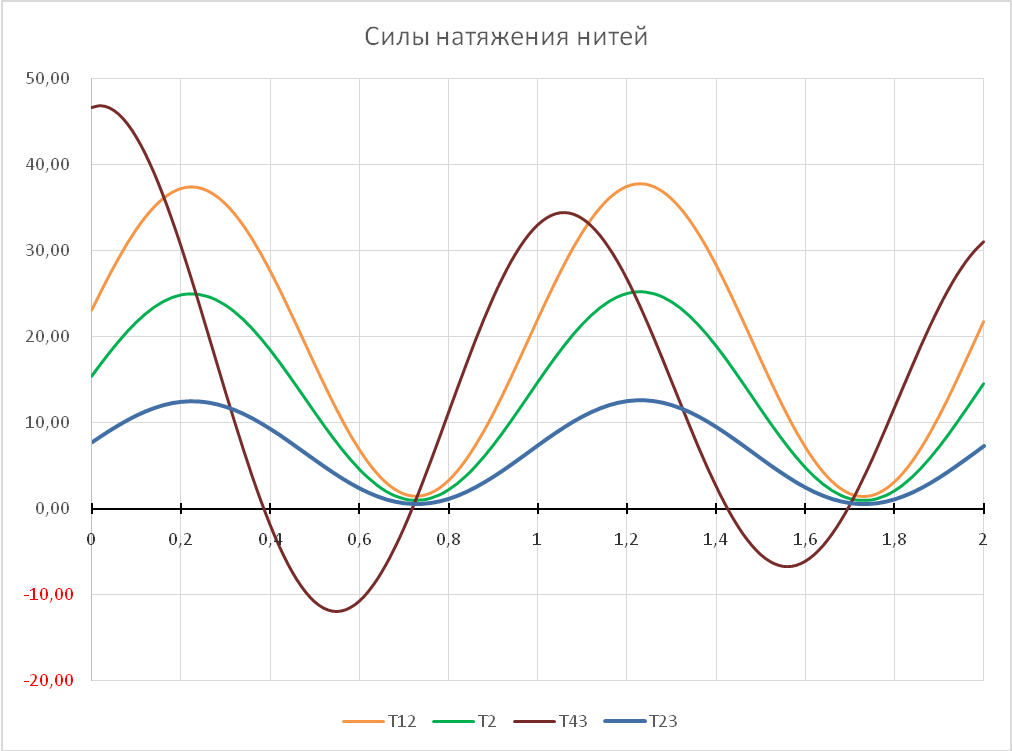
В результате решения дифференциального уравнения были получены законы движения первого груза, его скорость и ускорение в зависимости от времени t. На основании этих зависимостей могут быть определены законы изменения всех остальных характеристик механической системы, в том числе и реакций связей. Поскольку значения параметров системы задавались произвольно, то может возникнуть ситуация, когда натяжение одной из нитей или всех нитей станет отрицательным. В этом случае математическая модель перестает адекватно отражать динамику механической системы. Актуальной становится задача оптимизации параметров механической системы таким образом, чтобы на всем этапе функционирования системы она сохраняла бы свою работоспособность.
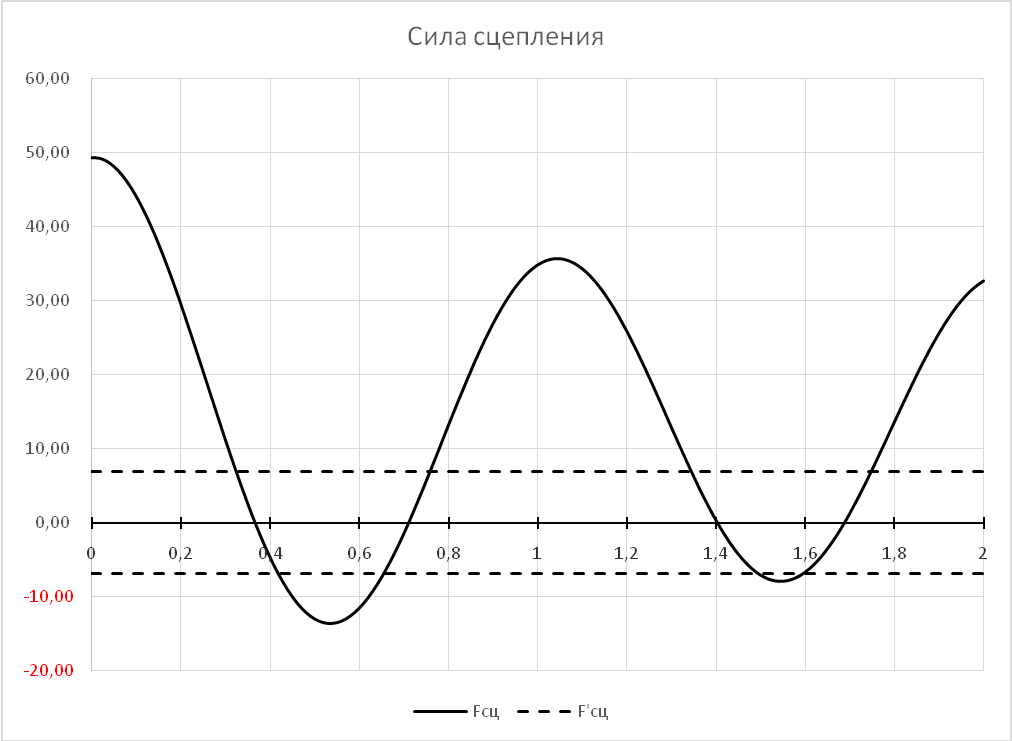
Математическая модель, описывающая поведение исследуемой механической системы, построена в предположении, что каток 4 движется без проскальзывания. Данное утверждение предполагает, что модуль силы сцепления FСЦ подчинен следующему ограничению:
Результаты расчетов показывают, что сила сцепления
Следовательно, математическая модель не соответствует реальному поведению механической системы: каток катится с проскальзыванием, трос, соединяющий тела 3 и 4 в некоторые моменты времени, провисает.
Увеличение массы тела 1 до 3кг устраняет провисание тросов:
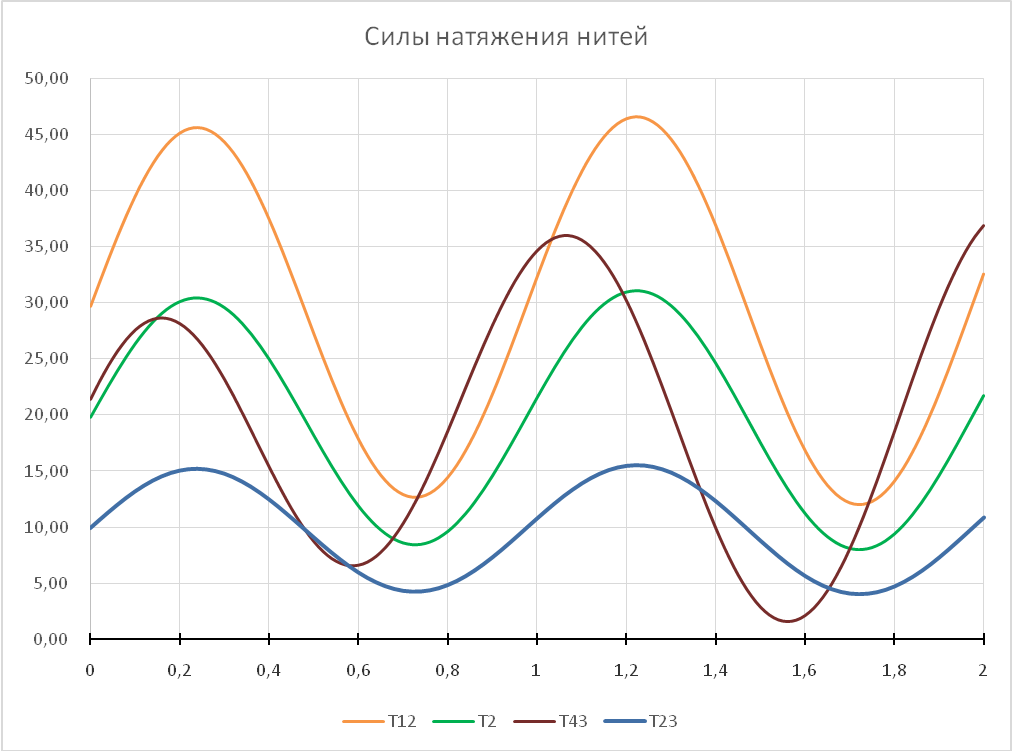
Но проскальзывание катка 4 остается:
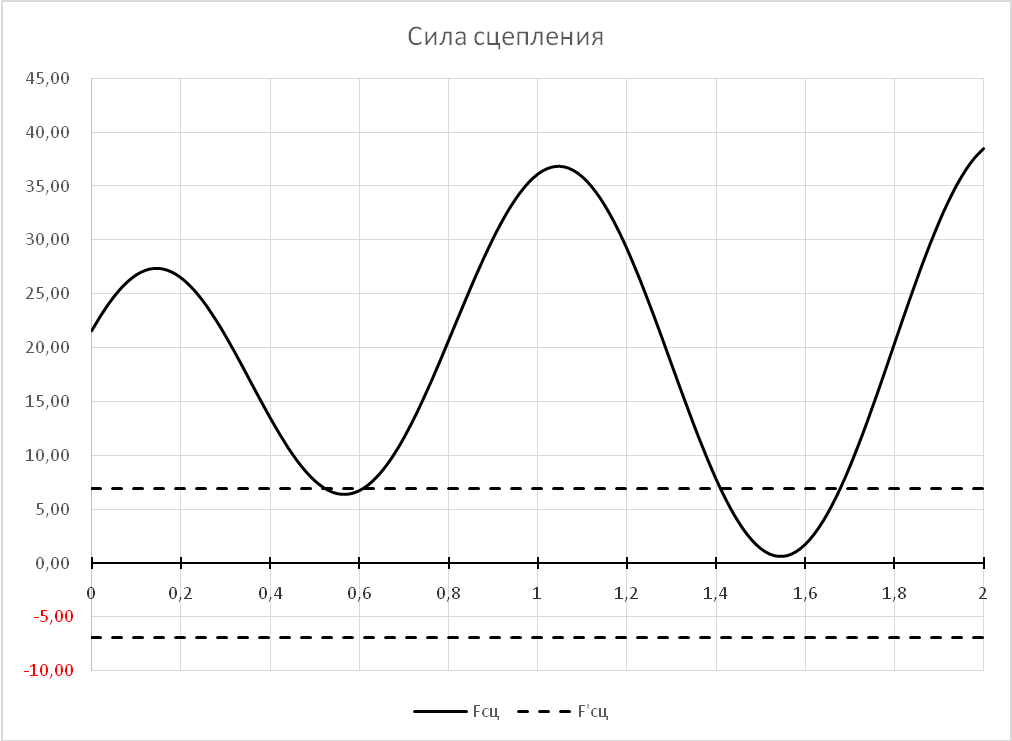
Как показывают расчеты последовательное увеличение массы катка 4 до 22кг и уменьшение жесткости упругого элемента до 1000 Н/м устраняет проскальзывание катка.
Проведем окончательный расчет при следующих параметрах:
с=1000 Н/м
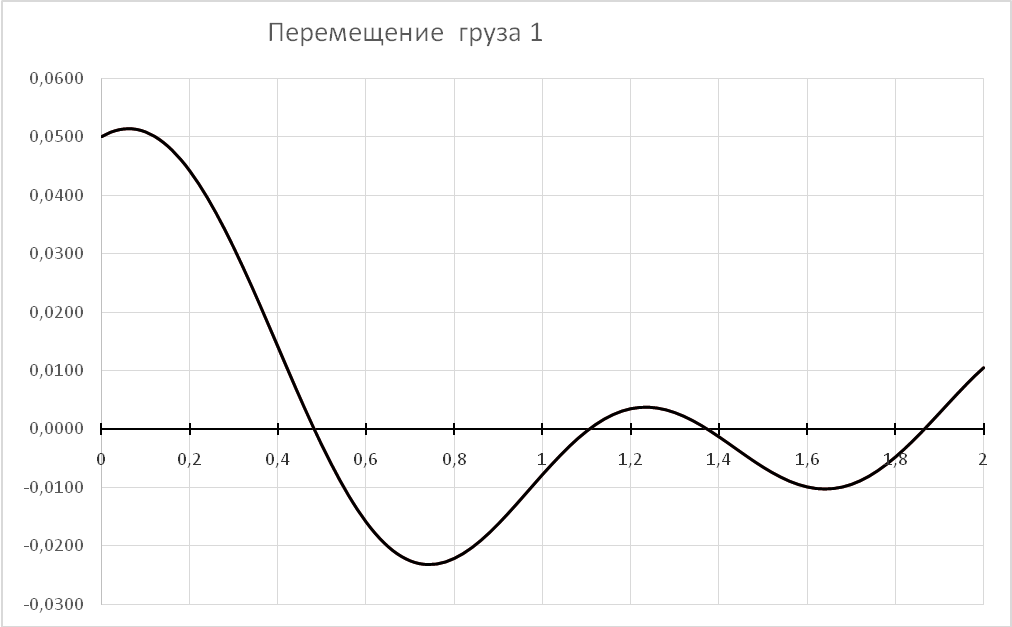
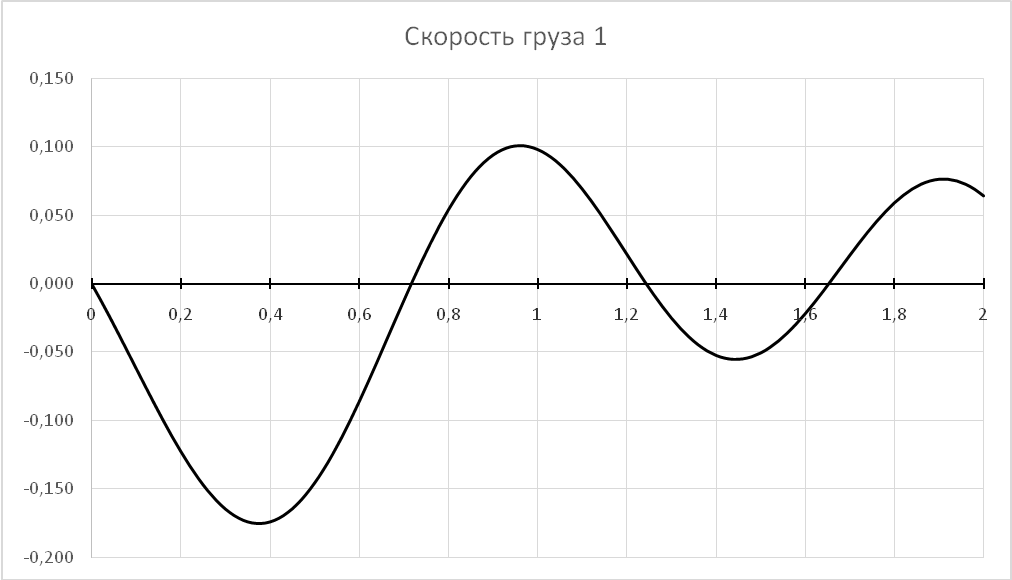
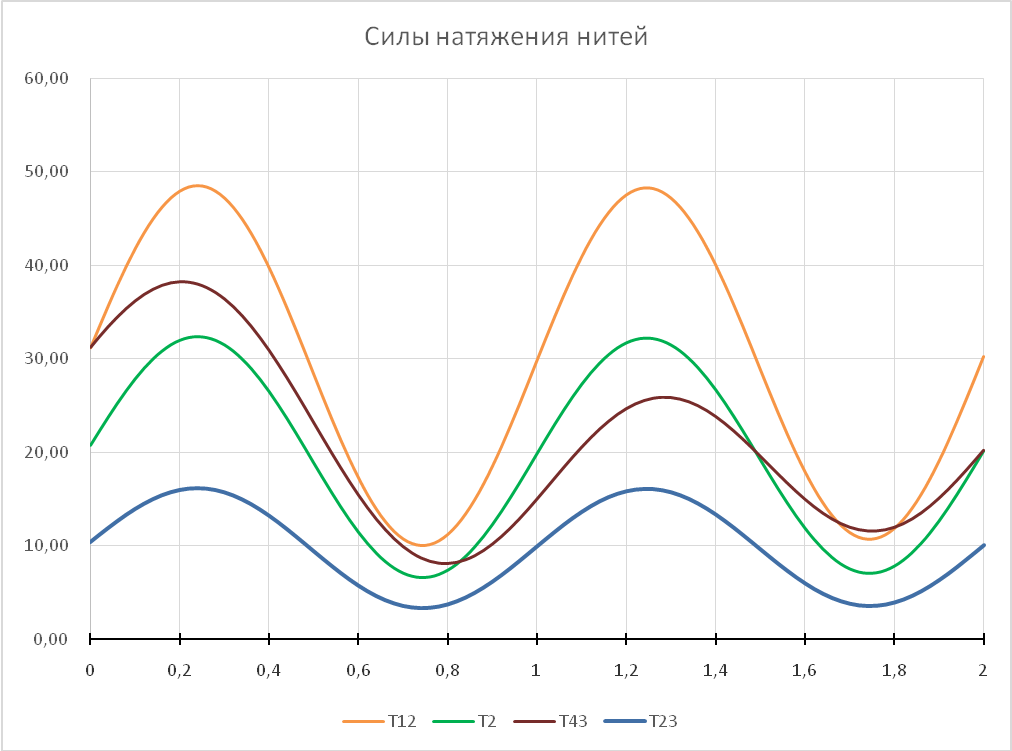
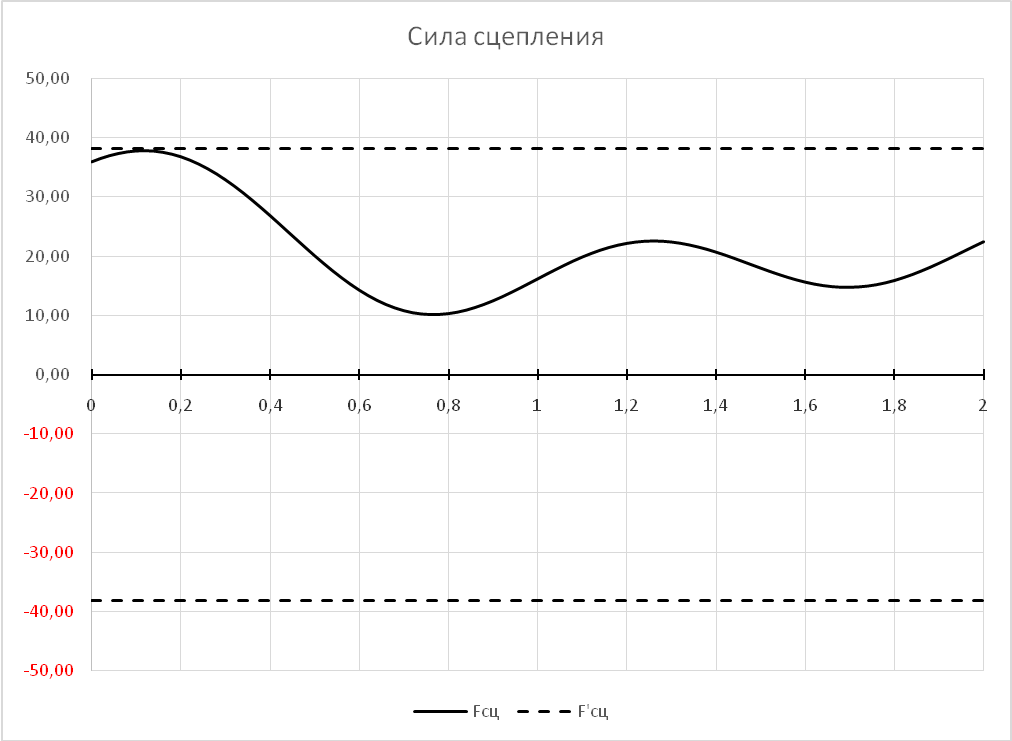
ВЫВОДЫ
При выполнении данной курсовой работы мы приобрели навыки исследования и анализа динамического поведения механической системы с упругими связями, формулировки задач, а также построения расчетной схемы и математической модели. Используя основные теоремы динамики системы и аналитические методы теоретической механики, мы определили закон движения первого тела и реакции внешних и внутренних связей. То, что при использовании различных теорем мы получили одинаковые законы движения, свидетельствует о правильности полученных результатов.
Используя полученный алгоритм расчетов, нашли значение масс груза 1, катка 4, жесткость упругого элемента, при котором выполняются необходимые условия выбранной математической модели. Результаты расчетов скорректированной механической системы представлены в виде графиков, иллюстрирующих изменение интересующих параметров в зависимости от времени.
СПИСОК ЛИТЕРАТУРЫ
1. Бертяев В.Д., Латышев И.И., Маркелов С.С. Расчет плоских и пространственных конструкций: Учеб. пособие. – Тула: ТулГУ, 2011. – 79 с.
2. Бертяев В.Д. Теоретическая механика на базе Mathcad. Практикум. – СПб.: БХВ-Петербург, 2005. – 752 с.
3. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т.1. – М.: Наука, 1979. – 272 с.
4. Тарг С.М. Краткий курс теоретической механики. – М.: Высш. шк., 2005. – 416 с.
5. Яблонский А.А., Никифорова В.М. Курс теоретической механики: Статика. Кинематика. Динамика. – М.: Интеграл-Пресс, 2006. – 608 с.