Файл: Исследование движения механической системы.doc

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное

учреждение высшего образования

«Тульский государственный университет»
Интернет-институт ТулГУ


КУРСОВАЯ РАБОТА

по дисциплине

«Теоретическая механика»

на тему

«Исследование движения механической системы»
Вариант рисунка №3 (номер зачетки 213623)

Вариант исходных данных №1 (год поступления 2021)


Выполнил:

студент группы ИБ161211 Близнин Артем Андреевич

Проверил: Ткач Ольга Александровна
Тула 2023

Оглавление

АННОТАЦИЯ

Исследуется движение механической системы с одной степенью свободы, на которую действуют момент сопротивления и возмущающая гармоническая сила F(t). Трением качения и скольжения пренебрегаем. Качение катков происходит без скольжения, проскальзывание нитей на блоках отсутствует. Требуется, используя основные теоремы динамики системы и аналитические методы теоретической механики, определить закон движения первого тела и реакции внешних и внутренних связей.

Схема механизма и данные для выполнения задания

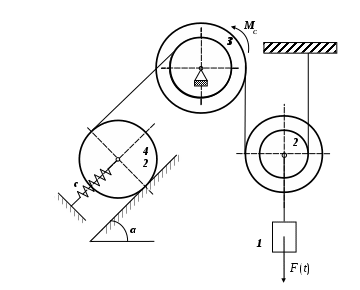
Рис. 1 Схема механизма

---

Исходные данные:

m₁=2m, m₃=3m, m₄=4m — массы тел механической системы,

с =2000Н/м— жесткость упругого элемента,

=0,5 Н м с — коэффициент вязкого трения в подшипнике,

r₂=1,5r, R₂=3r, r₃=r, R₃=2r — радиусы блоков 2, 3

i₂=r*,i₃=2r, i₄=r*, — радиусы инерции,

r₄=2r — радиус блока 4,

m=1кг α=45⁰



- начальные условия.

r* — сплошной однородный цилиндр радиуса "rk",

1. Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы.

Изобразим расчетную схему (рис.2)



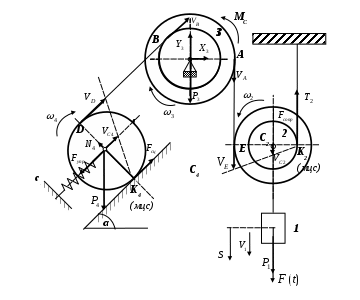
Рис. 2 Расчетная схема

На рис. 2 обозначено:

- силы тяжести,

- нормальная реакция опорной плоскости,

- сила сцепления цилиндра 4 с наклонной плоскостью,

- упругая реакция пружины,

- реакции подшипника блока 3,

- момент сопротивления

- натяжение вертикальной нити, по которой катится цилиндр 2,

- возмущающая сила.

Рассматриваемая механическая система имеет одну степень свободы. Будем определять положение системы с помощью координаты

---

S. Начало отсчета координат совместим с положением статического равновесия груза 1.

Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:

(1.1)

Где Т- кинетическая энергия системы,

- сумма мощностей внешних сил,

- сумма мощностей внутренних сил.

Вычисляем кинетическую энергию системы.

Кинетическая энергия системы определяется суммой кинетических энергий тел:

Т= Т₁+ Т₃+Т₄ (1.2)

Где , ,

Момент инерции катка: (1.3)

Момент инерции блока: (1.4)

Так как система имеет одну степень свободы и в качестве координаты, определяющей ее положение, принято перемещение груза 1, то кинематические характеристики всех тел механизма выражаем через кинематические характеристики груза 1 соотношениями:

, ,



, (1.5)







Записываем выражение для кинетической энергии системы:

---

Подставляем в (1.2) все скорости, выраженные через (1.5) и моменты инерции тел (1.3),(1.4):



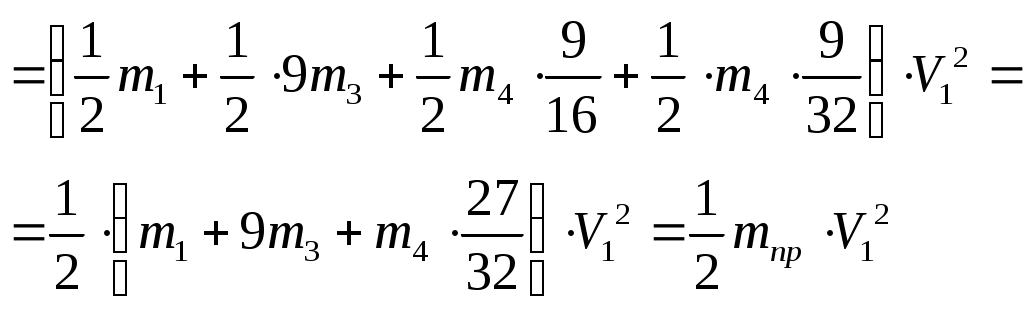(1.6)

где

(1.7)

-приведенная масса системы.

Вычисляем правую часть уравнения (1.1) - сумму мощностей внешних и внутренних сил.

Рассматриваемая нами механическая система является неизменяемой, т. е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому мощности внутренних сил будут равняться нулю .

Будут равняться нулю и мощности внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы , , , , , , .

Мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения.

Сумма мощностей остальных сил равна:



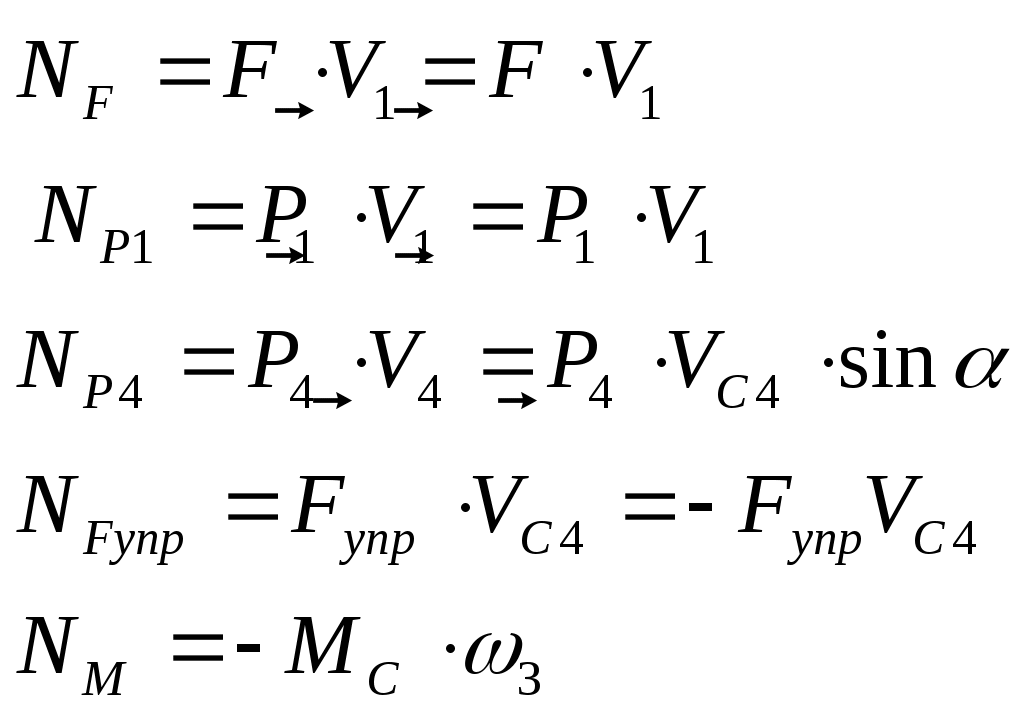
Или

С учетом кинематических соотношений (1.5) сумму мощностей внешних сил преобразуем к виду:

(1.8)

где (1.9)

- приведенная сила.

Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины равно суме статического

---

и динамического удлинений .

Так как , то и упругая сила будет равна: .

Так как , то момент вязкого сопротивления

.

Тогда приведенная сила (1.9) в развернутой форме будет определяться выражением:

(1.10)

В состоянии покоя и условием равновесия системы определяется уравнением



Так как , то

(1.11)

Из уравнения (1.11) определяем статическое удлинение пружины

(1.12)

Окончательное выражение для приведенной силы будет иметь вид:

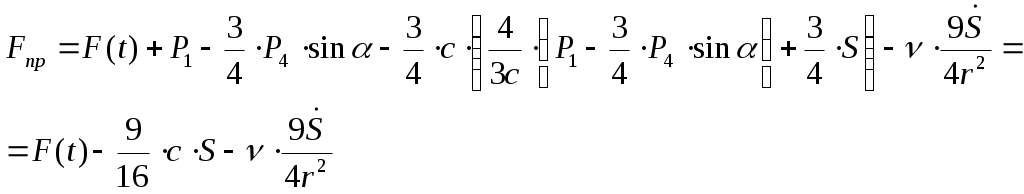(1.13)

Подставим выражение для кинетической энергии (1.6) и сумму мощностей всех сил (1.8) с учетом (1.13) в уравнение (1.1). Тогда, после дифференцирования, получим дифференциальное уравнение движения системы:



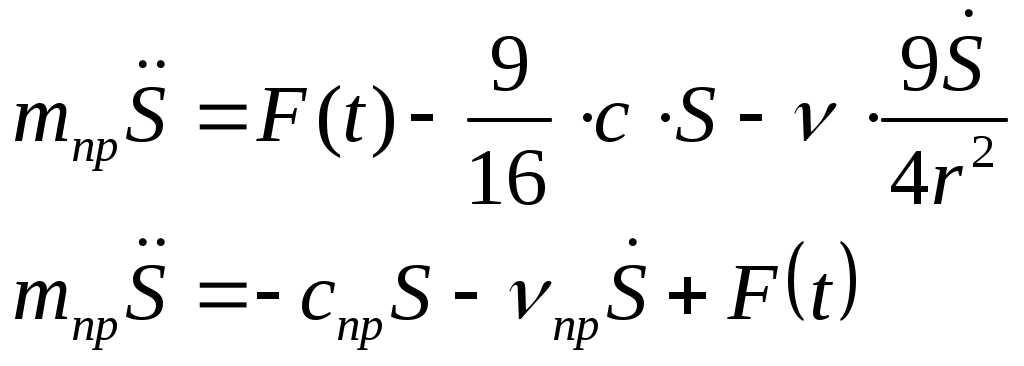
Обозначив - приведенная жесткость пружины

- приведенный коэффициент сопротивления

Получим

---