Добавлен: 25.10.2023
Просмотров: 171
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Представим полученное уравнение в виде:
где введены коэффициенты:
Начальные условия:
при
Уравнения (1.15) и (1.14) представляют математическую модель для решения второй задачи динамики.
2. Определение закона движения системы.
Возмущающая сила изменяется по гармоническому закону:
где
Дифференциальное уравнение движения механической системы с учетом выражения для возмущающей силы примет вид:
где
Общее решение однородного дифференциального уравнения (2.1) складывается из общего решения однородного уравнения и частного решения неоднородного. Однородное дифференциальное уравнение, соответствует неоднородному уравнению (2.1), имеет вид:
Решение этого уравнения ищем виде функции
где
Подставляем (2.3) в (2.2), получим:
Так как мы ищем нетривиальное решение, то
Следовательно, должно выполнятся условие:
Уравнение (2.4) называется характеристическим уравнением дифференциального уравнения (2.2). Это уравнение имеет 2 корня:
(2.5)
где
В этом случае (n<k) общее решение уравнения (2.2) имеет вид:
где
Определим частное решение неоднородного дифференциального уравнения (2.1). Частное решение ищем в виде правой части
Где
Подставляем (2.7) в (2.1) и преобразовываем:
Сравнивая коэффициенты при соответствующих тригонометрических функциях, справа и слева, получим систему алгебраических уравнений для определения постоянных
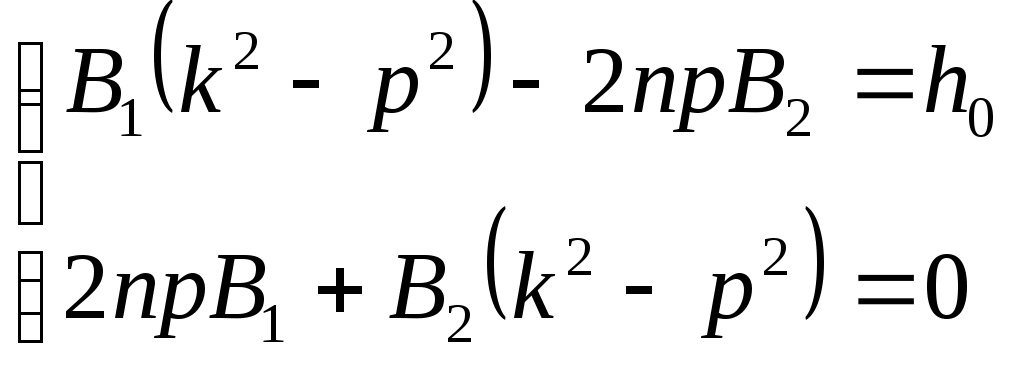
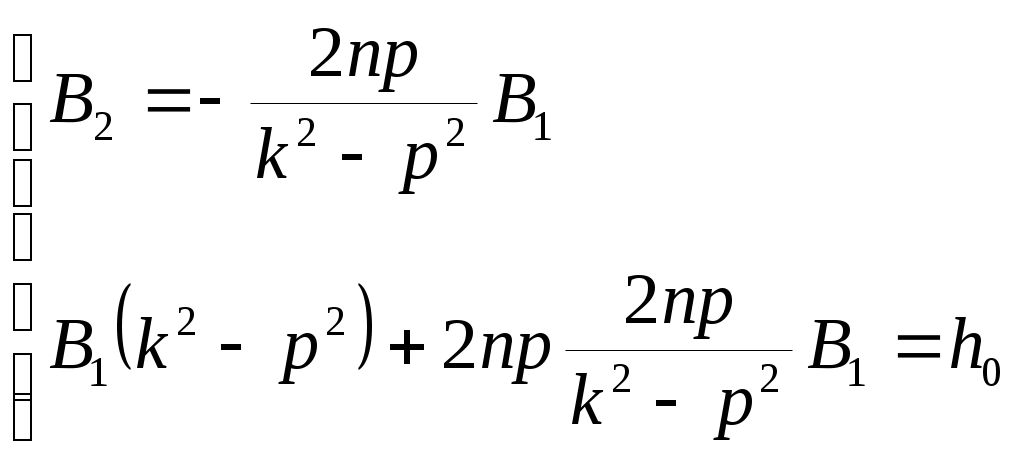
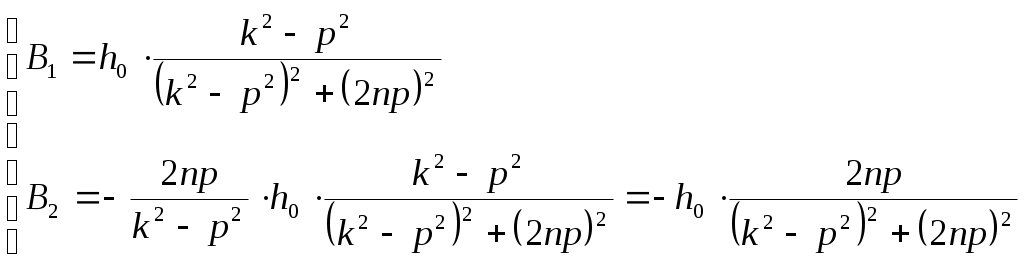
В результате получим:
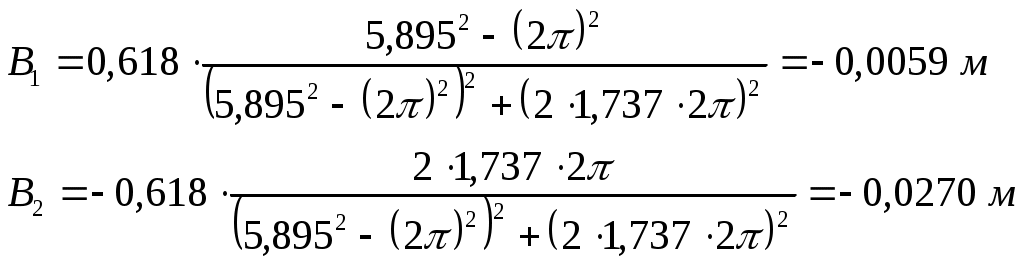
И
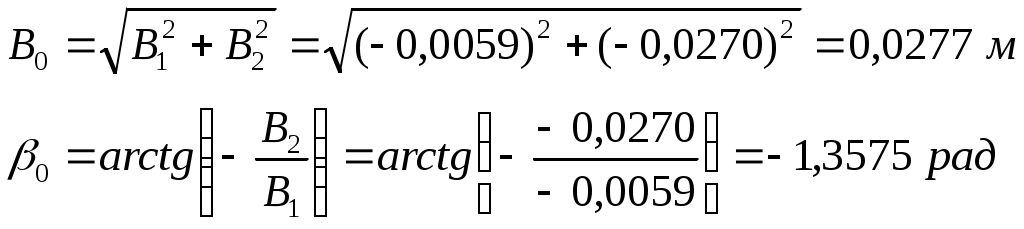
Таким образом, решение (2.7) найдено.
Складывая (2.7) и (2.6), получаем общее решение неоднородного уравнения (2.1).
Постоянные
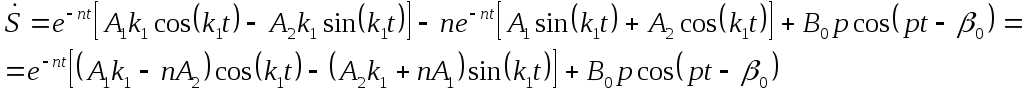 (2.9)
(2.9)В результате получим систему уравнений:
Решаем данную систему:
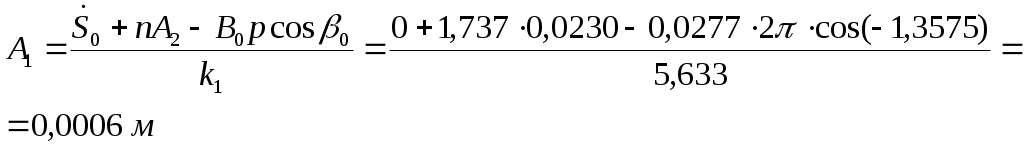
И
И подставляя (2.10),(2.11) в (2.8), получаем закон движения механизма, выраженный через перемещение груза:
3. Определение реакций внешних и внутренних связей.
Для решения этой задачи расчленяем механизм на отдельные части и рисуем расчетные схемы отдельно для каждого тела.
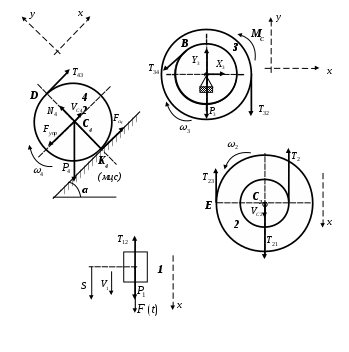
Рис. 3. Расчетные схемы для каждого тела механизма
К каждому телу, изображенному на расчетной схеме, применим две из основных теорем механики материальной системы: теорему об изменении количества движения и теорему об изменении кинетического момента.
Для каждого тела уравнения (3.1) и (3.2) записываем в проекциях на оси координат соответственно схеме рис.3:
Тело1:
Тело 2:
Тело 3:
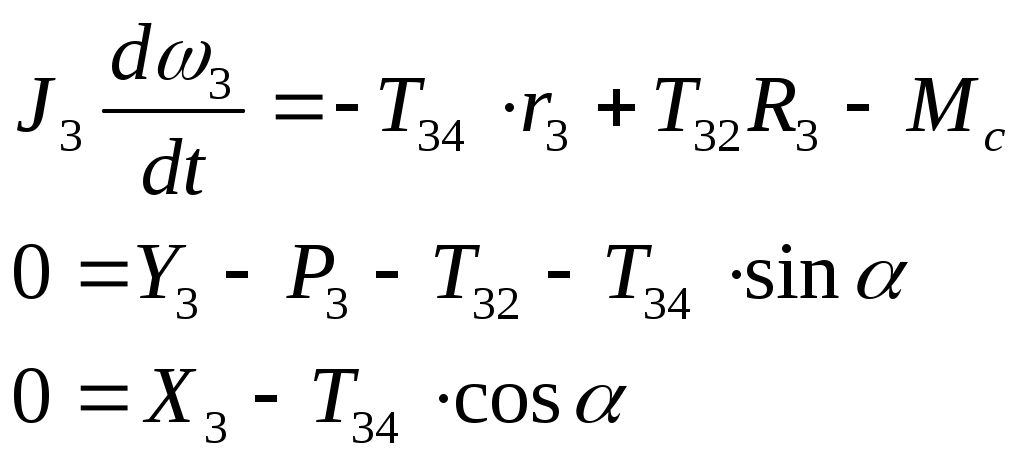 (3.5)
(3.5)Тело 4:
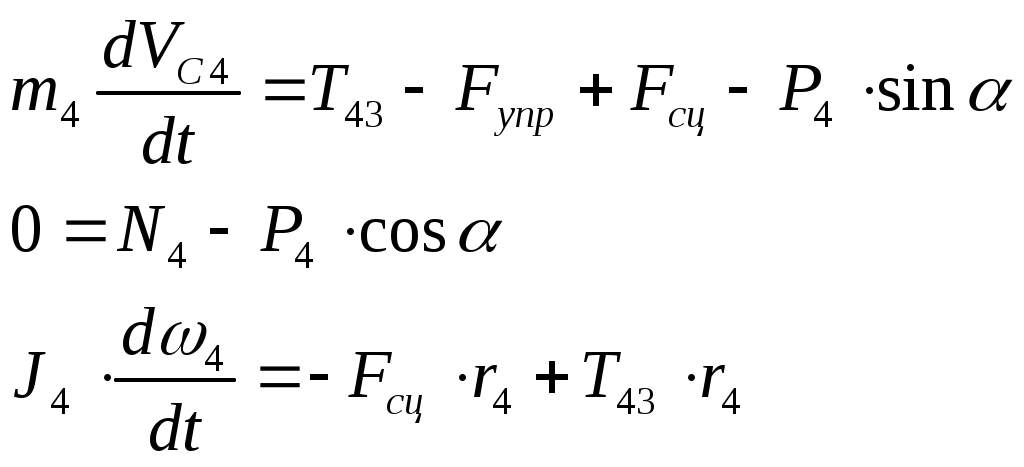 (3.6)
(3.6)С учетом кинематических соотношений (1.5), а также (1.3) и (1.4) систему уравнений преобразуем к виду:
(3.3)
(3.4)
(3.5)
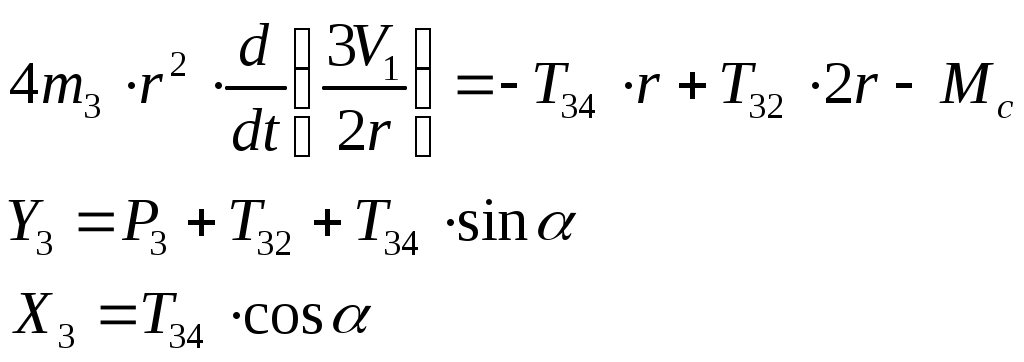
(3.6)
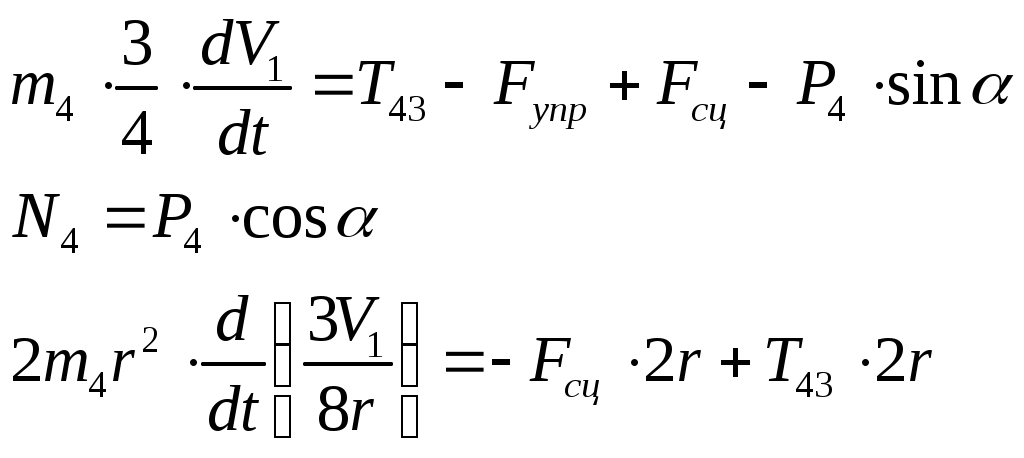
В результате получим:
(3.3)
(3.4)
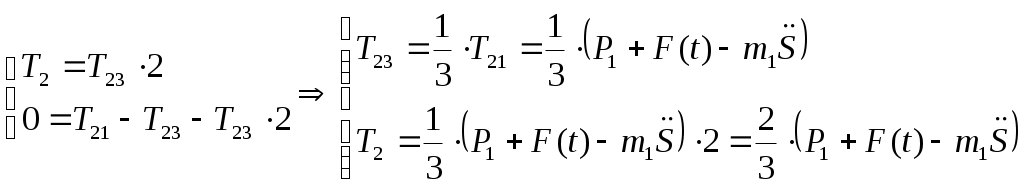
(3.6)
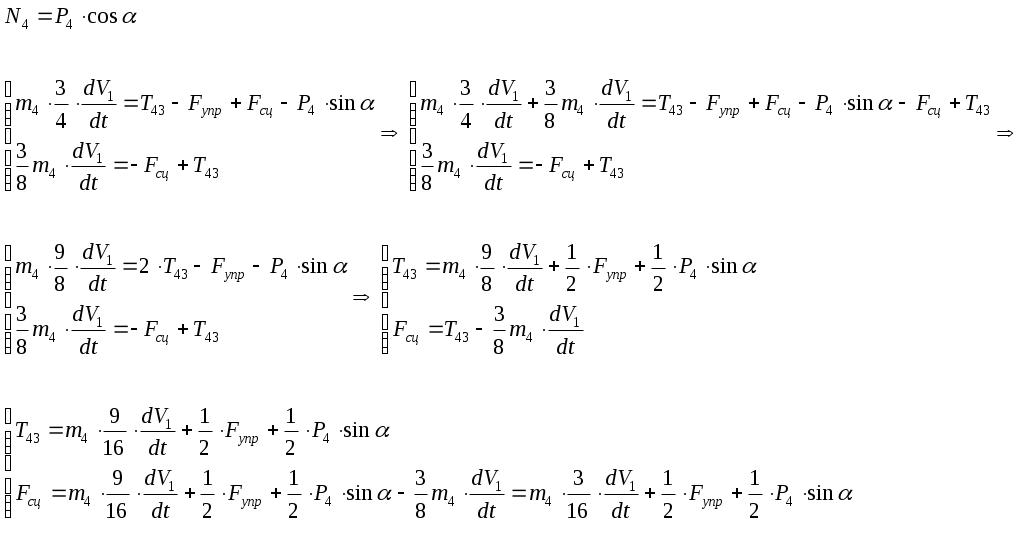
(3.5)
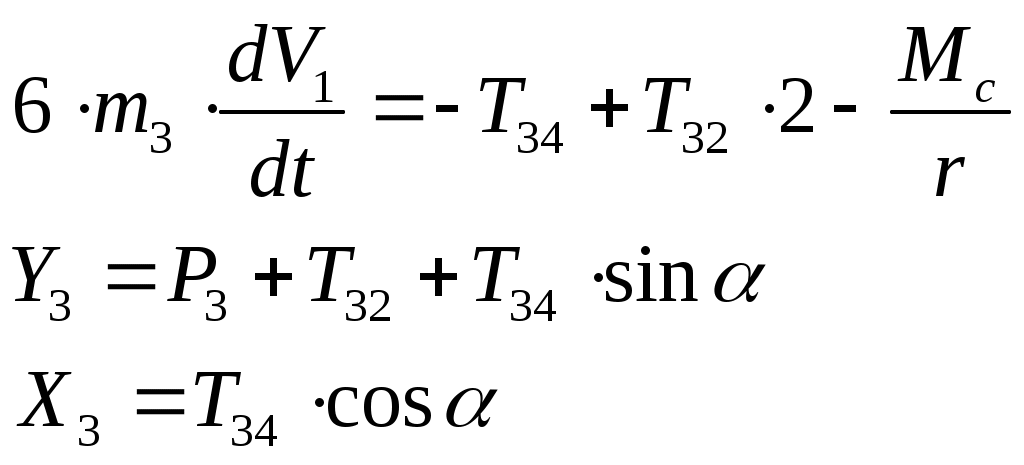 (3.7)
(3.7)Или
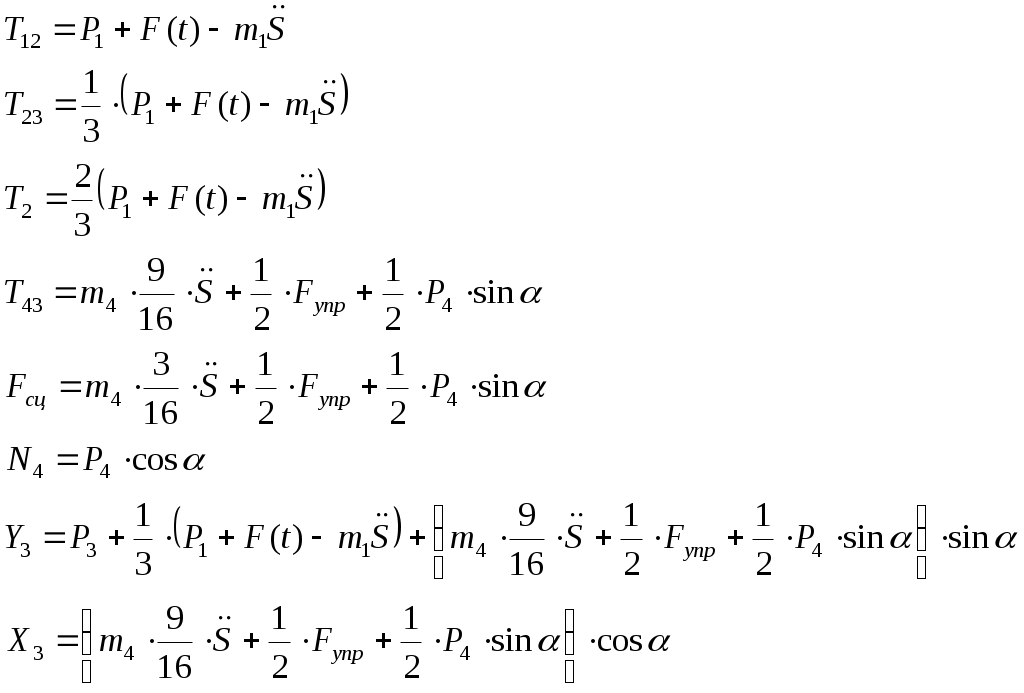 (3.8)
(3.8)Уравнения (3.8) выражают зависимость внутренних и внешних усилий относительно функции
Подставив в первое уравнение системы (3.7), получим уравнение движения системы:
Так как
4. Составление дифференциального уравнения движения механизма с помощью принципа Даламбера.
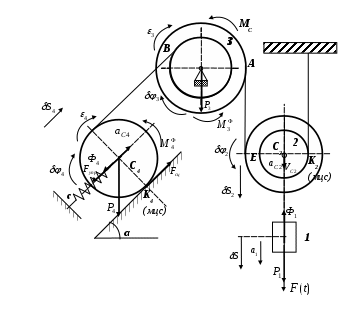
Рис. 4. Расчетная схема
Общее уравнение динамики системы есть математическое выражение принципа Даламбера-Лагранжа
где
На чертеже изобразим все активные силы и силы инерции(рис.4).
Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:
Сумма элементарных работ вычисляется, как и мощность по формуле (1.8) с учетом (1.13)
Определяем возможную работу сил инерции:
Для величин главных векторов и главных моментов сил инерции имеем следующие выражения:
Используя кинематические соотношения (1.5), можно записать:
В результате подстановки с учетом, что
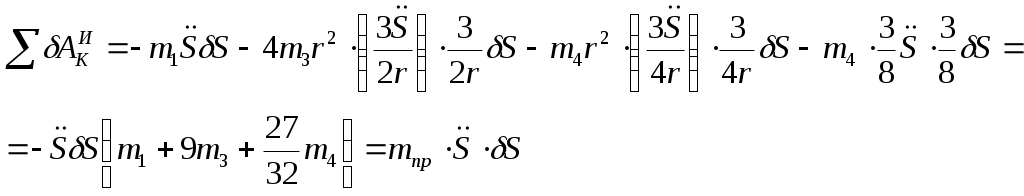 (4.7)
(4.7) Где
Подставляем выражения (4.3) и (4.7) в общее уравнение динамики (4.1) получим:
Разделив (4.9) на
Где
Дифференциальное уравнение (4.9) полностью совпадает с уравнением (1.14) полученным ранее.