ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 620
Скачиваний: 3
СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.2. Температурное поле. Градиент температуры. Тепловой поток
1.4. Дифференциальное уравнение теплопроводности
2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА ПРИ СТАЦИОНАРНОМ РЕЖИМЕ
2.1. Теплопроводность плоской стенки при граничных условиях первого рода
2.2. Теплопроводность цилиндрической стенки при граничных условиях первого рода
2.4. Критический диаметр тепловой изоляции
3. ТЕПЛОПРОВОДНОСТЬ ТЕЛ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛАПРИ СТАЦИОНАРНОМ РЕЖИМЕ
3.1. Теплопроводность однородной пластины
3.2. Теплопроводность однородного цилиндрического стержня
3.3. Теплопроводность цилиндрической стенки
4.1. Теплообмен излучением между твердыми телами, разделенными диатермичной средой
4.2. Особенности излучения газов
5.1. Теплопередача через плоскую стенкусо сложным теплообменом
5.2. Теплопередача через цилиндрическую стенкусо сложным теплообменом
5.3. Интенсификация теплопередачи
6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНАИ ОСНОВЫ ТЕОРИИ ПОДОБИЯИ МОДЕЛИРОВАНИЯ ПРОЦЕССОВ
6.1. Дифференциальные уравнения теплообмена
6.3. Моделирование теплоотдачи
6.4. Физические особенности процесса теплоотдачи
7. ТЕПЛООТДАЧА В ОДНОФАЗНОЙ СРЕДЕ
7.1. Теплоотдача при свободном движении жидкости
7.2. Теплоотдача при продольном омывании поверхности вынужденным потоком жидкости
7.3. Теплоотдача при вынужденном течении жидкости в трубах и каналах
7.4. Теплоотдача при поперечном обтекании труб
8. ТЕПЛООТДАЧА ПРИ ФАЗОВЫХ ПРЕВРАЩЕНИЯХ
8.2. Теплоотдача при конденсации
9.1. Классификация теплообменников
Зная закон изменения температурного напора вдоль поверхности теплообмена (9.12), можно найти средний температурный напор
| | (9.15) |
Совместное решение (9.15), (9.12) – (9.14) дает расчетную формулу для среднего температурного напора при прямотоке
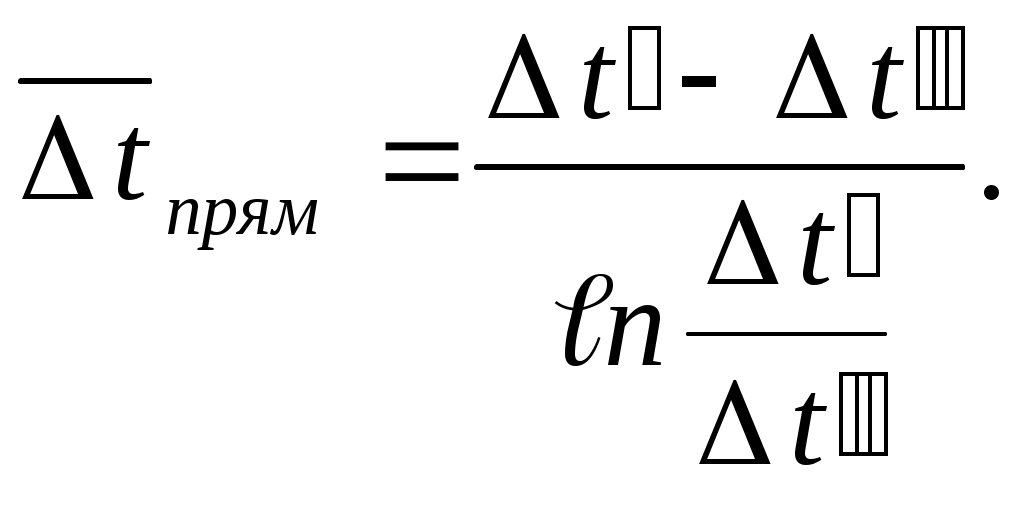 | (9.16) |
При противотоке
| |
Аналогичные рассуждения и математические преобразования дают расчетную формулу для
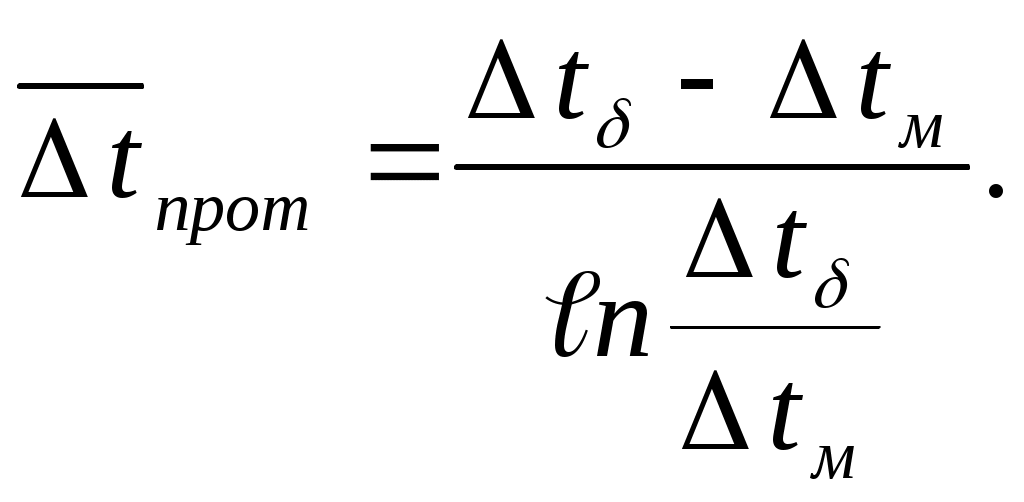 | (9.17) |
Учитывая, что для прямотока Δt является бóльшим температурным напором, а Δt - меньшим, можно утверждать, что формула (9.17) справедлива и для прямотока.
Для других схем движения теплоносителей средний температурный напор рассчитывается по формуле
| | (9.18) |
где t=f (R, P) – поправочный коэффициент, определяемый по номограммам, которые приведены в справочниках.
Здесь
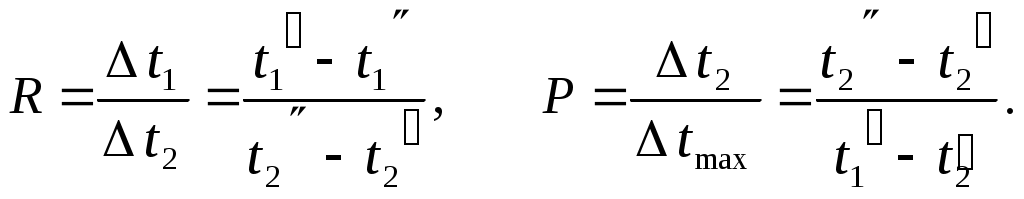 |
Расчет средних температур теплоносителей
= t2-t2; среднюю температуру теплоносителя с меньшим изменением температуры (с бóльшей расходной теплоемкостью) вычисляют как среднюю арифметическую. Среднюю температуру другого теплоносителя определяют по формуле (9.6).
Уравнение массового расхода теплоносителя имеет вид
| G=w f , кг/с, | (9.19) |
где w, м/с – скорость движения теплоносителя,
f, м2 – площадь поперечного сечения потока теплоносителя,
, кг/м3 – плотность теплоносителя.
При движении теплоносителя по трубам пучка площадь поперечного сечения всех труб
| |
где п – число труб.
9.3. Расчет теплообменников
Конструкторский расчет теплообменников производится по уравнениям теплопередачи, теплового баланса, массового расхода теплоносителей.
Получим уравнения для поверочного расчета, цель которого – определить передаваемую теплоту (Q) и конечные температуры теплоносителей (t1, t2).
Прямоток
На основании (9.14)
| | |
или
| | (9.20) |
Если левую и правую части уравнения (9.20) вычесть из разности температур (t1- t2) и учесть соотношение (9.4), то получим формулу (9.21), из которой можно найти температуру горячего теплоносителя (t1) на выходе из теплообменника,
| | (9.21) |
где
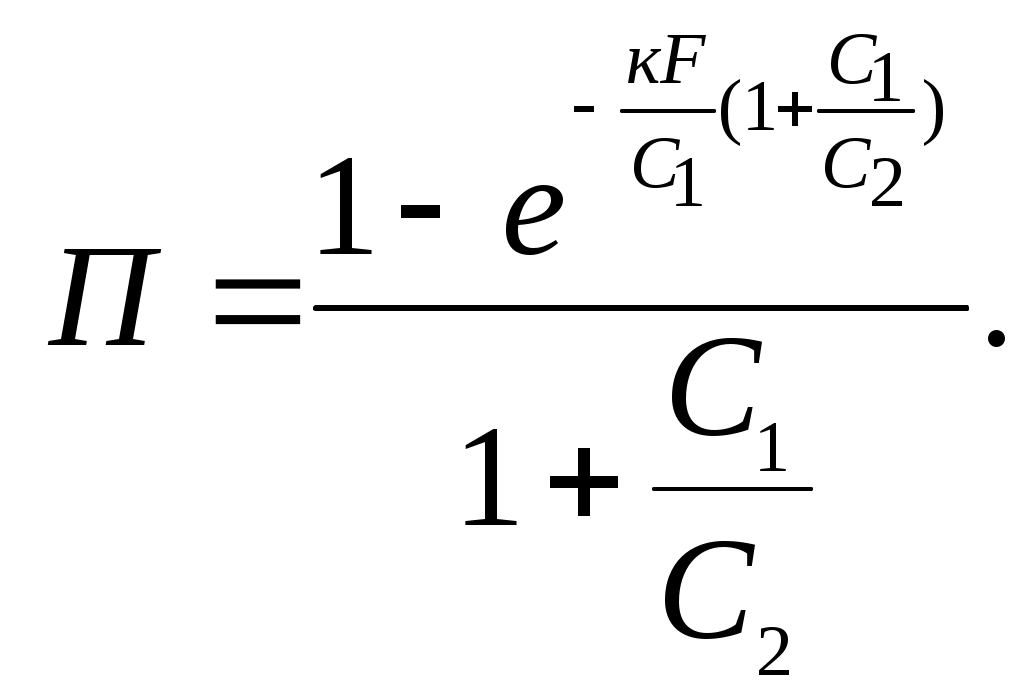 |
Тогда передаваемая теплота и температура холодного теплоносителя (t2) определяется из уравнения теплового баланса
| | (9.22) |
| | (9.23) |
Противоток
Аналогичные алгебраические преобразования для противотока дают расчетную формулу для тепла
| | (9.24) |
где
 |
Конечные температуры теплоносителей (t1, t2) можно рассчитать по уравнению теплового баланса (9.3).
П
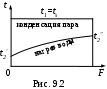 олучим уравнения для поверочного расчета теплообменников с кипением и конденсацией.
олучим уравнения для поверочного расчета теплообменников с кипением и конденсацией.1. Конденсатор, охлаждаемый водой. График изменения температур теплоносителей приведен на рис. 9.2.
При конденсации пара
t1=ts=const, t1=0,
Тогда
| |
а на основании (9.20) получим формулу
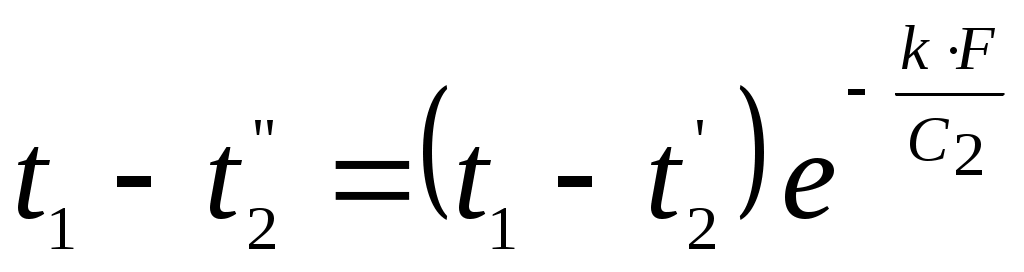 , , |
по которой можно рассчитать конечную температуру холодного теплоносителя
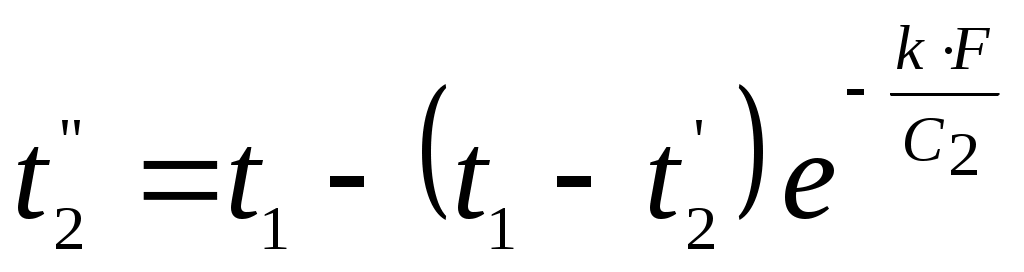 , , | (9.25) |
а затем определить передаваемую теплоту
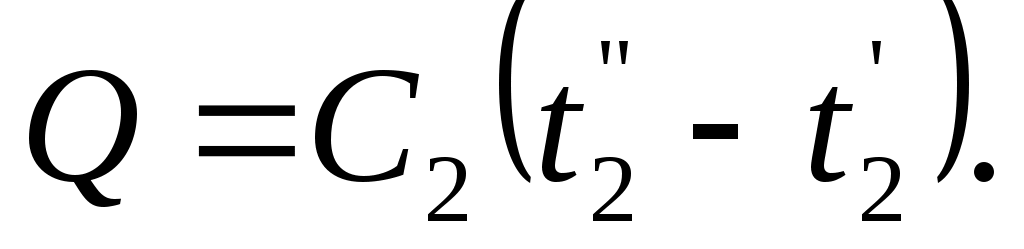 | (9.26) |
2. Испаритель воды, нагреваемый продуктами сгорания топлива, рис. 9.3.
П
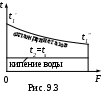 ри кипении воды t2=tS=const, Δt2=0;
ри кипении воды t2=tS=const, Δt2=0; Тогда
на основании (9.20)
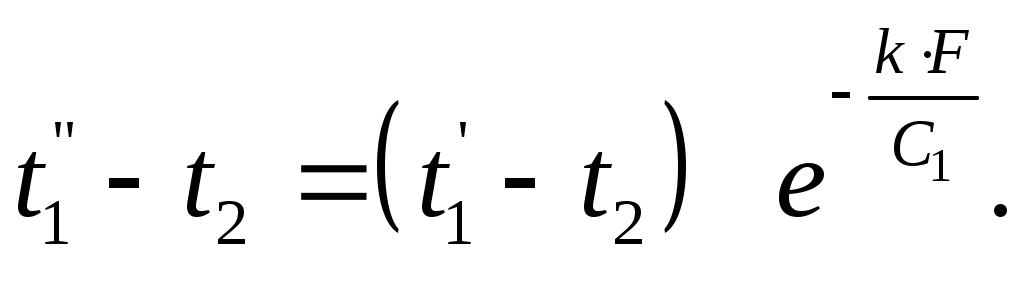 |
Расчетные формулы для
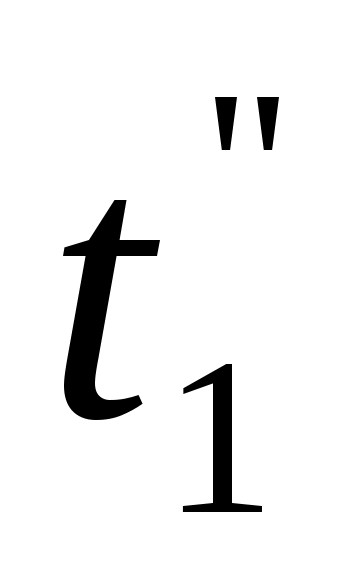 и Q запишутся в виде
и Q запишутся в виде 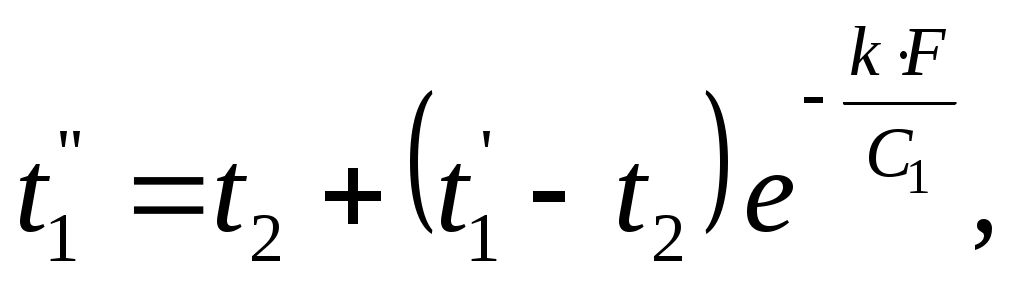 | (9.27) |
| | (9.28) |
Сравнение двух основных схем движения теплоносителей прямотока и противотока можно произвести на основании уравнений (9.22) и (9.24)
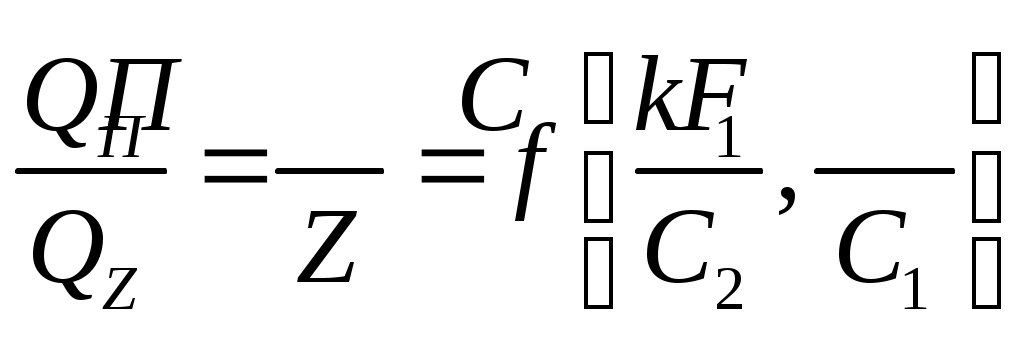 . . | (9.29) |
Анализ зависимости (9.29) показывает, что прямоток и противоток равнозначны при следующих условиях:
-
Если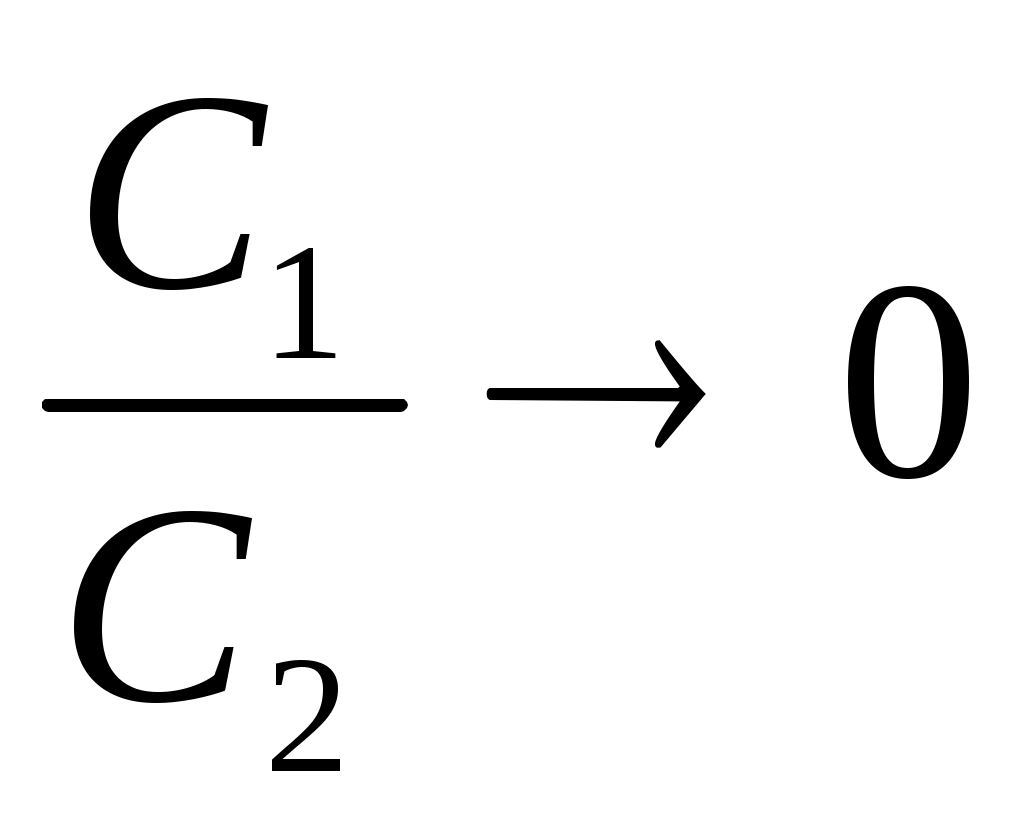 или
или 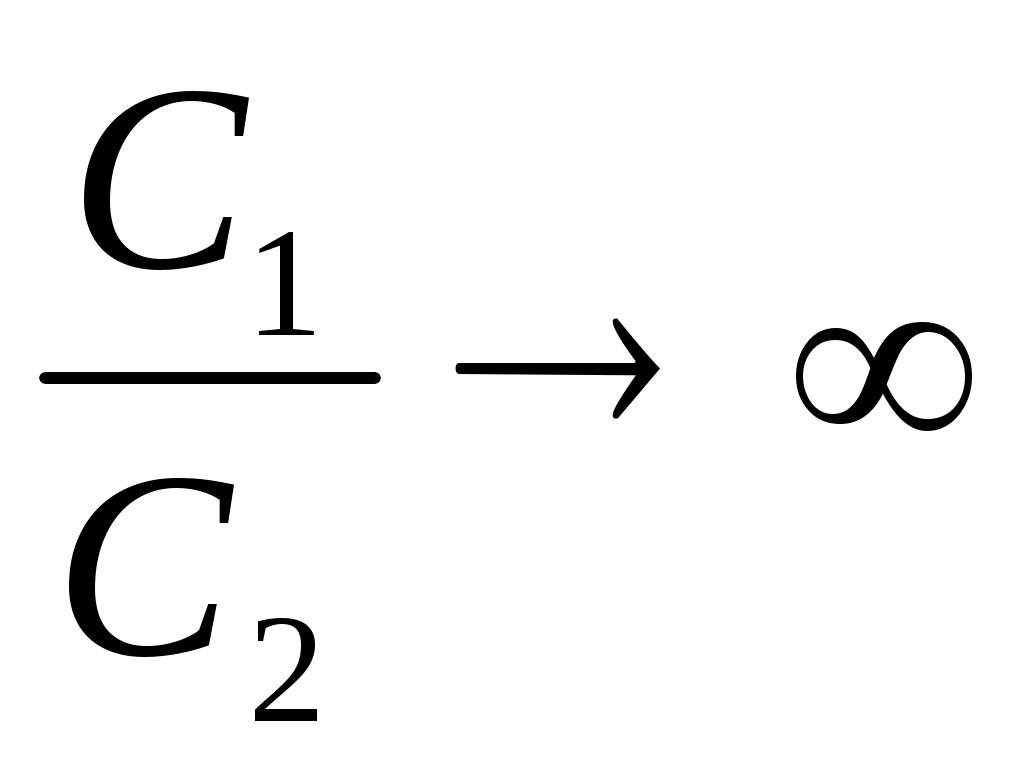 , т.е. для теплообменников, в которых один из теплоносителей изменяет свое агрегатное состояние (испаряется или конденсируется).
, т.е. для теплообменников, в которых один из теплоносителей изменяет свое агрегатное состояние (испаряется или конденсируется). -
Если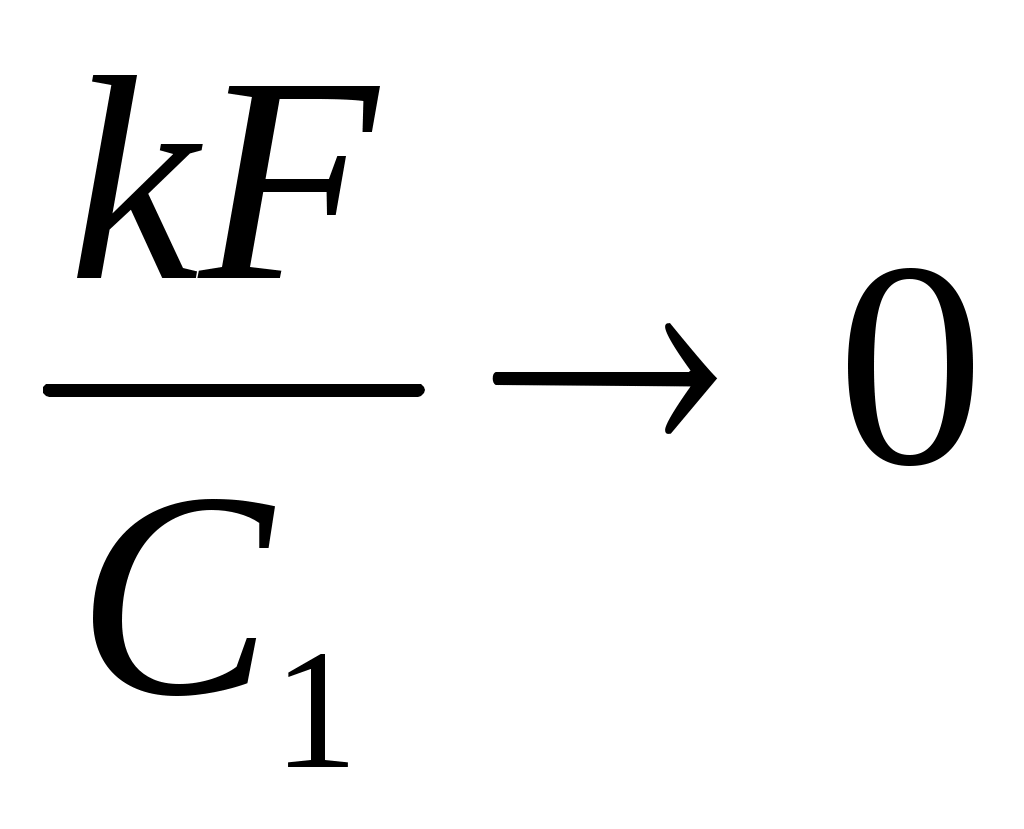 , что справедливо при
, что справедливо при 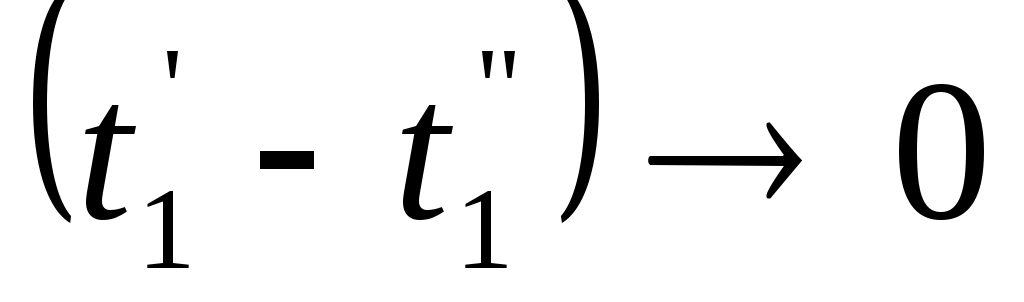 или
или 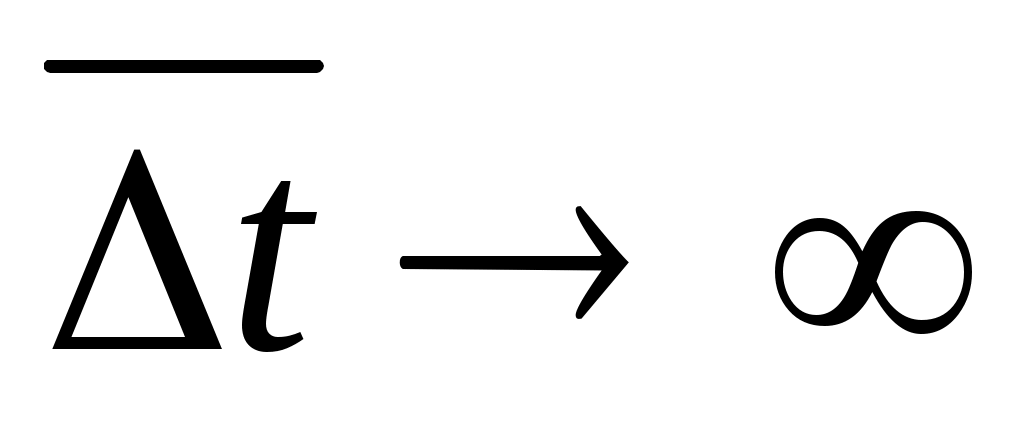 .
.
Во всех остальных случаях
Контрольные вопросы и задания
1. Назовите основные уравнения для расчета рекуперативных теплообменников. Какими коэффициентами оценивается эффективность работы теплообменников?
2. Можно ли утверждать, что КПД теплообменника (η) характеризует количественные потери тепла, а эксергетический КПД (ηэкс) – качество потерь тепла?
3. Как вычисляется средний температурный напор для прямотока, противотока и других схем движения теплоносителей?