Файл: Учебное пособие Томск 2001 удк.doc

2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА
ПРИ СТАЦИОНАРНОМ РЕЖИМЕ

2.1. Теплопроводность плоской стенки
при граничных условиях первого рода

Дано: плоская однородная стенка толщиной δ (рис. 2.1) с постоянным коэффициентом теплопроводности λ и постоянными температурами t₁и t₂ на поверхностях.

О 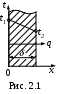пределить: уравнение температурного поля t=f (x) и плотность теплового потока q, Вт/м².

Температурное поле стенки описывается дифференциальным уравнением теплопроводности (1.3) при следующих условиях:

• 
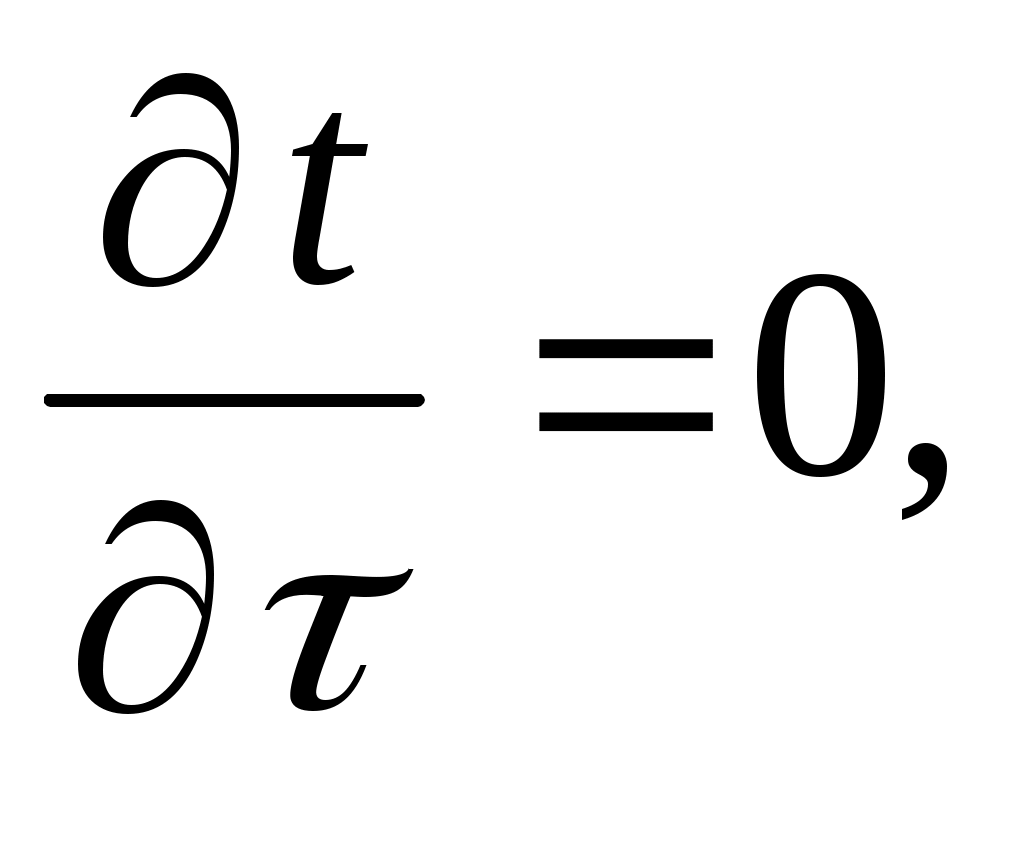  т. к. режим стационарный;
  
• 
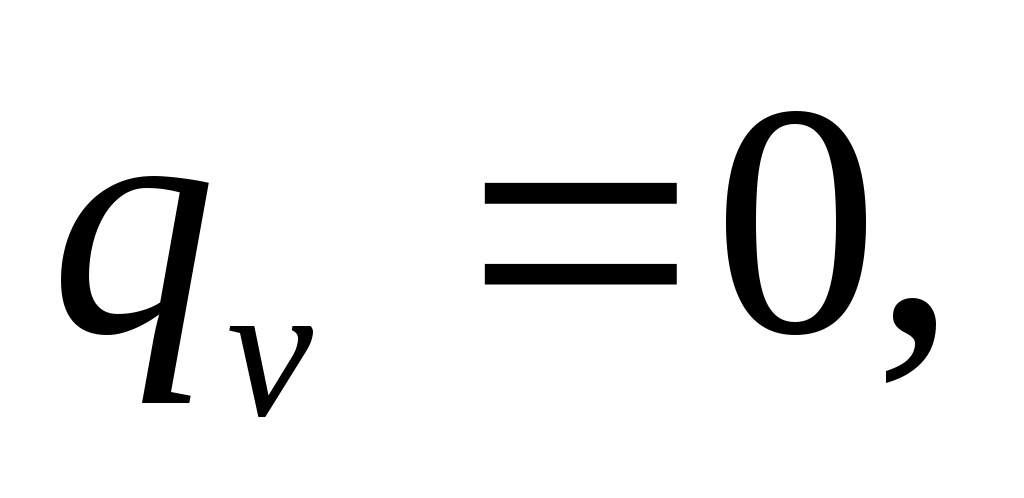  т.к. отсутствуют внутренние источники теплоты;
  
• 
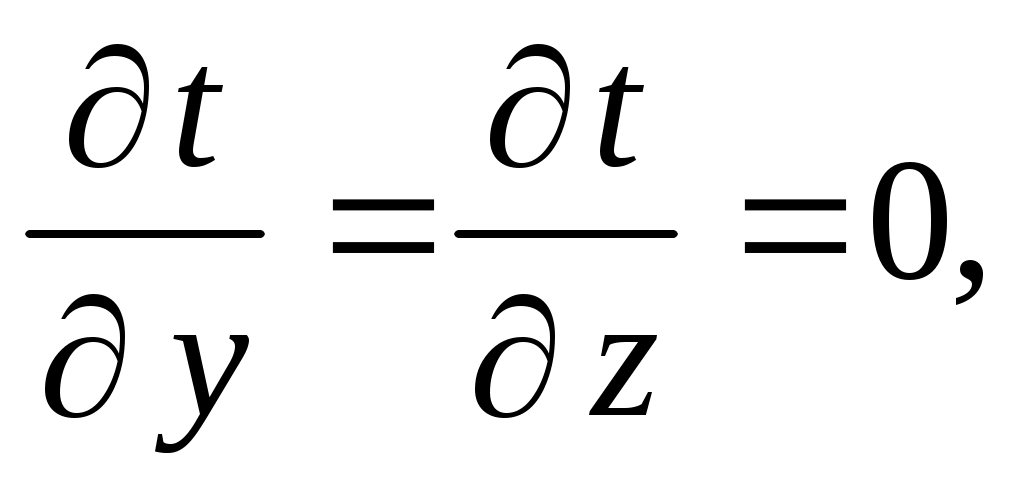  т.к. температуры t₁и t₂ на поверхностях стенки постоянны.
  

Температура стенки является функцией только одной координаты х и уравнение (1.13) принимает вид

(2.1)

т.к. коэффициент температуропроводности стенки а ≠ 0.

Граничные условия первого рода:

при х=0 t= t1 ,	(2.2)
при х= δ t= t2.	(2.3)

Выражения (2.1), (2.2), (2.3) являются математической постановкой задачи, решение которой позволит получить искомое уравнение температурного поля t= f (x).

Интегрирование уравнения (2.1) дает



При повторном интегрировании получим решение дифференциального уравнения в виде

t=с1х+с2.

(2.4)

Из уравнения (2.4) при условии (2.2) получим

t₁=с₂,

а при условии (2.3)

t₂=с₁ δ + t

---

₁ ,

откуда



Подстановка констант интегрирования с₁ и с₂ в уравнение (2.4) дает уравнение температурного поля

(2.5)

по которому можно рассчитать температуру по толщине стенки на любой координате 0<x<δ.

Зависимость t= f (x), согласно (2.5) – прямая линия (рис. 2.1), что справедливо при λ=const.

Для определения плотности теплового потока, проходящего через стенку, воспользуемся законом Фурье



С учетом получим расчетную формулу для плотности теплового потока, передаваемого через плоскую стенку,

(2.6)

Поток теплоты, передаваемый через поверхность стенки площадью F, вычисляется по формуле

(2.7)

Формулу (2.6) можно записать в виде



где

Величина называется термическим сопротивлением теплопроводности плоской стенки.

На основании уравнения

qR=t₁ – t₂

можно сделать вывод о том, что термическое сопротивление стенки прямо пропорционально перепаду температур по толщине стенки.

У честь зависимость коэффициента теплопроводности от температуры,

---

λ(t), можно, если в уравнения (2.6) и (2.7) подставить значения λ_ср для интервала температур t₁ –t₂.

Рассмотрим теплопроводность многослойной плоской стенки, состоящей, например, из трех слоев
(рис. 2.2).

Дано: δ₁ , δ₂, δ₃, λ₁, λ₂, λ₃, t₁=const, t₄=const.

Определить: q, Вт/м²; t₂, t₃.

При стационарном режиме и постоянных температурах поверхностей стенки тепловой поток, передаваемый через трехслойную стенку, можно представить системой уравнений:

	(2.8)
	(2.9)
	(2.10)

или

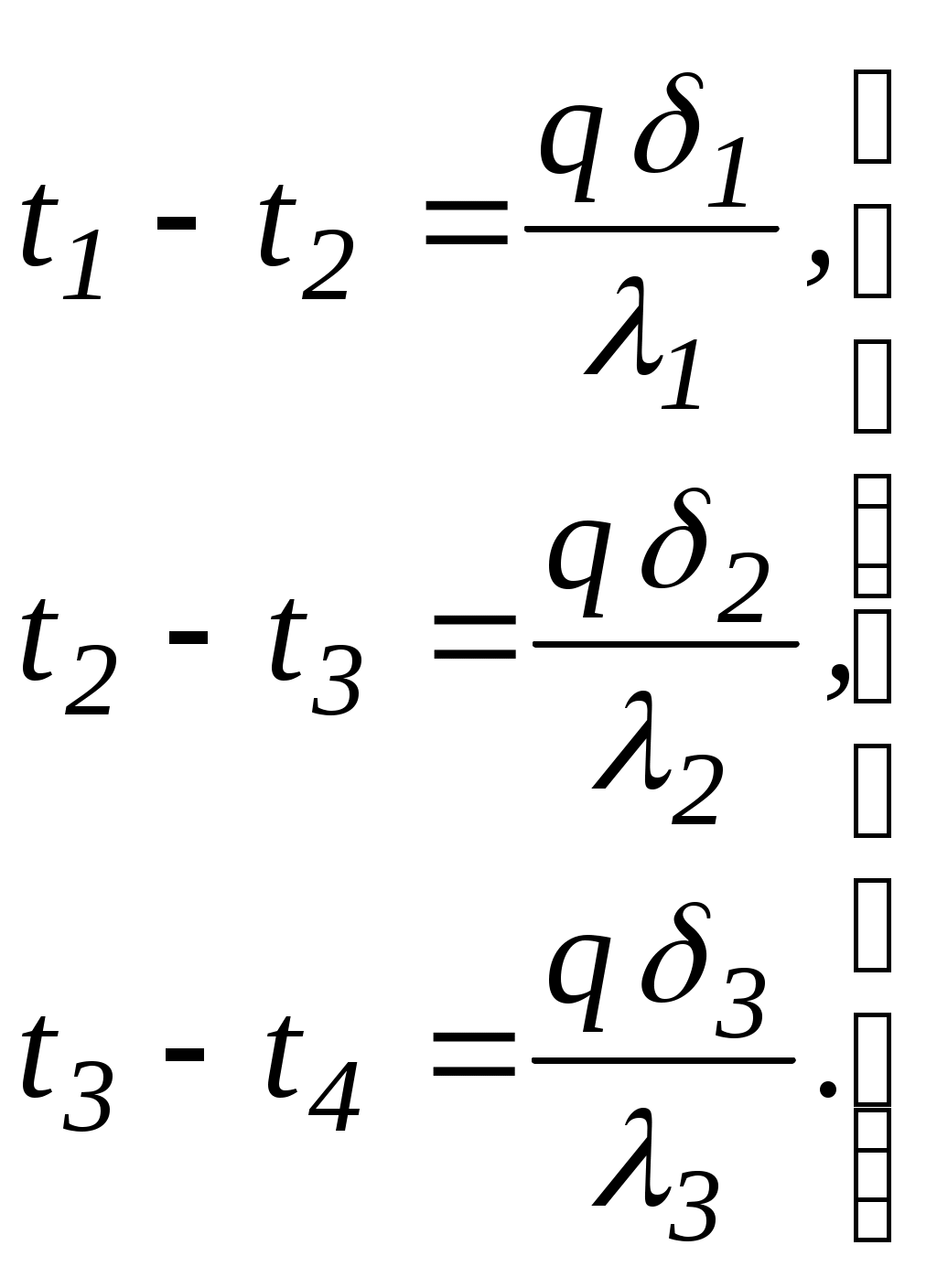(2.11)

Сложив левые и правые части уравнений (2.11), получим расчетную формулу для плотности теплового потока, передаваемого через трехслойную стенку

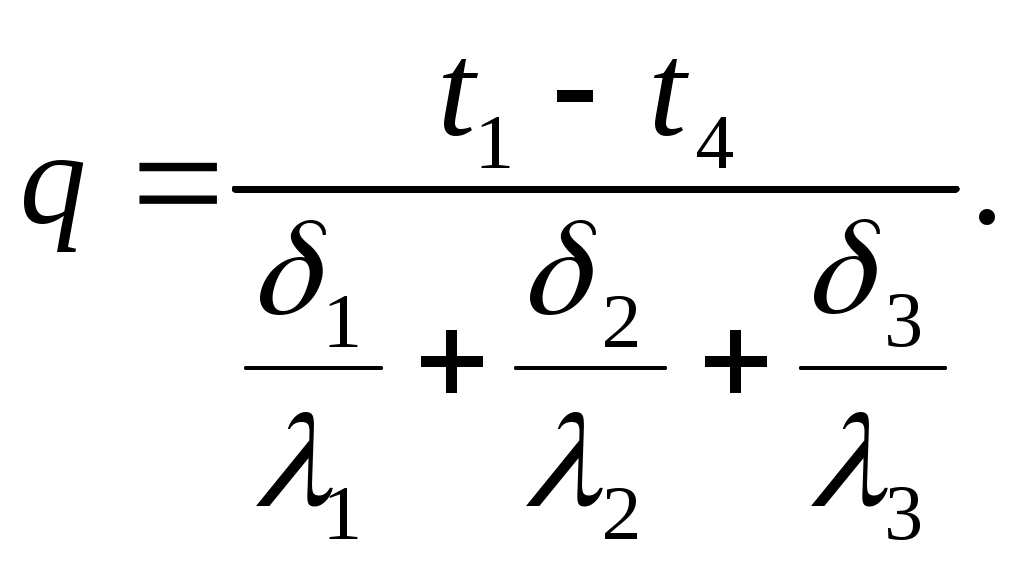(2.12)

Температуры на границах слоев t₂ и t₃ можно рассчитать по уравнениям (2.8) – (2.10) после того, как найдена плотность теплового потока (q) по (2.12).

Общий вид уравнения (2.12) для многослойной плоской стенки, состоящей из п однородных слоев с постоянными температурами на наружных поверхностях и , имеет вид

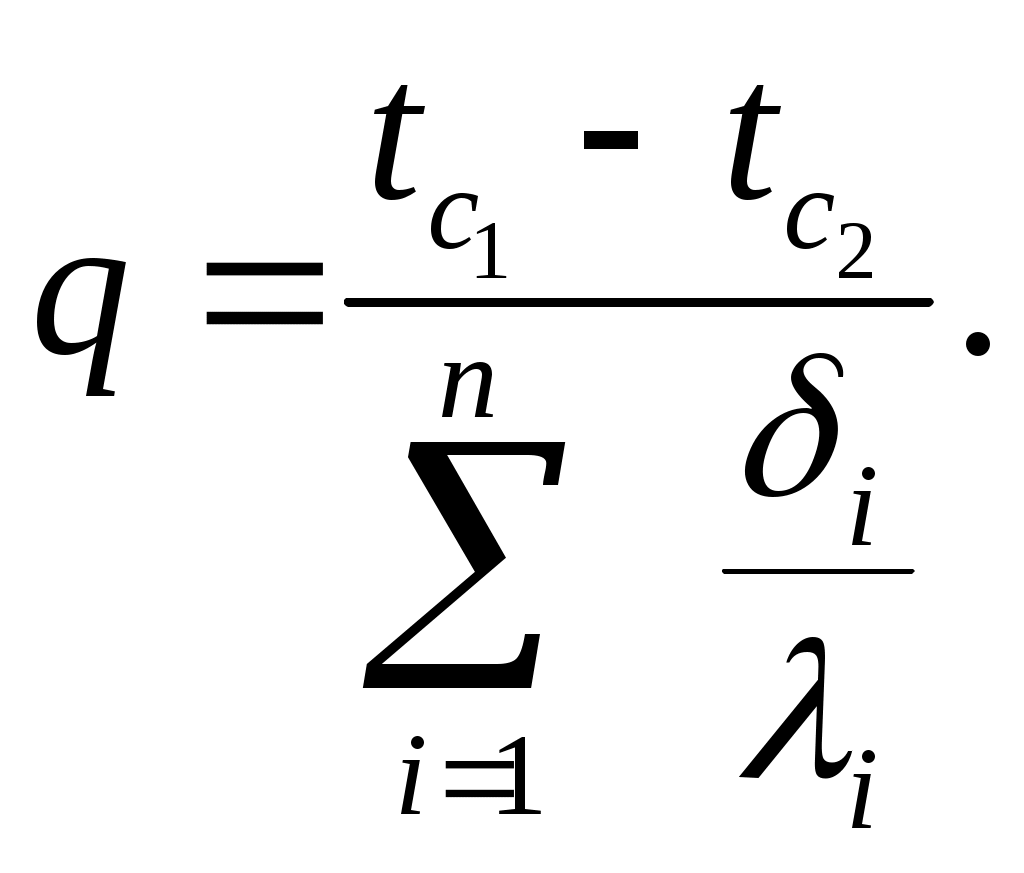(2.13)

---

Средний коэффициент теплопроводности многослойной стенки называют эффективным (λ_эф). Он равен коэффициенту теплопроводности однородной стенки, толщина и термическое сопротивление которой равны толщине и термическому сопротивлению многослойной стенки



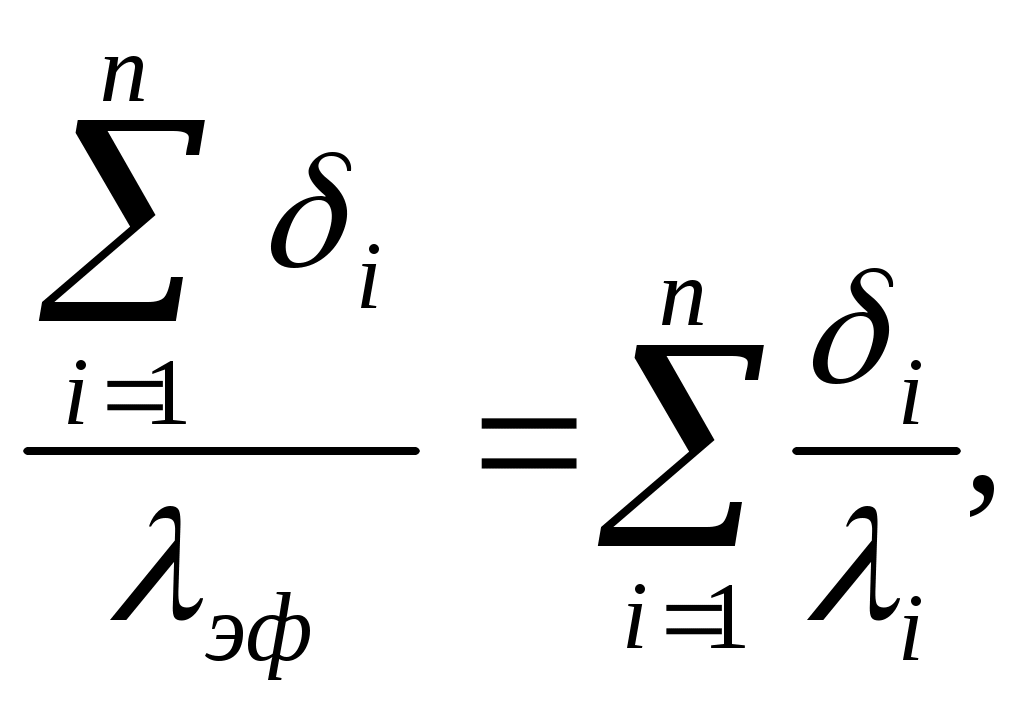
откуда

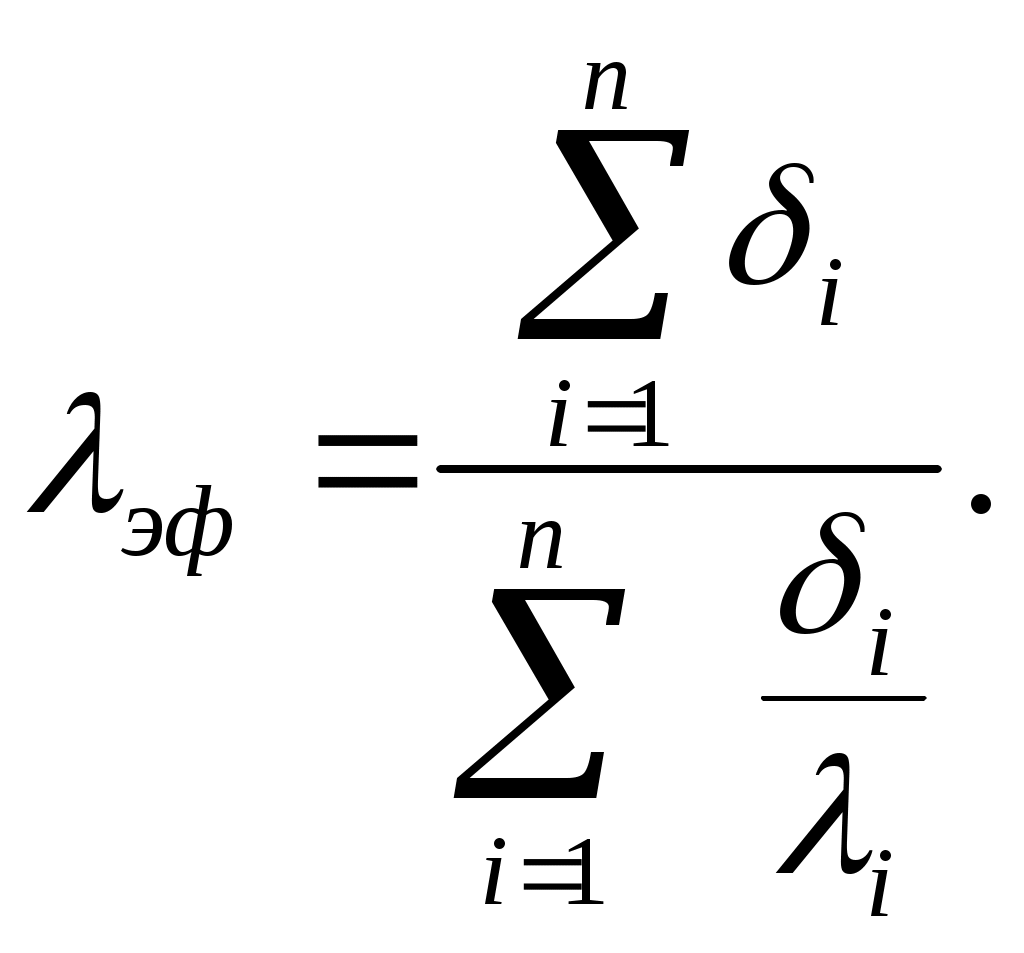(2.14)

---

2.2. Теплопроводность цилиндрической стенки
при граничных условиях первого рода

Д 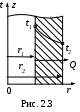ано: Однородная цилиндрическая стенка (стенка трубы) с внутренним радиусом r₁, наружным – r₂, длиной , с постоянным коэффициентом теплопроводности λ, с постоянными температурами на поверхностях t₁ и t₂.
(рис. 2.3).

Определить: уравнение температурного поля
t = f (r), тепловой поток, передаваемый через стенку
Q, Вт.

Дифференциальное уравнение теплопроводности в цилиндрических координатах (1.14) для условий данной задачи:



принимает вид

(2.15)

Граничные условия первого рода:

при r=r1 t=t1 ,	(2.16)
при r=r2 t=t2 .	(2.17)

Порядок решения системы уравнений (2.15) – (2.17) тот же, что и в случае плоской стенки: находится общий интеграл дифференциального уравнения второго порядка (2.15), который содержит две константы интегрирования
с₁и с₂ . Последние определяются с помощью граничных условий (2.16) и (2.17) и после подстановки их значений в решение дифференциального уравнения (общий интеграл) получаем уравнение температурного поля цилиндрической стенки t = f (r) в виде

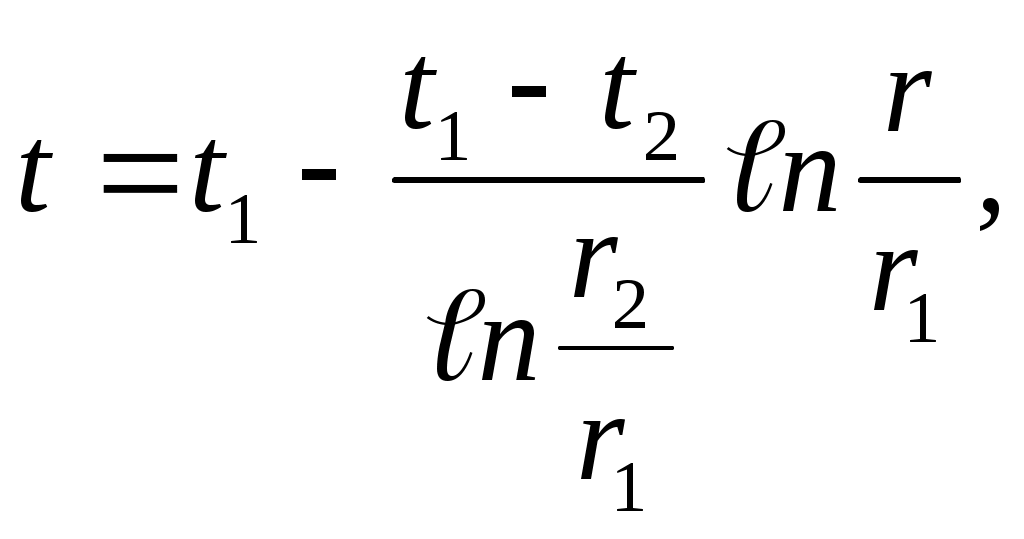(2.18)

где r₁ r r

---