ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 635
Скачиваний: 3
СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.2. Температурное поле. Градиент температуры. Тепловой поток
1.4. Дифференциальное уравнение теплопроводности
2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА ПРИ СТАЦИОНАРНОМ РЕЖИМЕ
2.1. Теплопроводность плоской стенки при граничных условиях первого рода
2.2. Теплопроводность цилиндрической стенки при граничных условиях первого рода
2.4. Критический диаметр тепловой изоляции
3. ТЕПЛОПРОВОДНОСТЬ ТЕЛ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛАПРИ СТАЦИОНАРНОМ РЕЖИМЕ
3.1. Теплопроводность однородной пластины
3.2. Теплопроводность однородного цилиндрического стержня
3.3. Теплопроводность цилиндрической стенки
4.1. Теплообмен излучением между твердыми телами, разделенными диатермичной средой
4.2. Особенности излучения газов
5.1. Теплопередача через плоскую стенкусо сложным теплообменом
5.2. Теплопередача через цилиндрическую стенкусо сложным теплообменом
5.3. Интенсификация теплопередачи
6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНАИ ОСНОВЫ ТЕОРИИ ПОДОБИЯИ МОДЕЛИРОВАНИЯ ПРОЦЕССОВ
6.1. Дифференциальные уравнения теплообмена
6.3. Моделирование теплоотдачи
6.4. Физические особенности процесса теплоотдачи
7. ТЕПЛООТДАЧА В ОДНОФАЗНОЙ СРЕДЕ
7.1. Теплоотдача при свободном движении жидкости
7.2. Теплоотдача при продольном омывании поверхности вынужденным потоком жидкости
7.3. Теплоотдача при вынужденном течении жидкости в трубах и каналах
7.4. Теплоотдача при поперечном обтекании труб
8. ТЕПЛООТДАЧА ПРИ ФАЗОВЫХ ПРЕВРАЩЕНИЯХ
8.2. Теплоотдача при конденсации
9.1. Классификация теплообменников
Нетрудно убедиться, что при подстановке в (2.18) r= r1 получим t=t1 , при r=r2 получим t=t2. Распределение температуры по толщине цилиндрической стенки, в соответствии с (2.18) подчиняется логарифмическому закону (рис. 2.3).
Для определения теплового потока воспользуемся законом Фурье:
| | (2.19) |
Если взять производную
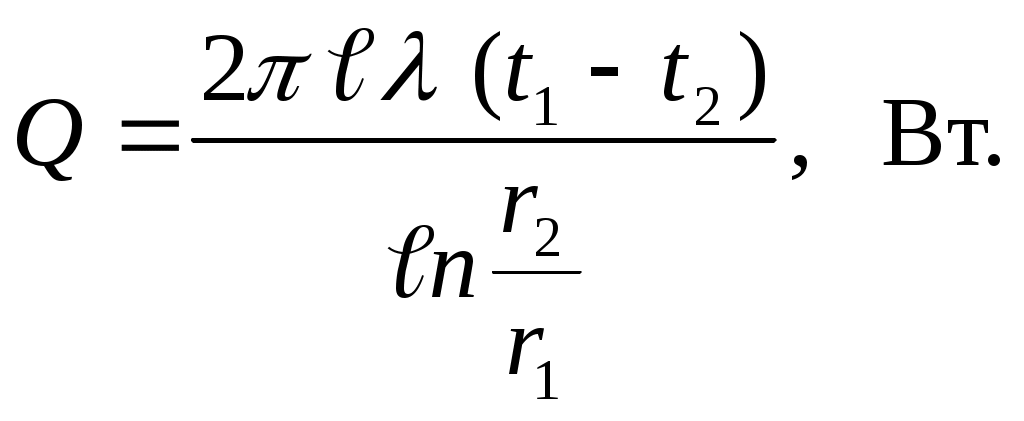 | (2.20) |
В технических расчетах часто тепловой поток вычисляется для 1 м длины трубы:
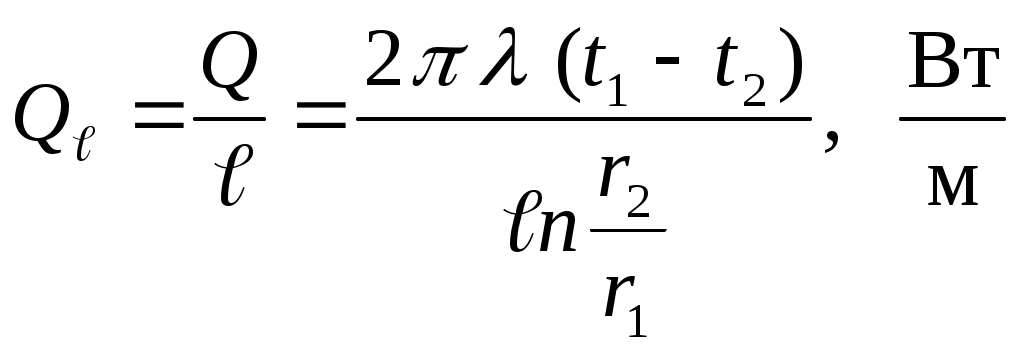
и называется линейной плотностью теплового потока.
Запишем уравнение (2.20) в виде
где
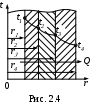
Для трехслойной цилиндрической стенки (трубы, покрытой двумя слоями тепловой изоляции) с известными постоянными температурами поверхностей (t1 и t4), с известными геометрическими размерами (r1 , r2, r3, r4 ,
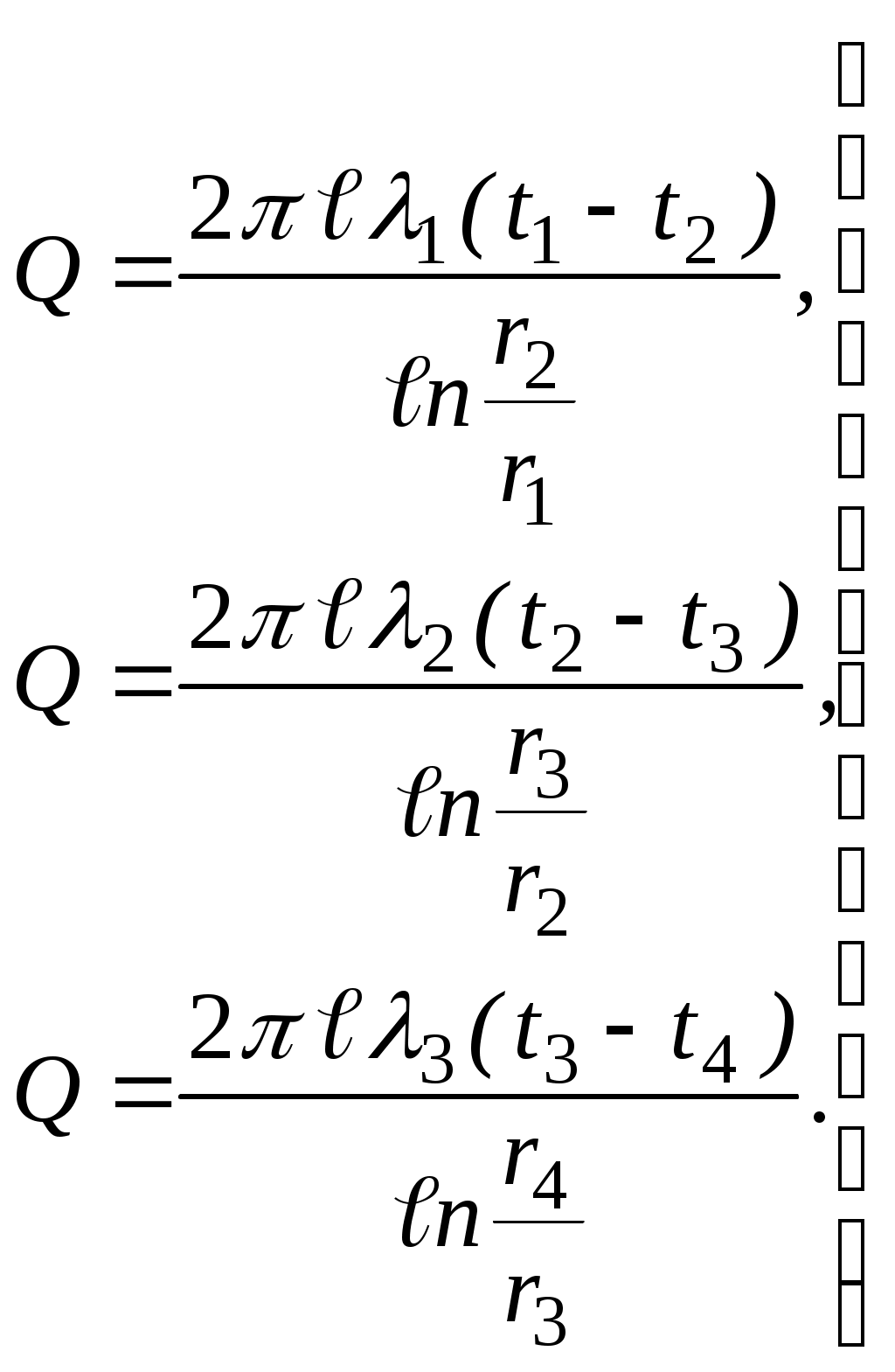 | (2.21) |
Совместное решение системы уравнений (2.21) дает расчетную формулу для теплового потока, передаваемого через трехслойную стенку при заданных температурах на поверхностях,
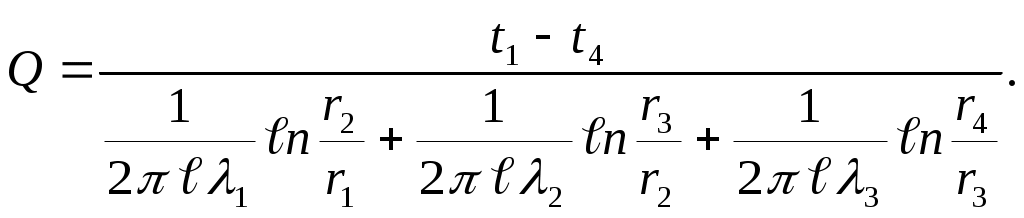 | (2.22) |
Температуры на границах слоев (t2, t3) можно рассчитать по уравнениям (2.21).
Для многослойной цилиндрической стенки, состоящей из п слоев, формулу (2.22) можно записать в общем виде
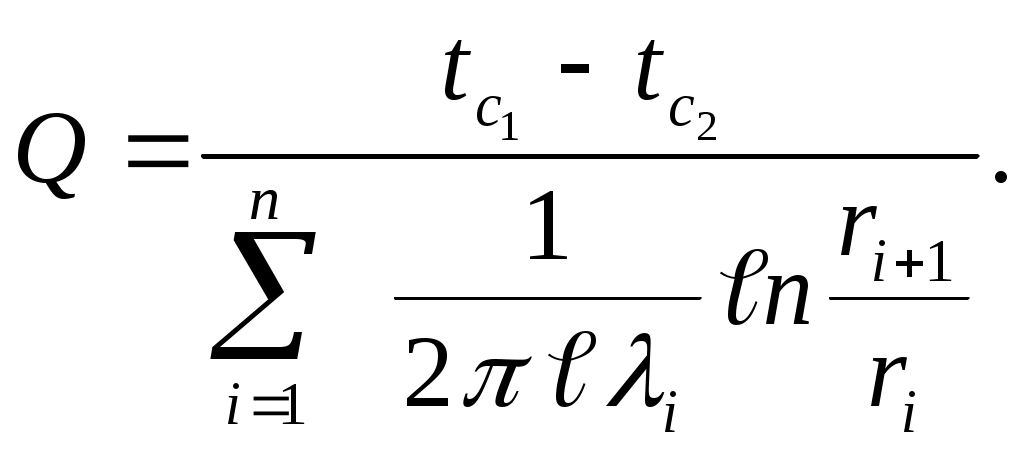 | (2.23) |
Эффективный коэффициент теплопроводности для многослойной цилиндрической стенки, как и для многослойной плоской стенки, определяется из равенства суммы термических сопротивлений многослойной стенки термическому сопротивлению однородной стенки той же толщины, что и многослойная. Так, для двухслойной тепловой изоляции трубы
(рис. 2.4) эффективный коэффициент теплопроводности (λэф) определ ится из равенства
2.3. Теплопроводность плоской и цилиндрической стенок
при граничных условиях третьего рода (теплопередача)
Граничные условия третьего рода состоят в задании температуры жидкости (tж) и коэффициента теплоотдачи (
Передача тепла от одной жидкости к другой через разделяющую их стенку называется теплопередачей.
Примерами теплопередачи служит перенос теплоты от дымовых газов к воде через стенку трубы парового котла, перенос тепла от горячей воды к окружающему воздуху через стенку батареи отопления и т.д.
Теплообмен между поверхностью и средой (теплоносителем) может быть конвективным, если теплоноситель – жидкость (вода, нефть и т.д.) или радиационно-конвективным, когда теплота передается путем конвективного теплообмена и излучением, если теплоноситель – газ (дымовые газы, воздух и т.д.).
Рассмотрим теплопередачу через плоскую и цилиндрическую стенки при условии только конвективного теплообмена на поверхностях. Теплопередача с радиационно-конвективным теплообменом (сложным теплообменом) на поверхностях будет рассмотрена позже.
Плоская стенка (рис. 2.5)
Д
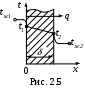 ано:
ано: Определить: q, t1, t2.
Плотность теплового потока q описывается следующими уравнениями в зависимости от способа передачи теплоты:
– от горячей жидкости к стенке
| | (2.24) |
– через стенку
| | (2.25) |
– от стенки к холодной жидкости
| | (2.26) |
Записав уравнения (2.24) – (2.26) в виде
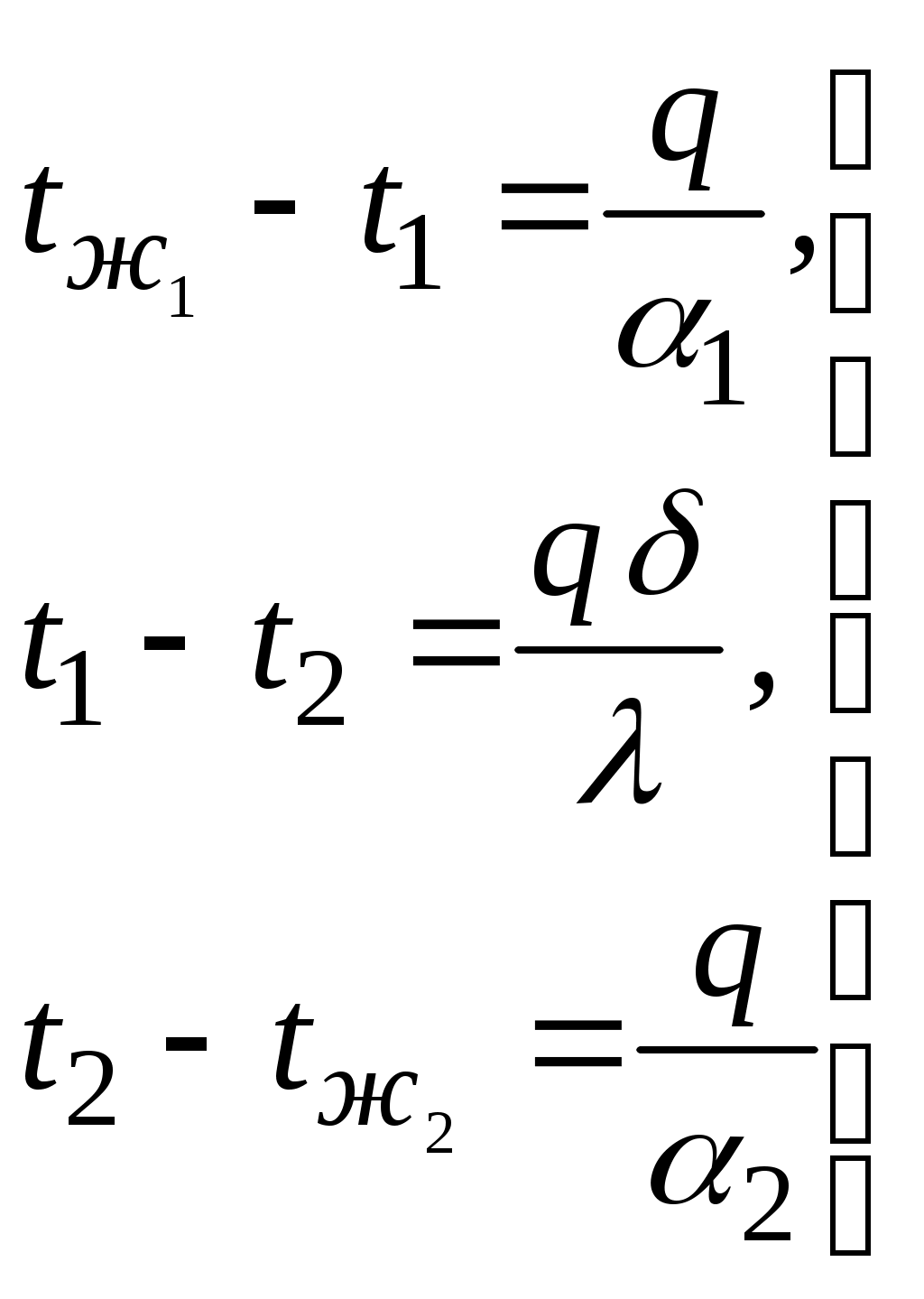 | (2.27) |
и сложив почленно правые и левые части уравнений (2.27), получим формулу для расчета теплопередачи (q, Вт/м2) через плоскую стенку в виде
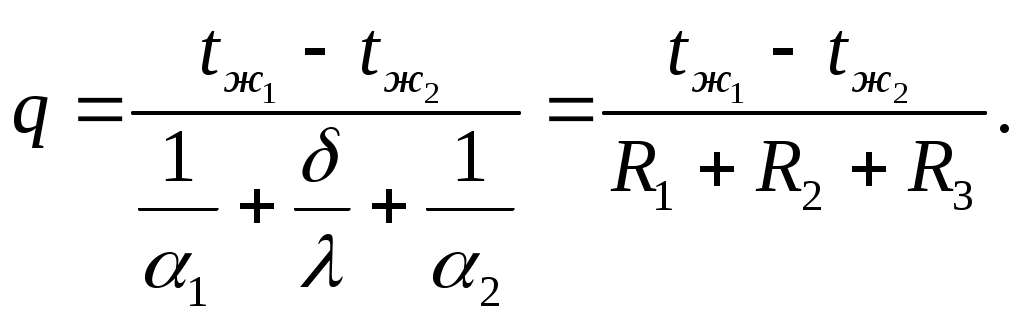 | (2.28) |
Величины
Температуры на поверхностях стенки t1 и t2 можно рассчитать по уравнениям (2.24) – (2.26) после того, как определена плотность теплового потока (q) по уравнению (2.28).
Формулу (2.28) можно записать в виде
| | (2.29) |
где
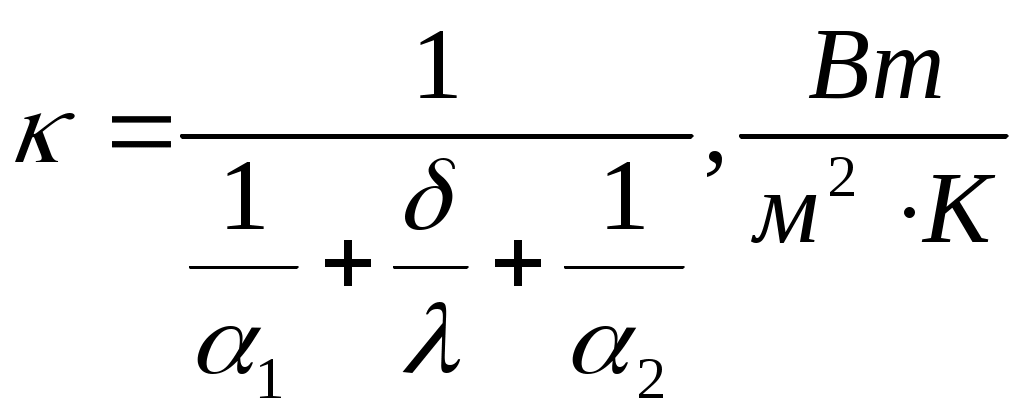 - коэффициент теплопередачи плоской стенки,характеризует интенсивность процесса теплопередачи.
- коэффициент теплопередачи плоской стенки,характеризует интенсивность процесса теплопередачи.Теплопередача через многослойную плоскую стенку рассчитывается по формуле
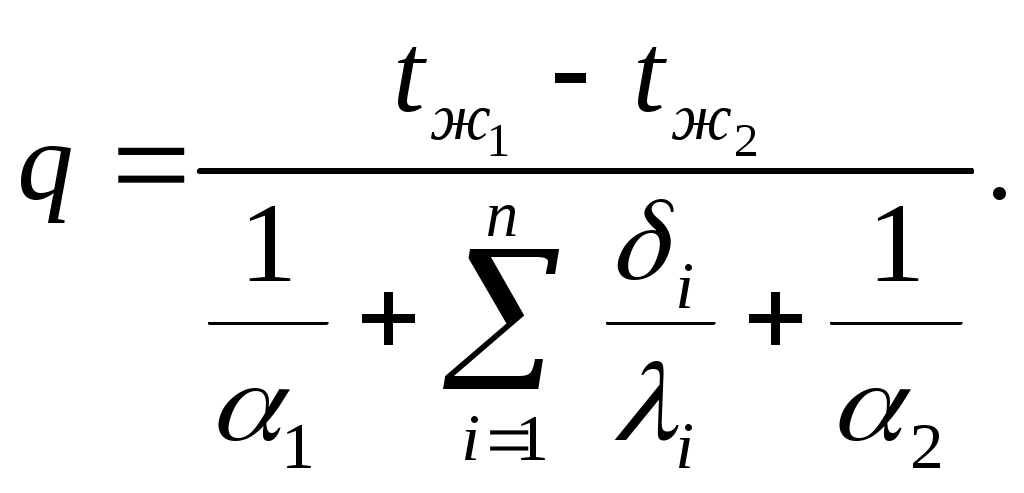 | (2.30) |
Цилиндрическая стенка (рис. 2.6)
Д
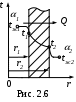 ано:
ано: Определить: Q, Вт; t1, t2.
Для цилиндрической стенки, по аналогии с плоской стенкой, можно записать следующую систему уравнений:
| | (2.31) | | |
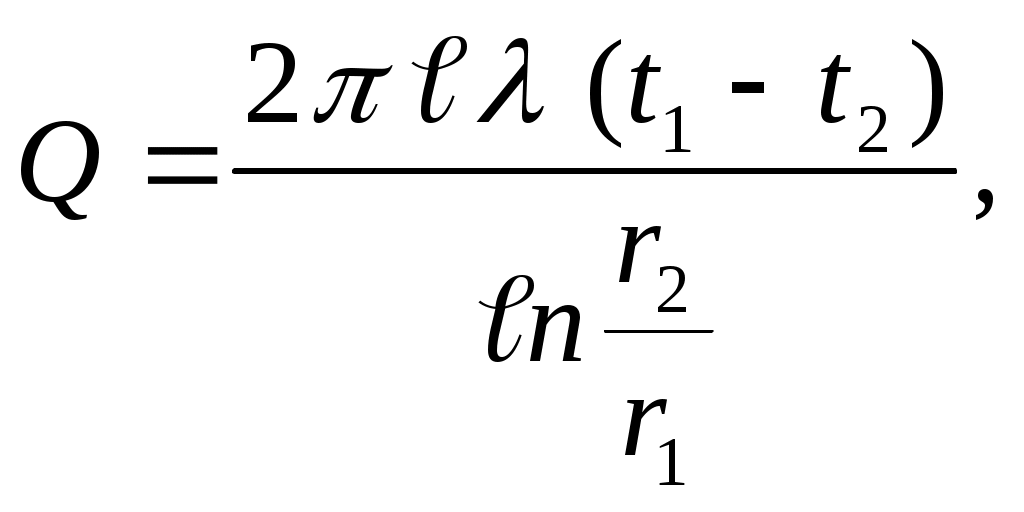 | (2.32) | | |
| | (2.33) | ||
где
Записав уравнения (2.31) – (2.33) относительно разностей температур, а затем сложив правые и левые части уравнений, получим формулу для расчета теплопередачи (Q, Вт) через цилиндрическую стенку в виде
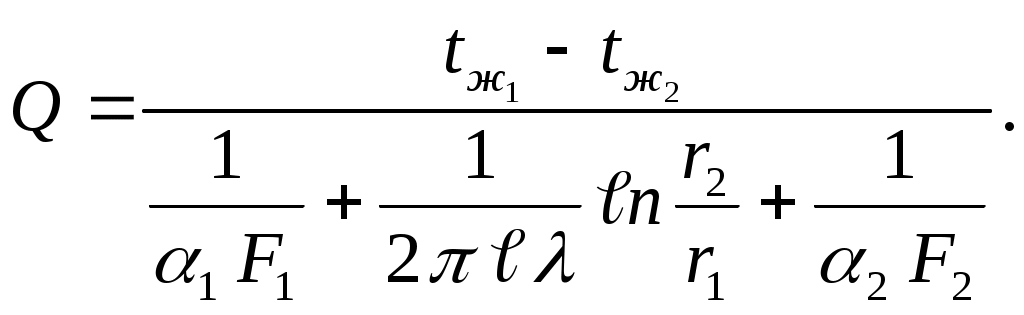 | (2.34) |
Температуры на поверхностях стенки t1и t2 рассчитываются по уравнениям (2.31) – (2.33).
Формулу (2.34) также можно представить в виде
| где 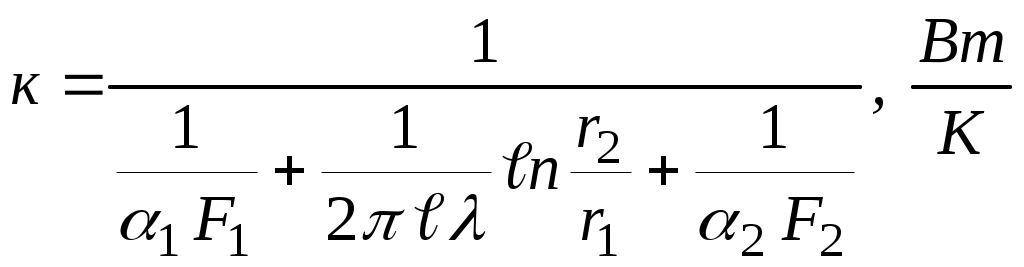 – коэффициент теплопередачи цилиндрической стенки. – коэффициент теплопередачи цилиндрической стенки. |
Для металлических труб с
где
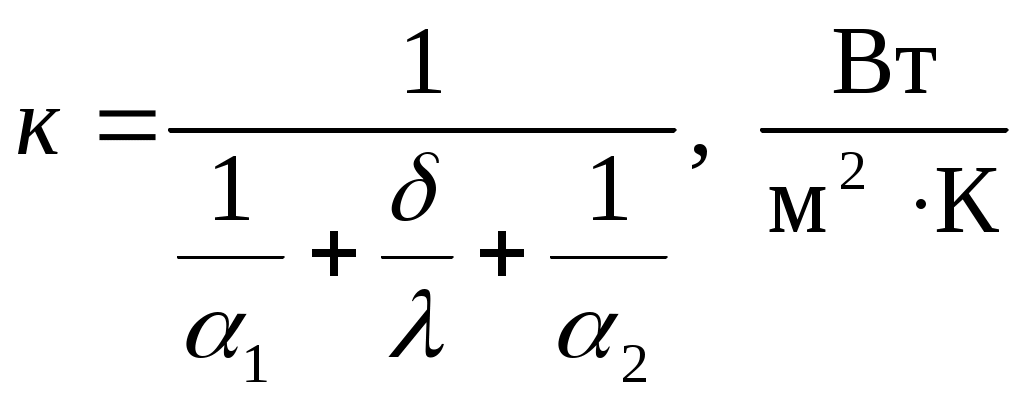 .
.Диаметр dx=d1 , если 1<<2 ;