Файл: Учебное пособие Томск 2001 удк.doc

где V= (r₂²- r₁²) , м³ – тепловыделяющий объем.

Охлаждение только по внутренней поверхности (рис. 3.5)

Д 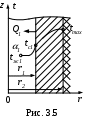ано: r₁, _, r₂ . , q_v, λ, , .

Определить: t=f(r), Q₁, Вт.

Граничное условие третьего рода для внутренней поверхности стенки запишется в виде

(3.35)

Условие максимума температуры на наружной поверхности стенки

(3.36)

Решением системы уравнений (3.23), (3.35), (3.36) является уравнение температурного поля t=f(r)

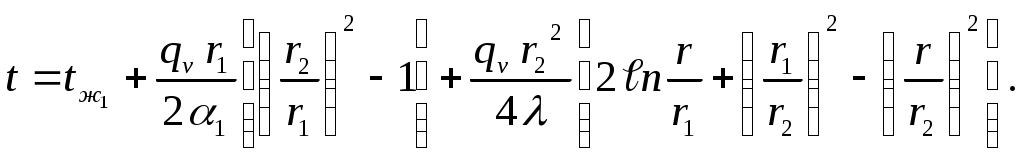(3.37)

Расчетные формулы для t_max и можно получить, если в (3.37) подставить r=r₂ и r=r₁ соответственно.

Тепловой поток Q₁,рассеиваемый внутренней поверхностью стенки, рассчитывается по уравнению (3.34).
Охлаждение по внутренней и наружной поверхностям (рис. 3.6)

Д 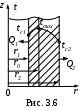ано: r₁, _, r₂ . , q_v, λ,

---

, .

Определить: t=f(r), радиус максимальной температуры r₀ , тепловые потоки Q₁ , Q₂.
Для нахождения постоянных интегрирования с₁и с₂ в уравнении (3.26) и радиуса максимальной температуры r₀ потребуется три дополнительных условия: граничные условия первого рода на поверхностях стенки

при	(3.38)
при	(3.39)

и условие максимума температуры при r =r₀

(3.40)

Решением системы уравнений (3.23), (3.38) - (3.40) являются уравнение температурного поля стенки t=f(r)

(3.41)

где r – текущий радиус, и формула для расчета радиуса максимальной температуры

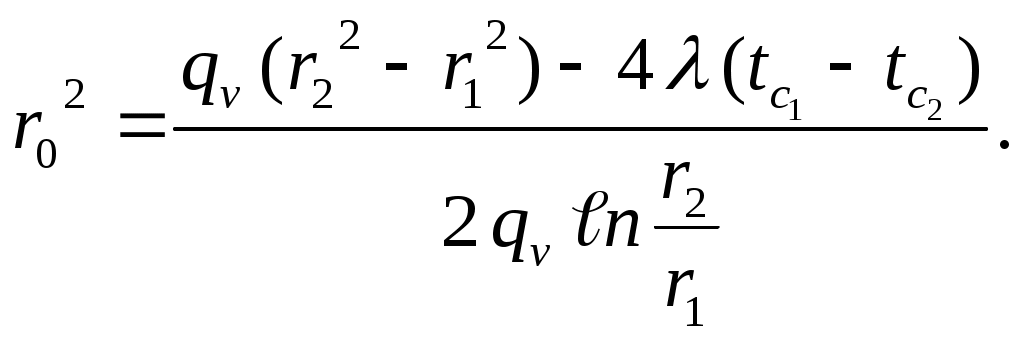(3.42)

Формулы для расчета перепадов температуры в стенке получены на основании (3.41):

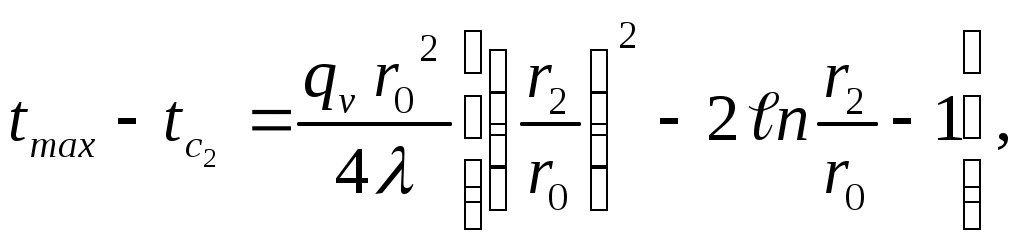(3.43)

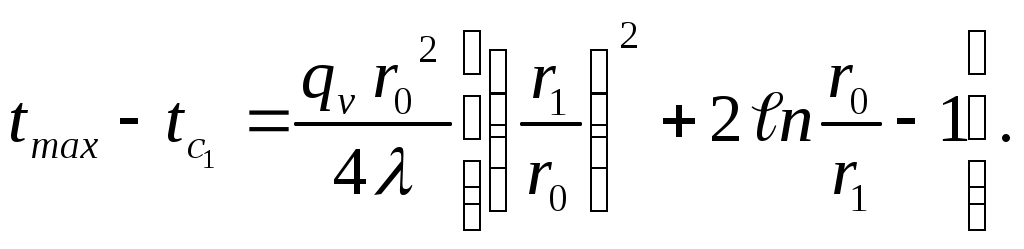(3.44)

Потоки теплоты Q₁ и Q₂, рассеиваемые поверхностями стенки, рассчитываются по формулам

	(3.45)
	(3.46)

---

Суммарный тепловой поток

(3.47)

Контрольные задания

1. 
   Рассчитайте объемную плотность внутреннего тепловыделения
   (q_v, Вт/м³) стальной шины с размерами 3х100х1000 мм при допустимой нагрузке I=300A. Удельное электрическое сопротивление материала шины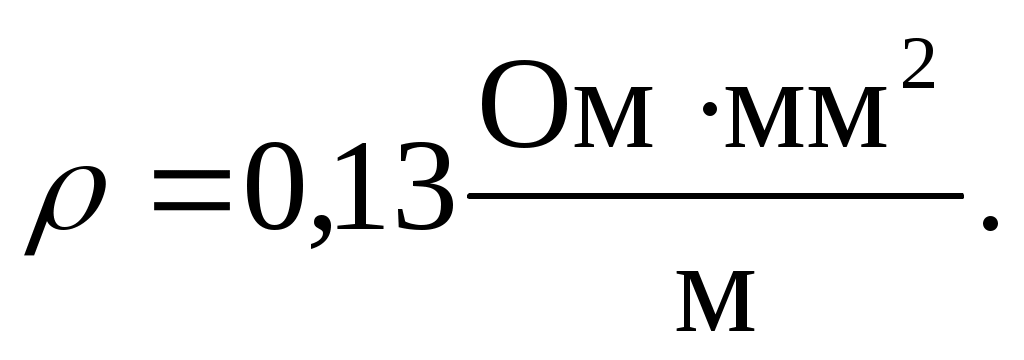
   

Ответ: q_v=1,310⁵ Вт/м³.

2. 
   Сделайте подстановку значения t_c в уравнение (3.10) и убедитесь, что правые части уравнений (3.10) и (3.11) одинаковы.
   
3. 
   Запишите формулы для расчета температур и на поверхностях пластины при несимметричных условиях ее охлаждения и граничных условиях третьего рода, используя уравнение температурного поля (3.15).
   
4. 
   Запишите формулу для расчета максимальной температуры (t_max) пластины при несимметричных условиях охлаждения и граничных условиях первого рода, используя уравнение температурного поля (3.21).
   
5. 
   Рассчитайте плотность внутреннего тепловыделения (q_v, Вт/м³), тепловой поток (Q, Вт), рассеиваемый поверхностью цилиндрического нихромового стержня диаметром d=5 мм, длиной =420 мм при напряжении U=10В и электрическом сопротивлении R=0,025 Ом.
   

Ответы: q_v=4,8310⁸ Вт/м³; Q=N=4000 Вт.

6. 
   Для цилиндрической стенки с охлаждением только по наружной поверхности, используя уравнение температурного поля (3.33), получите расчетные формулы для t_max ,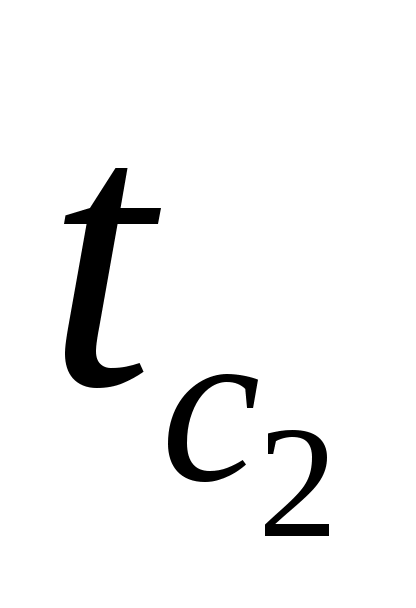 , t_max - .
   
7. 
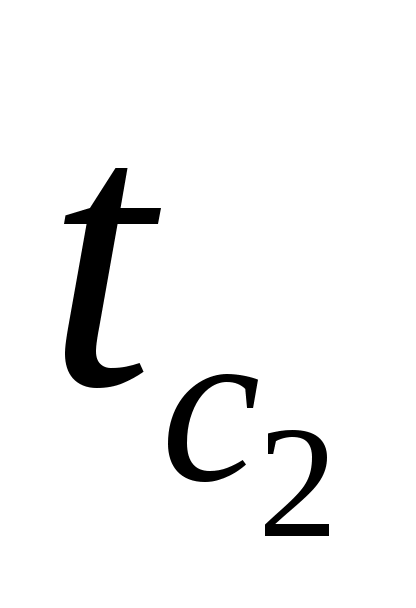   Для цилиндрической стенки с охлаждением только по внутренней поверхности, используя уравнение температурного поля (3.37), получите расчетные формулы для t_max , , t_max - .
   
8. 
   Сделайте вывод формул (3.43) и (3.44), и убедитесь в их правильности.
   

---

Задачи для самостоятельного решения

Задача № 1. По электрическому нагревателю, выполненному из константановой ленты сечением 1 х 6 мм² и длиной 1м протекает электрический ток I=20 А, U=200 В.

Определить температуру поверхности ленты (t_c) и середины сечения по толщине (t_тах), если коэффициент теплоотдачи на поверхности нагревателя =1000 Вт/м²∙К, температура среды t_ж=100^оС, коэффициент теплопроводности константа =20Вт/м∙К.

Рассчитать плотность теплового потока (q,Вт/м²), отводимого от поверхности нагревателя.

Примечание. Необходимые формулы для расчета содержатся в разделе 3.1.

Ответы: t_c=433,3^оС; t_тах=437,5^оС; q=3,33∙10⁵ Вт/м².
Задача № 2. Тепловыделяющий элемент ядерного реактора выполнен из смеси карбида урана и графита в виде цилиндрического стержня диаметром d=12мм. Плотность внутреннего тепловыделения q_v=3,88∙10⁸ Вт/м³. Теплопроводность материала стержня λ=58 Вт/м∙К.

Определить температуру (t_c) и плотность теплового потока (q,Вт/м²) на поверхности стержня, если его максимальная температура 2000^оС.

Примечание. Формулы, необходимые для расчета, содержатся в разделе 3.2.

Ответы: t_c=1939,8^оС; q=1,164∙10⁶ Вт/м².

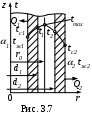
П ример решения задачи
Тепловыделяющий элемент выполнен из урана (λ=31 Вт/м∙К) в форме трубы (рис. 3.7) с внутренним диаметром d₁=16 мм, наружным d₂=26 мм.

Объемная плотность тепловыделения q_v=5∙10⁷ Вт/м³. Поверхности ТВЭЛа покрыты плотно прилегающими оболочками из нержавеющей стали (λ_с=21Вт/м∙К) толщиной δ=0,5 мм. ТВЭЛ охлаждается двуокисью углерода (СО₂) по внутренней и наружной поверхностям оболочек с t_ж1 =200^оС и t_ж2=240^оС. Коэффициенты теплоотдачи от поверхностей оболочек к газу

---

α₁=520 Вт/м²∙К, α₂=560 Вт/м²∙К.

Определить максимальную температуру ТВЭЛа (t_тах), температуры на поверхностях оболочек ( и ) и на поверхностях урана (t₁и t₂), а также потоки тепла (Q₁и Q₂), отводимые от поверхности ТВЭЛа в расчете на длину =1м.

Решение

Тепловыделяющий элемент представляет собой цилиндрическую стенку с внутренним тепловыделением, охлаждаемую по наружной и внутренней поверхностям (раздел 3.3). При наличии стальных оболочек на поверхностях ТВЭЛа и с учетом исходных данных можно записать следующую систему уравнений:

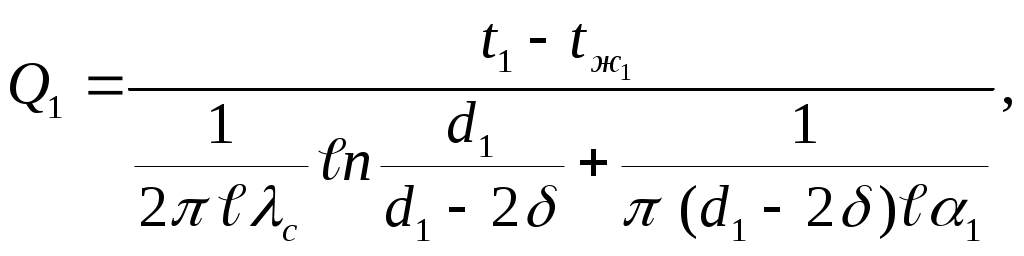	(3.48)
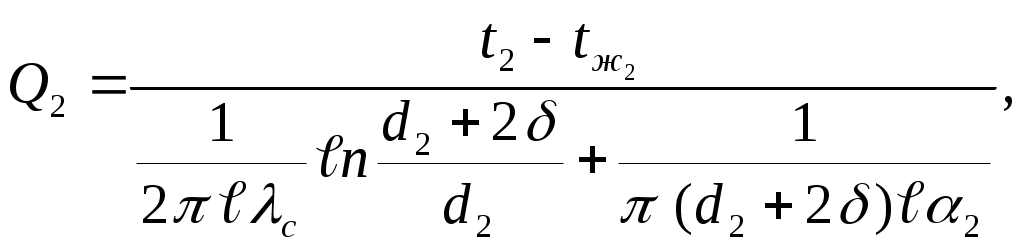	(3.49)
,	(3.50)
	(3.51)
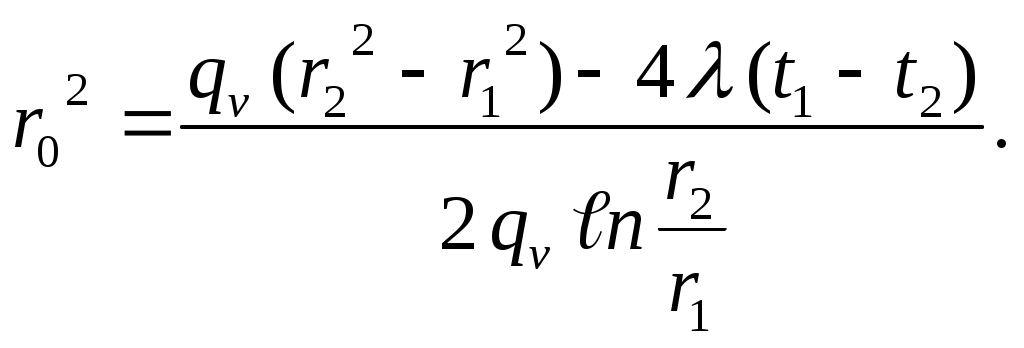	(3.52)

Система уравнений (3.48) – (3.52) содержит 5 неизвестных: Q₁, Q₂, t₁, t₂, r₀ и решается методом взаимных подстановок. В результате решения определяются искомые величины:

Q₁=6286 Вт, Q₂=10199 Вт, t₁=459^оС, t₂=458^оС, r₀=10,2 мм.

Температуры на поверхностях стальных оболочек ( ), а также максимальная температура ТВЭЛа (t_тах) рассчитываются по формулам

---