Файл: Учебное пособие Томск 2001 удк.doc

позволяет получить безразмерные комплексы, называемые числами подобия:

- число Нуссельта, характеризует интенсивность конвективного теплообмена;

, м – геометрический размер;

- число Рейнольдса, характеризует отношение сил инерции к силам вязкости;

- число Прандтля, характеризует теплофизические свойства жидкости;

- число Грасгофа, характеризует отношение подъемной силы, возникающей вследствие разности плотностей жидкости благодаря перепаду температур Δt, к силам вязкости;

- число Фруда, характеризующее отношение инерционных сил к силам тяжести, и т.д.

Число Нуссельта (Nu) является определяемым числом в задачах конвективного теплообмена, т.к. содержит искомую величину – коэффициент теплоотдачи . Остальные числа подобия (Re, Pr, Gr, Fr…) называются определяющими и включают в себя величины, от которых зависит коэффициент теплоотдачи.

Таким образом,

Nu=f(Re,Pr,Gr,Fr…).

(6.6)

Функциональная зависимость между числами подобия типа (6.6) называется уравнением подобия. По уравнению подобия можно найти число Nu и рассчитать коэффициент теплоотдачи.

Основные положения теории подобия формулируются в виде трех теорем:

1. 
   Подобные процессы должны иметь одинаковую физическую природу и описываться одинаковыми дифференциальными уравнениями.
   
2. 
   Условия однозначности подобных процессов (геометрические, физические, граничные и т.д.) должны быть одинаковы во всем, кроме численных значений размерных постоянных.
   
3. 
   Одноименные определяющие числа подобия подобных процессов должны иметь одинаковую численную величину (Re'=Re", Gr'=Gr" и т.д.).
   

---

Теорию подобия можно рассматривать как учение об обобщенных безразмерных переменных, характеризующих данный процесс.

---

6.3. Моделирование теплоотдачи

Моделированием называется метод экспериментального изучения явления на модели натурного образца. Чтобы процессы в модели и образце были подобны, необходимо выполнить условия подобия:

1. 
   моделировать процессы, имеющие одинаковую физическую природу и описываемые одинаковыми дифференциальными уравнениями;
   
2. 
   обеспечить одинаковые условия однозначности в модели и образце;
   
3. 
   обеспечить равенство одноименных чисел подобия для модели и образца.
   

Результаты эксперимента обрабатывают в числах подобия, а связь между ними представляют в виде уравнений подобия. Обычно это степенные зависимости типа

Nuжd=C Reжdп Pr жт,

(6.7)

где С, п, т – постоянные коэффициенты, определяются экспериментально. Индексы d и ж указывают на определяющий размер (d) и определяющую температуру (t_ж), т.е.


Определяющий размер – это чаще всего геометрический размер, который оказывает наибольшее влияние на теплоотдачу.

Величины, зависящие от температуры (, v, Pr…), должны браться из справочника при определяющей температуре, в данном случае - при t_ж. В качестве определяющей может быть и другая температура (t_c, ).

По уравнениям подобия типа (6.7) определяется число Нуссельта и рассчитывается коэффициент теплоотдачи.

6.4. Физические особенности процесса теплоотдачи

Процесс теплоотдачи – это конвективный перенос теплоты между поверхностью и омывающей ее средой. Его принято описывать с помощью уравнения Ньютона-Рихмана: количество теплоты, передаваемой с поверхности площадью dF за промежуток времени dτ в среду с температурой t_ж ,определяется выражением

---

Уравнение Ньютона-Рихмана для теплового потока при постоянных , t_с , t_ж имеет вид

(6.8)

для плотности теплового потока оно запишется так:

(6.9)

Явление конвективного переноса теплоты наблюдается лишь в движущихся средах.
Факторы, влияющие на теплоотдачу:

1. Природа возникновения движения (свободное или вынужденное).

Свободное движение, или естественная конвекция возникает под действием разности плотностей холодных и нагретых частиц жидкости или газа (подъемно – опускное движение у поверхности тела).

Вынужденное движение (вынужденная конвекция) возникает под действием разности давлений, создаваемой насосом, компрессором и т.д. В некоторых случаях, наряду с вынужденным, одновременно может развиваться свободное движение. Относительное влияние последнего тем больше, чем больше разность температур в отдельных объемах жидкости и чем меньше скорость вынужденного движения.
2. Режим течения жидкости (ламинарный, турбулентный, переходный).

П
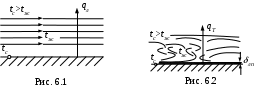
ри ламинарном режиме частицы жидкости движутся послойно, не перемешиваясь (рис. 6.1), перенос теплоты от стенки к жидкости осуществляется теплопроводностью (q_л=q_ТП). Турбулентный режим характеризуется непрерывным перемешиванием всех слоев жидкости (рис. 6.2).

При этом у поверхности стенки образуется ламинарный подслой жидкости толщиной _лп. Перенос теплоты от стенки к жидкости с турбулентным течением осуществляется теплопроводностью и конвекцией (q_т=q_тп+ q_к).

Режим движения жидкости, промежуточный между ламинарным и турбулентным, называется

---

переходным.
3. Гидродинамический и тепловой пограничный слои

При любом режиме движения частицы жидкости, непосредственно прилегающие к твердой поверхности, как бы прилипают к ней. В результате вблизи обтекаемой поверхности под действием сил вязкого трения образуется плоский слой заторможенной жидкости, в пределах которого скорость жидкости изменяется от нуля (на поверхности тела) до скорости невозмущенного потока (вдали от тела). Этот слой заторможенной жидкости называется гидродинамическим пограничным слоем.

Н 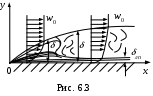а рис. 6.3 дана схема образования гидродинамического пограничного слоя при продольном омывании поверхности потоком жидкости с постоянной скоростью ω₀.

На начальном участке поверхности, как правило, течение жидкости ламинарное (ламинарный пограничный слой). По мере удаления от входной кромки толщина гидродинамического пограничного слоя δ увеличивается. Утолщение пограничного слоя происходит с увеличением вязкости жидкости. Рост толщины пограничного слоя приводит к уменьшению его устойчивости и на определенном расстоянии от входной кромки он переходит в турбулентный. Убывание скорости в турбулентном пограничном слое можно охарактеризовать как умеренное, в ламинарном подслое – резкое.

Гидродинамический пограничный слой (слой заторможенной жидкости), режим течения жидкости в нем влияют на коэффициент теплоотдачи. Чем меньше толщина гидродинамического пограничного слоя δ, тем выше коэффициент теплоотдачи .

Аналогично понятию гидродинамического пограничного слоя существует понятие теплового пограничного слоя. Это слой жидкости (δ_т), прилегающий к твердой поверхности, в пределах которого температура жидкости изменяется от температуры стенки (t_с) до температуры потока вдали от поверхности (t_ж).

В общем случае толщина гидродинамического (δ) и теплового (δ_т) пограничных слоев не совпадает и только для газов практически одинакова. Соотношение толщины теплового и гидродинамического пограничных слоев определяется значением числа .

Дифференциальное уравнение теплоотдачи (6.1) описывает передачу тепла в тонком пристеночном слое жидкости. В первом приближении градиент температуры в тепловом пограничном слое можно выразить так:

---