Файл: Учебное пособие Томск 2001 удк.doc

тогда коэффициент теплоотдачи определится соотношением

т.е. коэффициент теплоотдачи прямо пропорционален теплопроводности жидкости и обратно пропорционален толщине теплового пограничного слоя.
4. Теплофизические свойства жидкости

Коэффициент теплоотдачи зависит от коэффициента теплопроводности (λ), теплоемкости (с_р), кинематической вязкости (v), плотности (ρ), коэффициента объемного расширения (β) и других свойств жидкости, в частности, при наличии фазовых переходов (кипения, конденсации), от теплоты парообразования (r), коэффициента поверхностного натяжения () и т.д.

5. Геометрические размеры, форма, ориентация поверхности теплообмена

Установлено, что коэффициент теплоотдачи зависит от геометрической формы поверхности тела (плоской, цилиндрической, шаровой или иной), размеров (протяженности поверхности, диаметра трубы или сферы и т.д.), ориентации поверхности теплообмена (вертикальной, горизонтальной с теплоотдачей вверх, горизонтальной с теплоотдачей вниз, наклонной и т.д.).

Контрольные вопросы и задания

1. 
   Запишите дифференциальные уравнения конвективного теплообмена, поясните физический смысл слагаемых в уравнениях энергии и движения.
   
2. 
   Сформулируйте условия подобия физических явлений. Что дает теория подобия?
   
3. 
   Каковы условия физического моделирования теплоотдачи и что оно дает?
   
4. 
   Что называется определяющей температурой и определяющим размером?
   
5. 
   Докажите, что числа подобия безразмерны, путем подстановки размерности величин, входящих в них.
   
6. 
   Дайте понятия гидродинамического и теплового пограничных слоев. Как толщина этих слоев влияет на коэффициент теплоотдачи?
   
7. 
   Как влияют на теплоотдачу: а) теплопроводность жидкости;
   б) вязкость жидкости?
   
8. 
   Перечислите факторы, влияющие на коэффициент теплоотдачи.
   

---

Примеры решения задач

Задача № 1. Моделируется процесс теплоотдачи при течении нефти по нефтепроводу диаметром d=1020 мм со скоростью w=0,5м/с. Кинематическая вязкость нефти для исследуемого участка трубы при средней температуре =30^оС составляет v=14,710^-6м²/с.

В модели предполагается нефть заменить водой, диаметр трубки d=30мм.

Какой расход воды необходимо иметь в модели, чтобы обеспечить подобие процессов теплоотдачи в модели и образце?

Решение

Согласно третьей теоремы подобия одноименные числа подобия для модели и образца должны быть одинаковы (Re_м=Re_o), т.е.



Кинематическая вязкость воды при =30^оС v=0,80510^-6м²/с (табл. 2 приложения). Тогда скорость воды



расход воды



Плотность воды ρ_м=995,7 кг/м³ взята из табл. 2 приложения при =30^оС.

Задача №2. На воздушной модели парового котла, выполненной в масштабе 1/8 натуральной величины, производилось изучение теплоотдачи конвекцией. Для первого газохода модели при различных скоростях воздуха были получены следующие значения коэффициента теплоотдачи:

w, м/с 2,0 3,14 4,65 8,8

, Вт/м²∙К 50,4 68,6 90,6 141.

Средняя температура воздуха, проходяшего через модель, t_ж=20^оС. Диаметр трубок модели d=12,5мм.

Коэффициент теплоотдачи при обработке опытных данных был отнесен к средней арифметической разности температур между воздухом и стенкой.

На основе опытных данных получите формулу для расчета теплоотдачи конвекцией в первом газоходе котла в виде зависимости Nu

---

_жd=C Re_жd ⁿ.

Решение

Результаты эксперимента обработаем в числах подобия

и .

При t_ж=20^оС для воздуха коэффициент теплопроводности λ=0,026 Вт/м∙К, кинематическая вязкость v=15,06∙10^-6м²/с (табл.1 приложения).

Результаты вычисления чисел Nu и Re для соответствующих значений и w представлены ниже:

w, м/с , Вт/м²∙К Re Nu

2,0 50,4 1660 24,2

3,14 68,6 2600 33,0

4,65 90,6 3860 43,6

8,8 141 7300 68,0.

По этим данным строим зависимость Nu = f (Re) в логарифмических координатах (рис. 6.4).

П 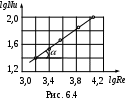о тангенсу угла наклона прямой к оси абсцисс



определяем показатель степени п=0,706.

Постоянную С находим из уравнения



Таким образом, получаем расчетную формулу

Nu_жd=0,129 ,

справедливую в пределах 1600 Re_жd 7300.

---

7. ТЕПЛООТДАЧА В ОДНОФАЗНОЙ СРЕДЕ

7.1. Теплоотдача при свободном движении жидкости

Большую роль как в технике, так и в быту играют процессы теплообмена при естественной конвекции, возникающей из-за разности плотностей нагретых и холодных частиц. Характерная картина свободного движения жидкости вдоль горячей вертикальной поверхности показана на рис. 7.1.

Н 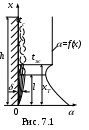агреваясь у поверхности высотой h (t_c>t_ж) жидкость, вследствие уменьшения ее плотности, поднимается вверх. Слой нагретой движущейся жидкости (δ) является одновременно гидродинамическим и тепловым пограничным слоем, т.к. в пределах этого слоя изменяется скорость (от нуля на стенке до максимума и снова до нуля на границе с неподвижной жидкостью) и температура от (t_c до t_ж.).

Вначале толщина пограничного слоя мала и ее течение носит ламинарный характер. Постепенно в движение увлекается все большее количество жидкости, толщина ламинарного слоя растет, затем он разрушается (переходный режим) и возникает турбулентный режим течения жидкости. При ламинарном режиме коэффициент теплоотдачи с увеличением толщины пограничного слоя (δ) уменьшается (рис. 7.1), при переходном режиме – резко возрастает и далее, при турбулентном режиме, по высоте поверхности сохраняется постоянным.

На основе математического описания процесса конвективного теплообмена при естественной конвекции выявлена структура уравнения подобия

Nu=f(Gr, Pr),

(7.1)

а в результате экспериментального исследования теплоотдачи установлено, что при 10³<(Gr_жх∙Pr_ж) 10⁹ – ламинарный режим течения жидкости в пограничном слое;

(Gr_жх∙Pr_ж) 6∙10¹⁰ – турбулентный режим;

10⁹<(Gr_жх∙Pr_ж) 10¹⁰ – переходный режим.

Число

---

Грасгофа рассчитывается по формуле

(7.2)

где - температурный коэффициент объемного расширения, = t_c - t_ж . Для капельных жидкостей значения =f(t) приводятся в справочной литературе, для газов – рассчитываются по формуле

полученной на основе совместного решения уравнений

и

Числа Прандтля, зависящие только от теплофизических свойств жидкостей, приводятся для различных теплоносителей (жидкостей, газов) в справочной литературе.

При расчетах произведения (Gr_жх∙Pr_ж) определяющей температурой является температура жидкости (t_ж), определяющим размером – координата х.

Для расчета коэффициентов теплоотдачи рекомендуются следующие уравнения:

• 
  При ламинарном режиме, 10³<(Gr_жх∙Pr_ж) 10⁹, локальные коэффициенты теплоотдачи ( ), описываемые кривой =f(x), рис.7.1, в ламинарной области пограничного слоя, рассчитываются по уравнению
  

---