ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 50
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 2
Задание 1.
-
перепишем систему уравнений в матричном виде и решим его методом Гаусса
1 -1 2 -1
3 2 -2 -4
5 -2 4 -1
-
от 2 строки отнимаем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 5
1 -1 2 -1
0 5 -8 -1
0 3 -6 4
-
2-ую строку делим на 5
1 -1 2 -1
0 1 -1.6 -0.2
0 3 -6 4
-
к 1 строке добавляем 2 строку, умноженную на 1; от 3 строки отнимаем 2 строку, умноженную на 3
1 0 0.4 -1.2
0 1 -1.6 -0.2
0 0 -1.2 4.6
-
3-ую строку делим на -1.2
1 0 0.4 -1.2
0 1 -1.6 -0.2
0 0 1 - 23
6
-
от 1 строки отнимаем 3 строку, умноженную на 0.4; к 2 строке добавляем 3 строку, умноженную на 1.6
1 0 0 1
3
0 1 0 - 19
3
0 0 1 - 23
6
x1 = 1
3
x2 = - 19
3
x3 = - 23
6
∆ = 1 -1 2
3 2 -2
5 -2 4 = 1·2·4 + (-1)·(-2)·5 + 2·3·(-2) - 2·2·5 - 1·(-2)·(-2) - (-1)·3·4 = 8 + 10 - 12 - 20 - 4 + 12 = -6
∆1 = -1 -1 2
-4 2 -2
-1 -2 4 = (-1)·2·4 + (-1)·(-2)·(-1) + 2·(-4)·(-2) - 2·2·(-1) - (-1)·(-2)·(-2) - (-1)·(-4)·4 = -8 - 2 + 16 + 4 + 4 - 16 = -2
∆2 = 1 -1 2
3 -4 -2
5 -1 4 =1·(-4)·4 + (-1)·(-2)·5 + 2·3·(-1) - 2·(-4)·5 - 1·(-2)·(-1) - (-1)·3·4 = -16 + 10 - 6 + 40 - 2 + 12 = 38
∆3 = 1 -1 -1
3 2 -4
5 -2 -1 = = 1·2·(-1) + (-1)·(-4)·5 + (-1)·3·(-2) - (-1)·2·5 - 1·(-4)·(-2) - (-1)·3·(-1) = -2 + 20 + 6 + 10 - 8 - 3 = 23
x1 = ∆1 = -2 = 1
∆ -6 3
x2 = ∆2 = 38 = - 19
∆ -6 3
x3 = ∆3 =23= - 23
∆ -6 6
Задача 2.
Запишем систему в виде расширенной матрицы:
| 1 | -2 | 2 | -1 | 0 |
| 1 | -3 | 1 | -4 | -5 |
| 2 | -5 | 3 | -5 | -5 |
Умножим 2-ю строку на (-1). Добавим 2-ю строку к 1-й:
| 0 | 1 | 1 | 3 | 5 |
| 1 | -3 | 1 | -4 | -5 |
| 2 | -5 | 3 | -5 | -5 |
Умножим 2-ю строку на (2). Умножим 3-ю строку на (-1). Добавим 3-ю строку к 2-й:
| 0 | 1 | 1 | 3 | 5 |
| 0 | -1 | -1 | -3 | -5 |
| 2 | -5 | 3 | -5 | -5 |
Работаем со столбцом №2.
Добавим 2-ю строку к 1-й:
| 0 | 0 | 0 | 0 | 0 |
| 0 | -1 | -1 | -3 | -5 |
| 2 | -5 | 3 | -5 | -5 |
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.
|
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.
|
Теперь исходную систему можно записать так:
x2 = [-5-( - x3 - 3x4)]/(-1)
x1 = [-5-( - 5x2 + 3x3 - 5x4)]/2
Необходимо переменные x3,x4 принять в качестве свободных переменных и через них выразить остальные переменные.
Для получения частного решения, приравняем переменные x3,x4 к 0.
Из 2-й строки выражаем x2
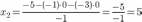
Из 3-й строки выражаем x1