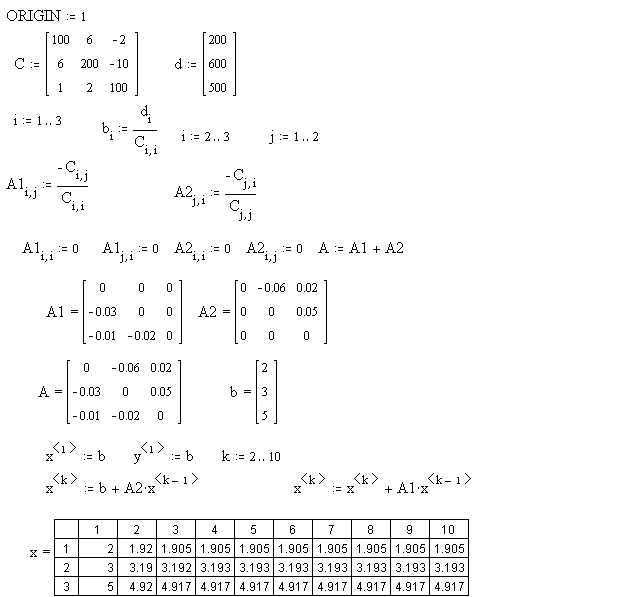Файл: Руководство по выполнению лабораторных работ по предмету Вычислительная математика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 128
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
А квадратная и невырожденная.
Предварительно приведем систему (2.2) к итерационному виду:
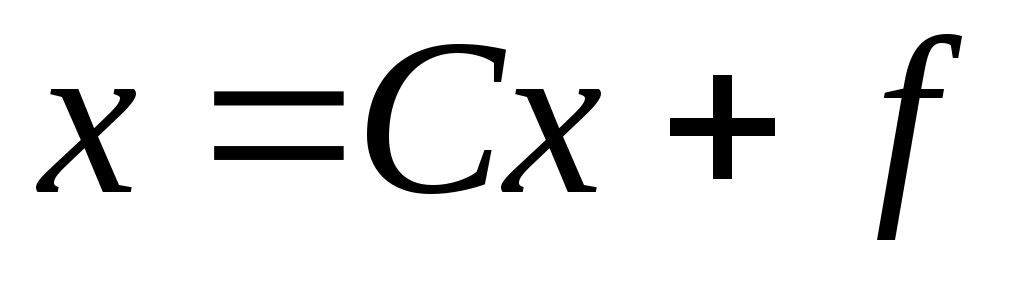 (2.3)
(2.3)
Для произвольного начального вектора итерационный процесс
итерационный процесс
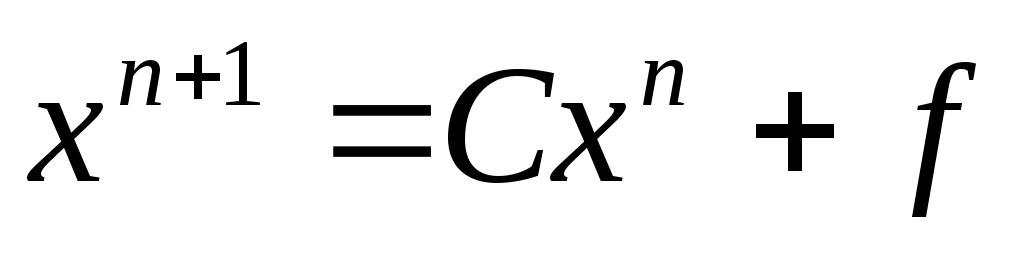
сходится, если выполнено одно из условий [2]
а) (2.4)
(2.4)
б)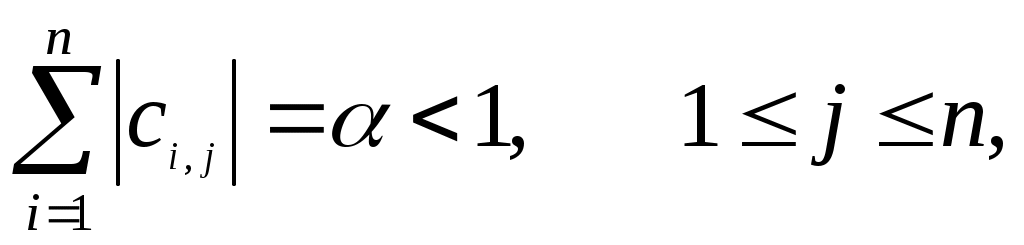 (2.5)
(2.5)
в)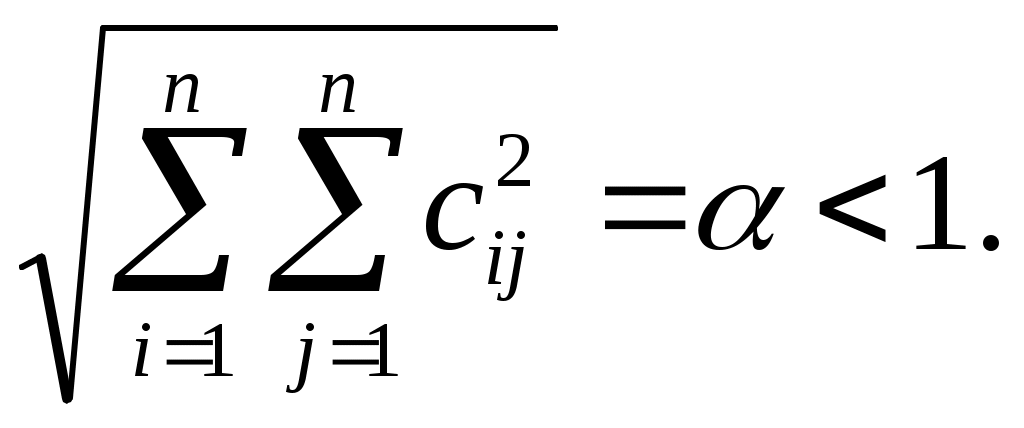 (2.6)
(2.6)
Процесс вычислений заканчиваем при выполнении условия
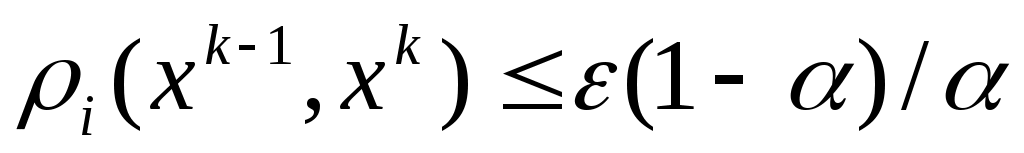 (2.7)
(2.7)
где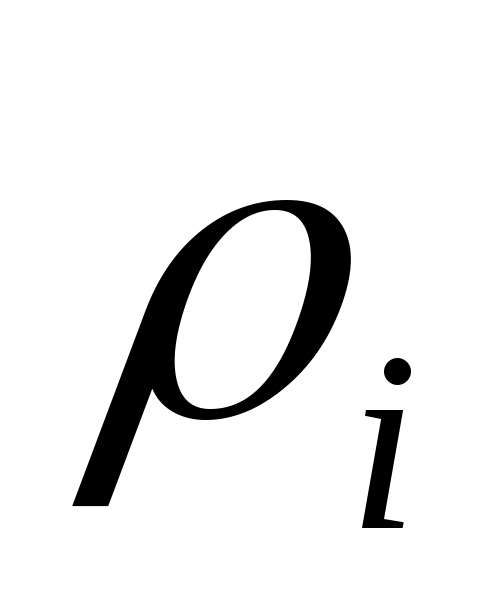 (i=1,2,3) одна из метрик, определяемая левой частью (2.4)-(2.6), по которой была установлена сходимость,
(i=1,2,3) одна из метрик, определяемая левой частью (2.4)-(2.6), по которой была установлена сходимость,  заданная точность (
заданная точность (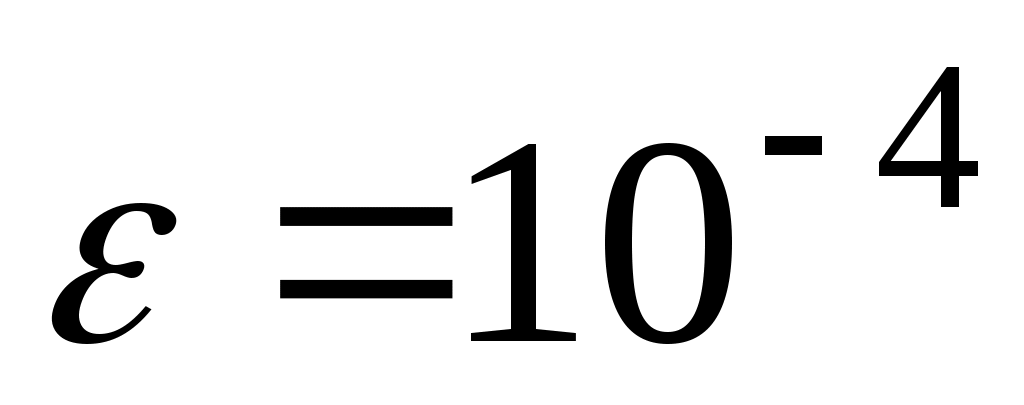 ).
).
Задание 3
Решить систему (2.1) методом Зейделя.
Метод Зейделя отличается от метода простой итерации тем, что найдя какое-то значение для компоненты, мы на следующем шаге используем его для отыскания следующей компоненты. Вычисления ведутся по формуле
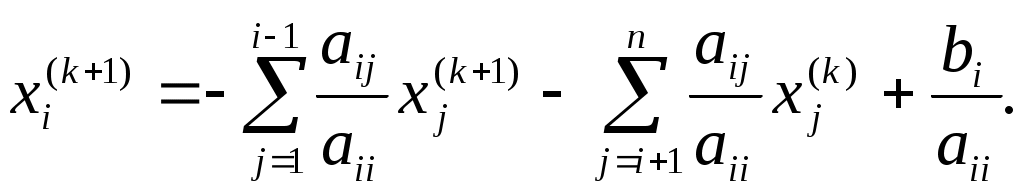 (2.8)
(2.8)
Каждое из условий (2.4)-(2.6) является достаточным для сходимости итерационного процесса по методу Зейделя. Практически же удобнее следующее преобразование системы (2.2). Домножая обе части (2.2) на АТ, получим эквивалентную ей систему
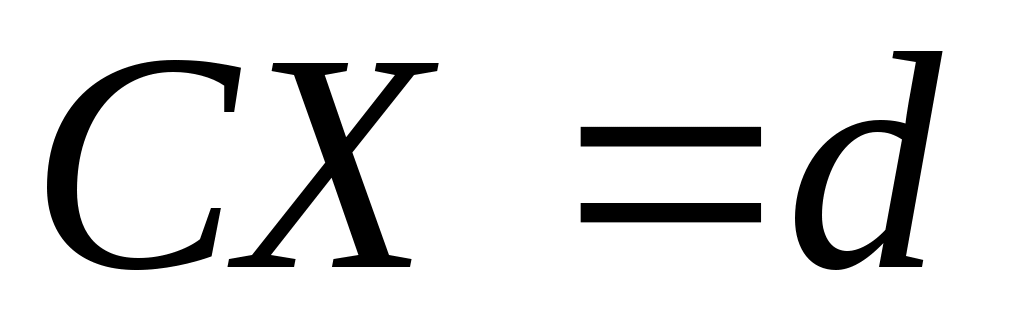 ,
,
где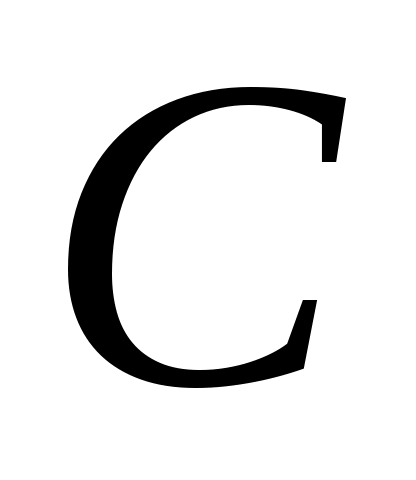 =
=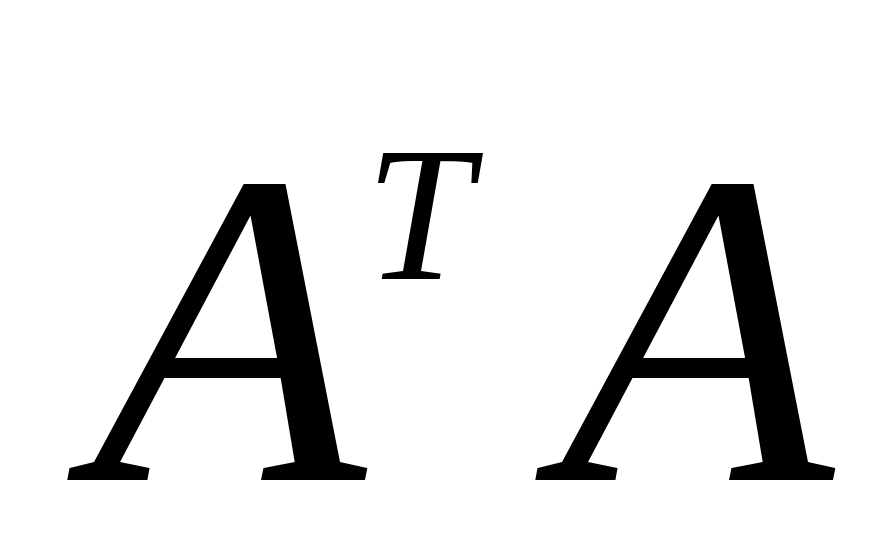 и d=
и d=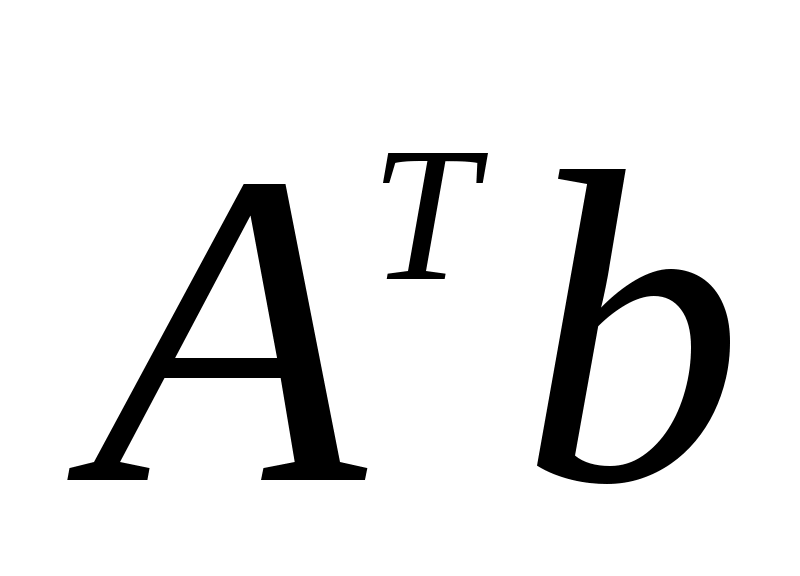 . Далее, поделив каждое уравнение на
. Далее, поделив каждое уравнение на 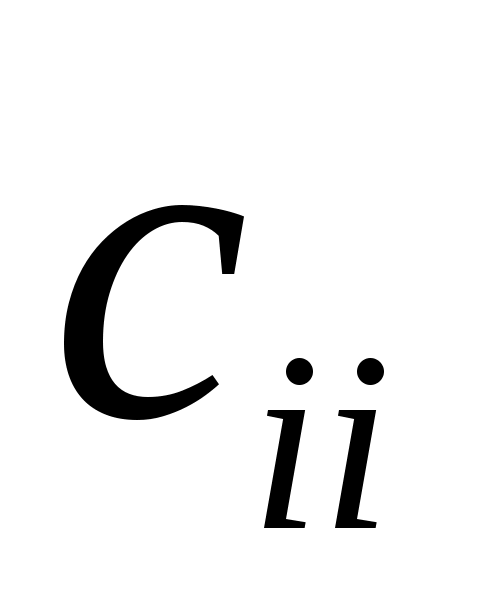 , приведем систему к виду (2.8). Подобное преобразование также гарантирует сходимость итерационного процесса.
, приведем систему к виду (2.8). Подобное преобразование также гарантирует сходимость итерационного процесса.
Примерный вариант выполнения лабораторной работы
Пример. Решите систему уравнений
X1+2X2+3X3=7,
X1-3X2+2X3=5,
X1+X2+X3=3.
1. Символьное решение систем уравнений
Фрагмент рабочего документа с соответствующими вычислениями приведен ниже. Здесь = - логическое равенство.
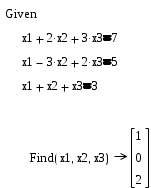
2. Решение системы линейных алгебраических уравнений как матричное уравнение Ax=b
Порядок выполнения задания.
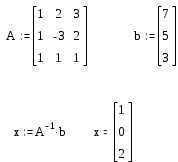
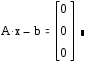
Решим систему с помощью функции lsolve и сравним результат с решением x=A-1b.
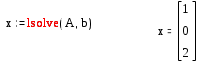
Комментарии. Функция augment(A,b) формирует расширенную матрицу системы добавлением к матрице системы справа столбца правых частей. Функция rrefприводит расширенную матрицу системы к ступенчатому виду, выполняя прямой и обратный ходы гауссова исключения. Последний столбец содержит решение системы.
Порядок выполнения работы.
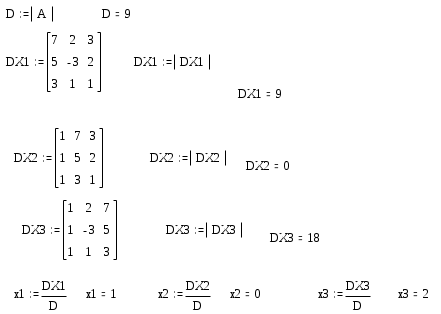
5.Решение системы линейных алгебраических уравнение методом простых итераций
Порядок выполнения задания
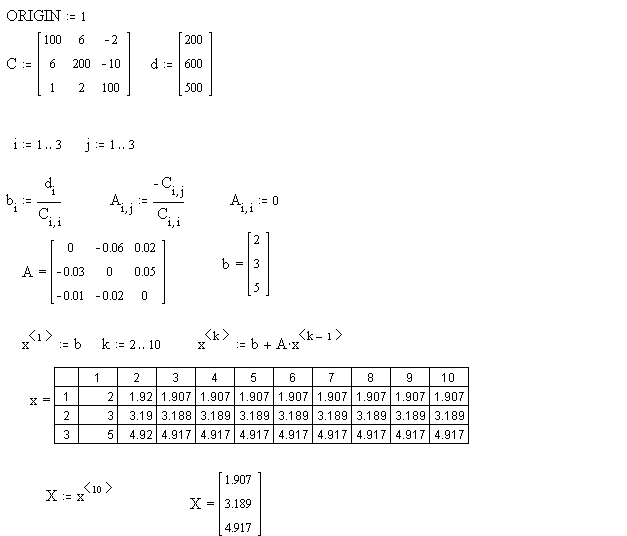
6.Решение системы линейных алгебраических уравнений методом Зейделя
Таблица 2
1. К какому типу - прямому или итерационному - относится метод Гаусса?
2. В чем заключается прямой и обратный ход в схеме единственного деления?
3. Как организуется, контроль над вычислениями в прямом и обратном ходе?
4. Как строится итерационная последовательность для нахождения решения системы линейных уравнений?
5. Как формулируется достаточные условия сходимости итерационного процесса?
6. Как эти условия связаны с выбором метрики пространства?
7. В чем отличие итерационного процесса метода Зейделя от аналогичного процесса метода простой итерации?
Лабораторная работа №3
Тема: Интерполирование функций
Пусть функция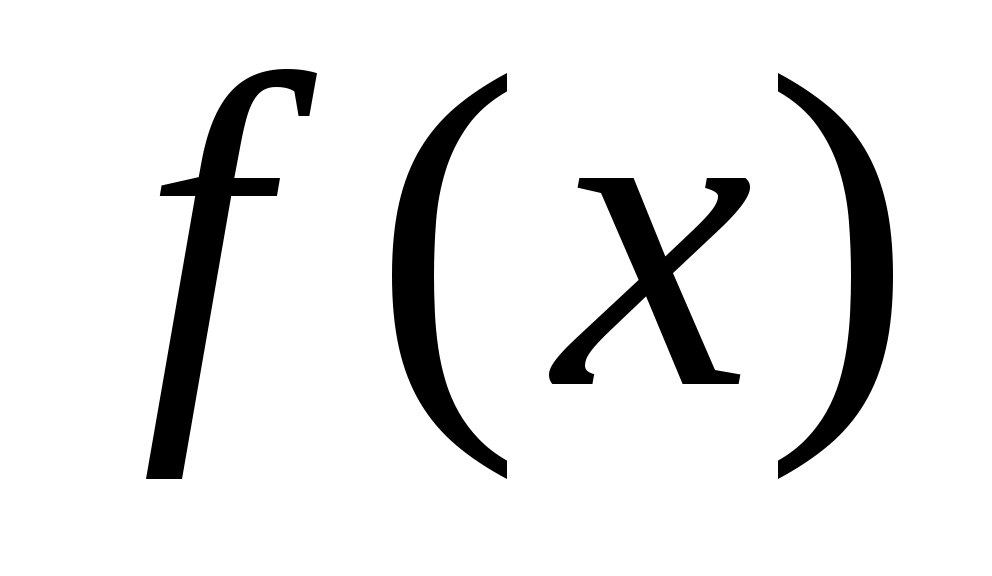 задана таблично, либо вычисление ее требует громоздких выкладок. Заменим приближенно функцию
задана таблично, либо вычисление ее требует громоздких выкладок. Заменим приближенно функцию 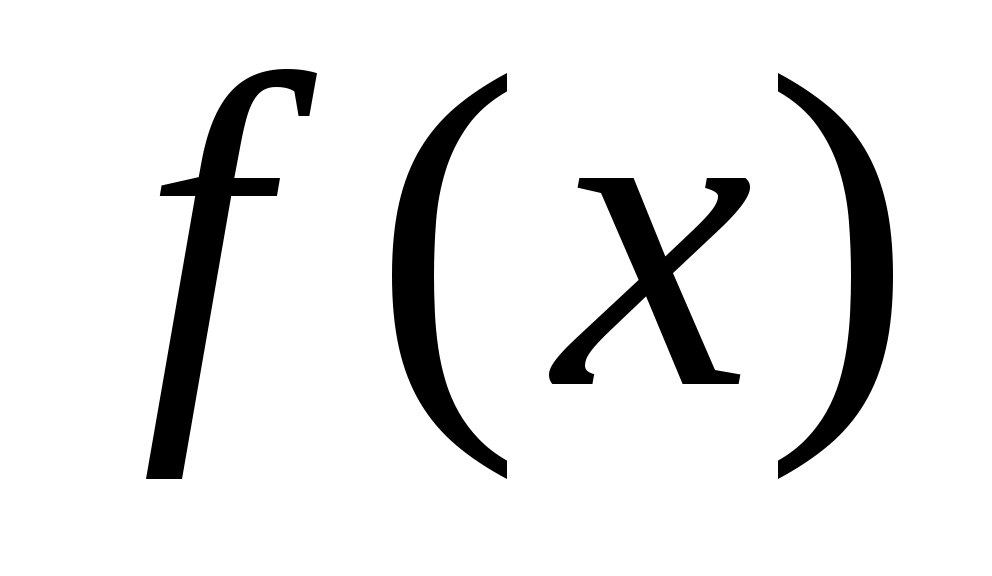 на какую-либо функцию
на какую-либо функцию 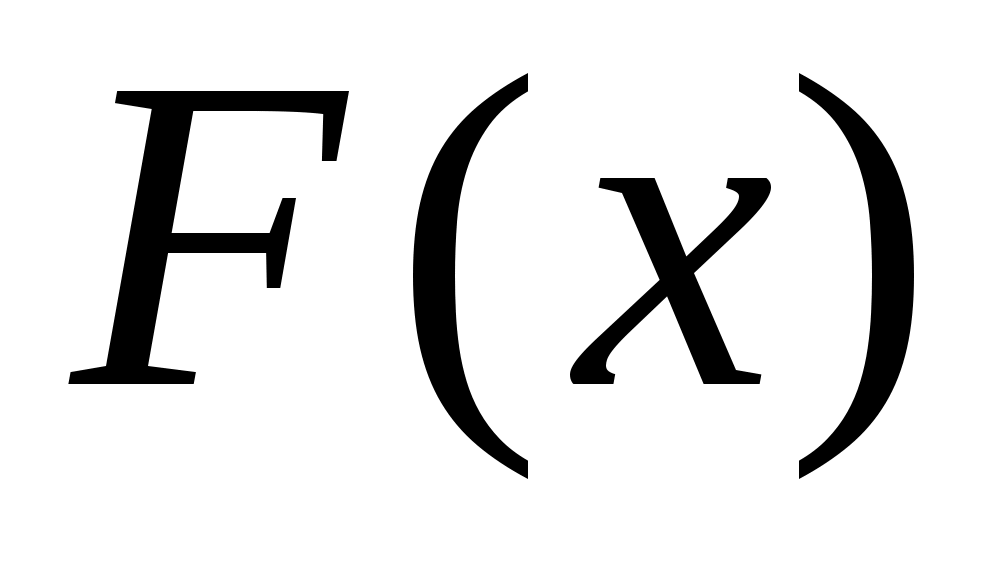 , так, чтобы отклонение
, так, чтобы отклонение 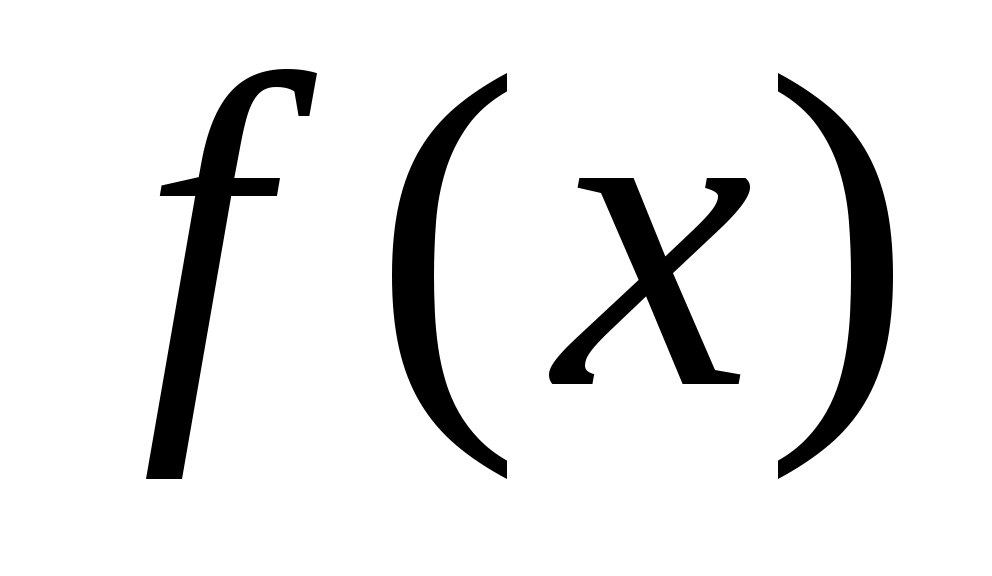 от
от 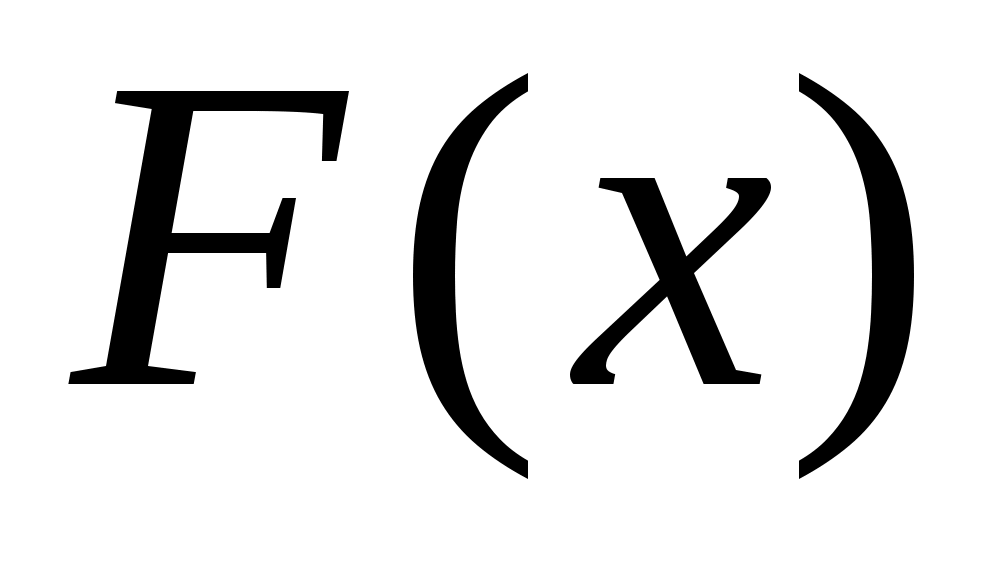 было в заданной области в некотором смысле минимальным. Подобная замена называется аппроксимацией функции
было в заданной области в некотором смысле минимальным. Подобная замена называется аппроксимацией функции 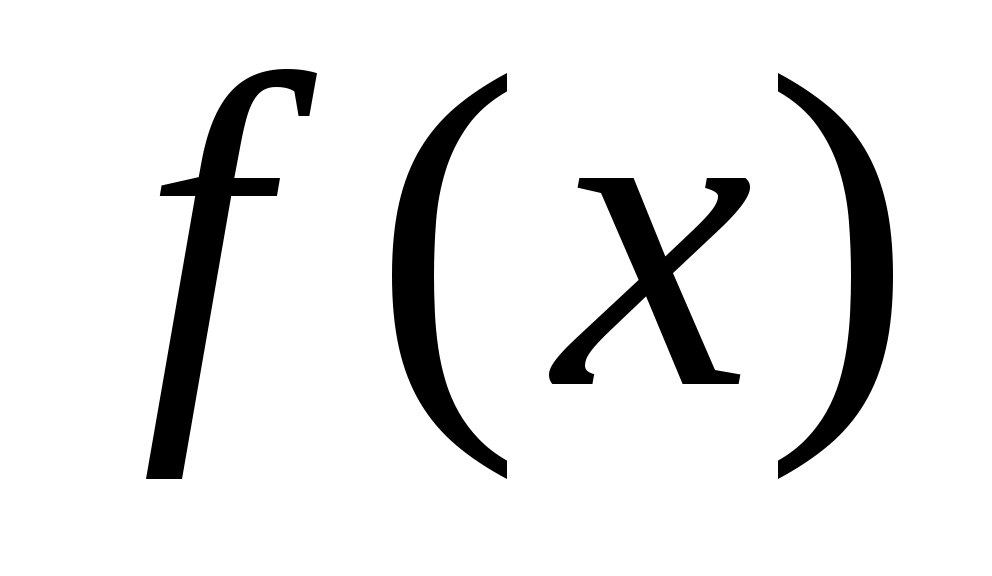 , а функция
, а функция 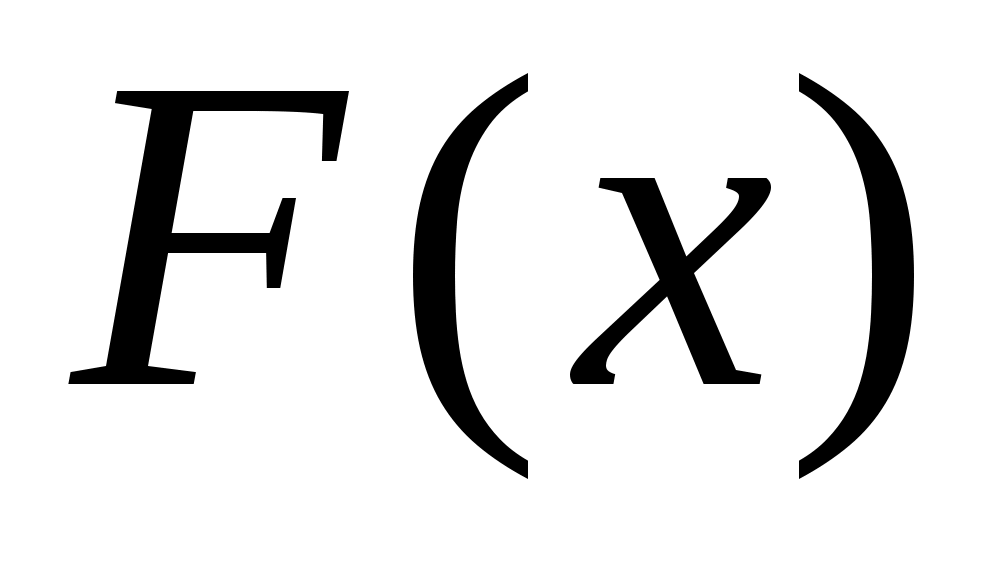 – аппроксимирующей (приближающей) функцией.
– аппроксимирующей (приближающей) функцией.
Классический подход к решению задачи построения приближающей функции основывается на требование строгого совпадения значений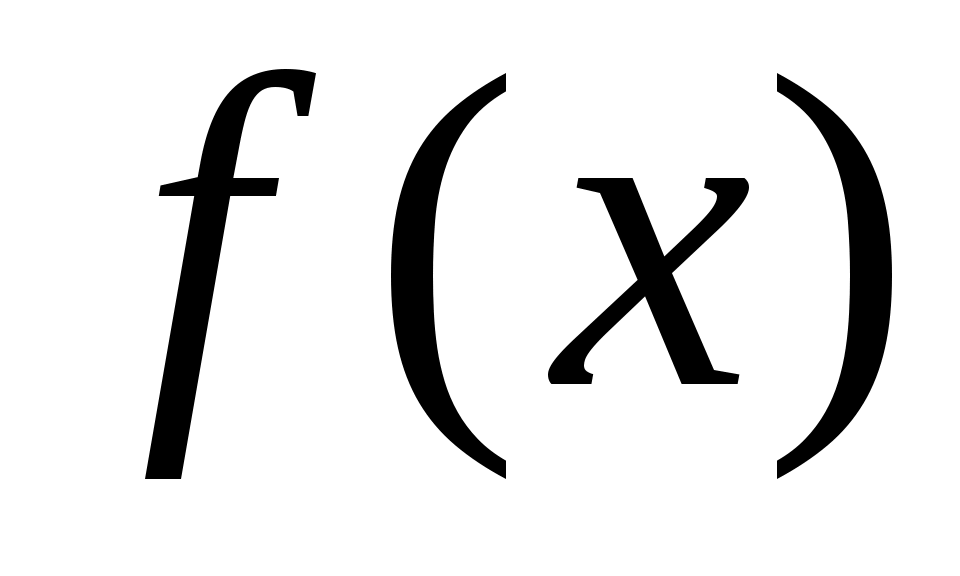 и
и 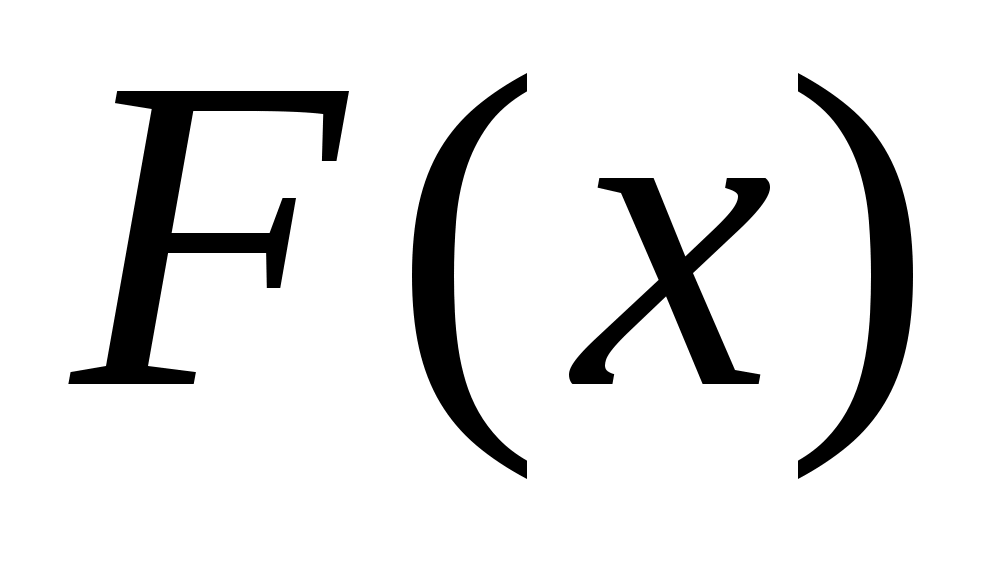 в точках
в точках 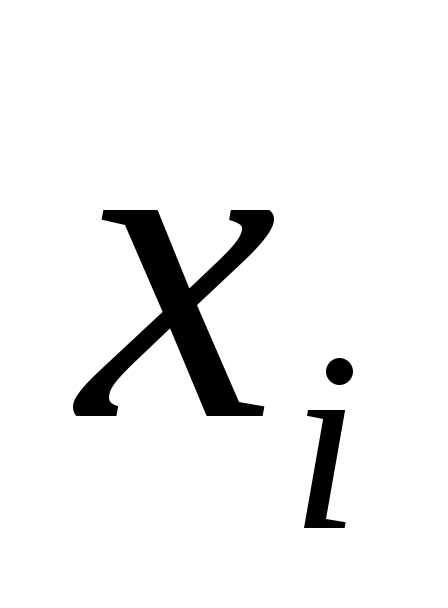 (
(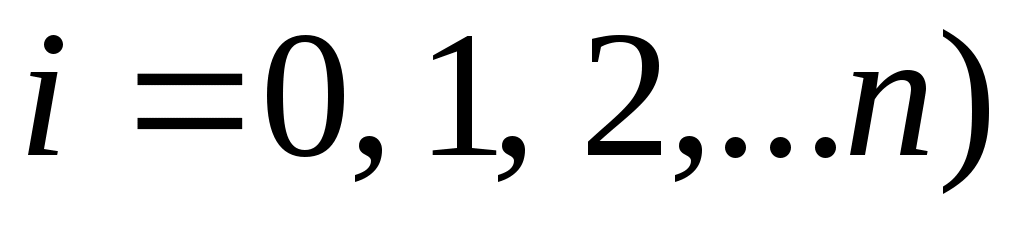 , т. е.
, т. е.
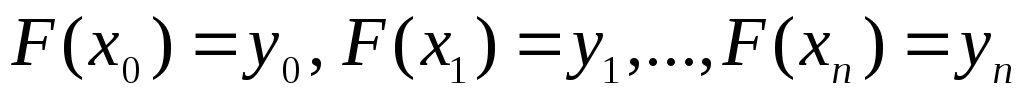 . (3.1)
. (3.1)
В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), точки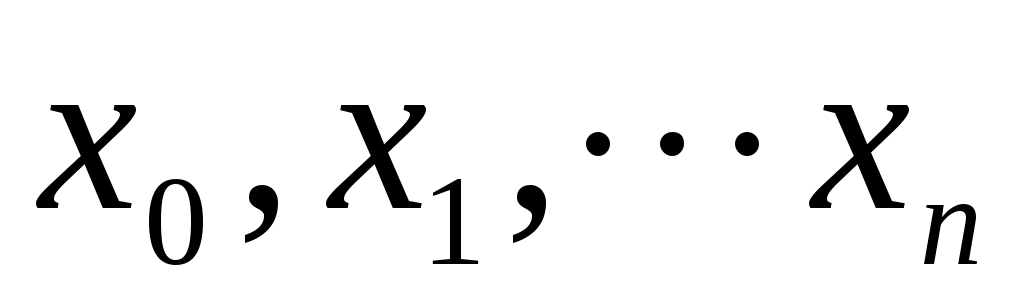
Предварительно приведем систему (2.2) к итерационному виду:
Для произвольного начального вектора
сходится, если выполнено одно из условий [2]
а)
б)
в)
Процесс вычислений заканчиваем при выполнении условия
где
Задание 3
Решить систему (2.1) методом Зейделя.
Метод Зейделя отличается от метода простой итерации тем, что найдя какое-то значение для компоненты, мы на следующем шаге используем его для отыскания следующей компоненты. Вычисления ведутся по формуле
Каждое из условий (2.4)-(2.6) является достаточным для сходимости итерационного процесса по методу Зейделя. Практически же удобнее следующее преобразование системы (2.2). Домножая обе части (2.2) на АТ, получим эквивалентную ей систему
где
Примерный вариант выполнения лабораторной работы
Пример. Решите систему уравнений
X1+2X2+3X3=7,
X1-3X2+2X3=5,
X1+X2+X3=3.
1. Символьное решение систем уравнений
Фрагмент рабочего документа с соответствующими вычислениями приведен ниже. Здесь = - логическое равенство.
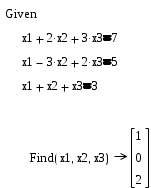
2. Решение системы линейных алгебраических уравнений как матричное уравнение Ax=b
Порядок выполнения задания.
-
Установите режим автоматических вычислений. -
Введите матрицу системы и матрицу-столбец правых частей. -
Вычислите решение системы по формуле x=A-1b. -
Проверьте правильность решения умножением матрицы системы на вектор-столбец решения. -
Найдите решение системы с помощью функции lsolve и сравните результаты.
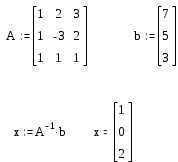
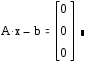
Решим систему с помощью функции lsolve и сравним результат с решением x=A-1b.
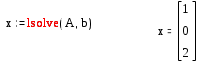
3. Решение линейной системы методом Гаусса
Комментарии. Функция augment(A,b) формирует расширенную матрицу системы добавлением к матрице системы справа столбца правых частей. Функция rrefприводит расширенную матрицу системы к ступенчатому виду, выполняя прямой и обратный ходы гауссова исключения. Последний столбец содержит решение системы.
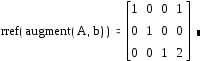
4. Решение системы методом Крамера
Порядок выполнения работы.
-
Вычисляем D определитель матрицы А. -
Зададим матрицу DX1, заменой первого столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX1. -
Зададим матрицу DX2, заменой второго столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX2. -
Зададим матрицу DX3, заменой третьего столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX3. -
Определяем решение системы линейных уравнений x1, x2, x3.
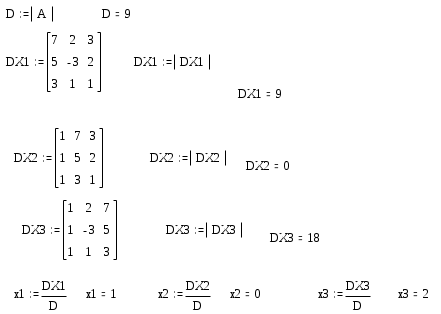
5.Решение системы линейных алгебраических уравнение методом простых итераций
Порядок выполнения задания
-
Введите матрицы C и d. -
Преобразуйте исходную систему Cx=d к виду x=b+Ax. -
Определите нулевое приближение решения. -
Задайте количество итераций. -
Вычислите последовательные приближения.
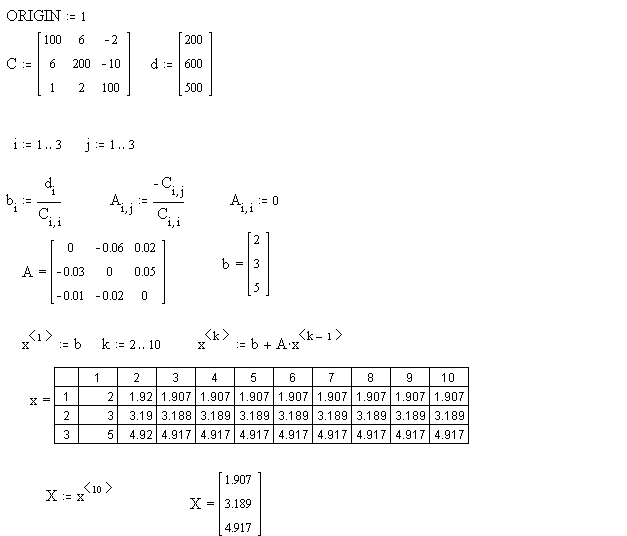
6.Решение системы линейных алгебраических уравнений методом Зейделя
Порядок выполнения задания
-
Введите матрицы С и d. -
Преобразуйте систему Cx=d к виду x=b+A1x+A2x. -
Определите нулевое приближение решения. -
Задайте количество итераций. -
Вычислите последовательные приближения.
Таблица 2
-
№
вар.
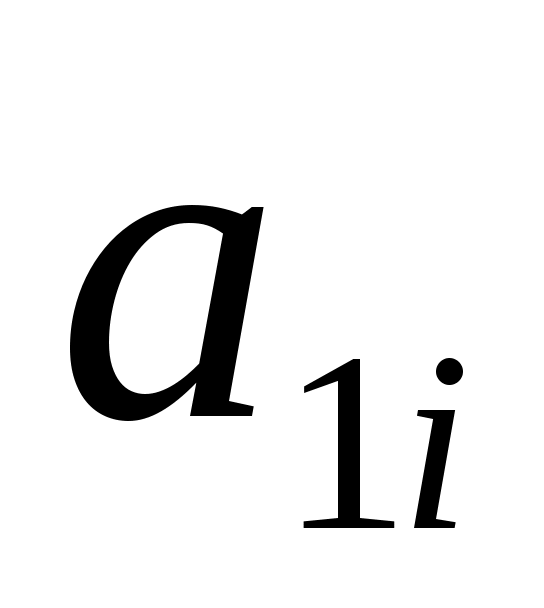
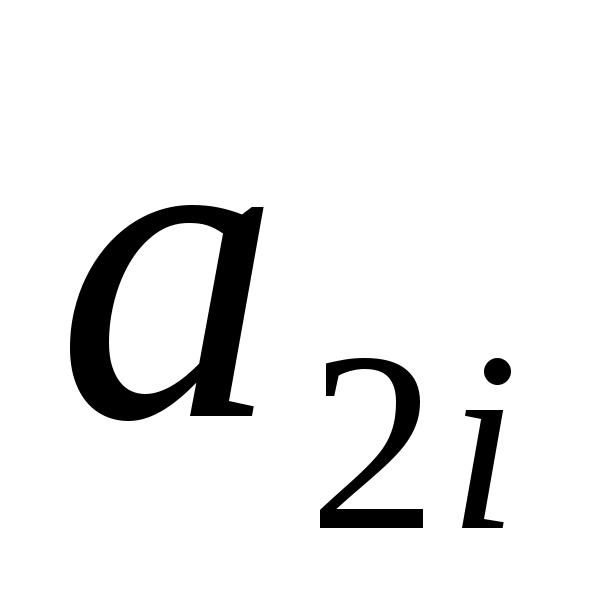
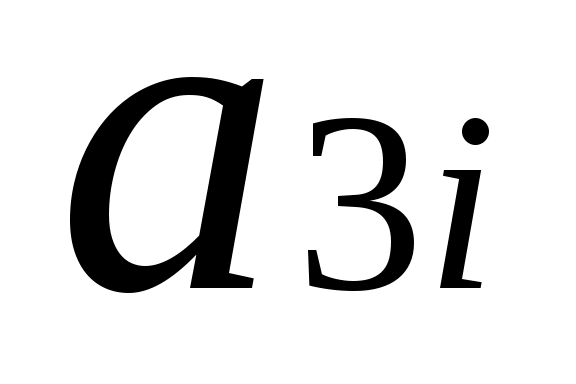
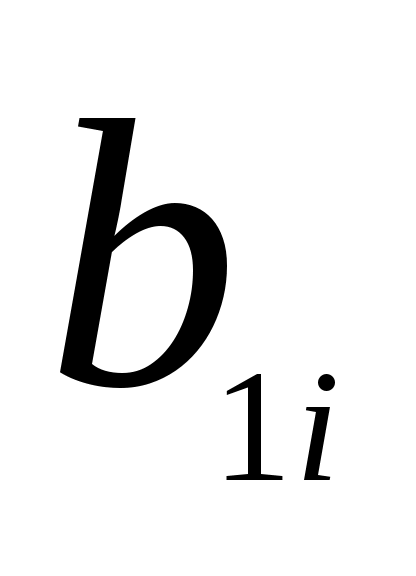
1
0.35
0.12
- 0.13
0.12
0.71
0.15
- 0.13
0.15
0.63
0.10
0.26
0.38
2
0.71
0.10
- 0.10
0.10
0.34
0.64
0.12
- 0.04
0.56
0.29
0.32
- 0.10
3
0.34
- 0.04
0.06
- 0.04
0.44
0.56
0.10
- 0.12
0.39
0.33
- 0.05
0.28
4
0.10
- 0.04
- 0.43
- 0.04
0.34
0.05
- 0.63
0.05
0.13
- 0.15
0.31
0.37
5
0.63
0.05
0.15
0.05
0.34
0.10
0.15
0.10
0.71
0.34
0.32
0.42
6
1.20
- 0.50
- 0.30
- 0.20
1.70
0.10
0.30
- 1.60
- 1.50
- 0.60
0.30
0.40
7
0.30
- 0.10
- 1.50
1.20
- 0.20
- 0.30
- 0.20
1.60
0.10
- 0.60
0.30
0.70
8
0.20
0.58
0.05
0.44
- 0.29
0.34
0.91
0.05
0.10
0.74
0.02
0.32
9
6.36
7.42
1.77
1.75
19.03
0.42
1.0
1.75
6.36
41.70
49.49
27.67
10
3.11
- 1.65
0.60
- 1.66
3.15
0.78
- 0.60
- 0.78
- 2.97
- 0.92
2.57
1.65
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. К какому типу - прямому или итерационному - относится метод Гаусса?
2. В чем заключается прямой и обратный ход в схеме единственного деления?
3. Как организуется, контроль над вычислениями в прямом и обратном ходе?
4. Как строится итерационная последовательность для нахождения решения системы линейных уравнений?
5. Как формулируется достаточные условия сходимости итерационного процесса?
6. Как эти условия связаны с выбором метрики пространства?
7. В чем отличие итерационного процесса метода Зейделя от аналогичного процесса метода простой итерации?
Лабораторная работа №3
Тема: Интерполирование функций
Пусть функция
Классический подход к решению задачи построения приближающей функции основывается на требование строгого совпадения значений
В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), точки