Файл: Руководство по выполнению лабораторных работ по предмету Вычислительная математика.doc

№					№ таблицы
1	0.65	0.80	0.05	0.01	3.6
2	0.25	0.40	0.05	0.025	3.5
3	0.75	0.90	0.05	0.01	3.6
4	0.70	0.85	0.05	0.025	3.6
5	0.80	0.95	0.05	0.025	3.6
6	0.1	0.25	0.05	0.025	3.5
7	0.15	0.3	0.05	0.025	3.5
8	0.7	0.85	0.05	0.025	3.6
9	0.2	0.35	0.05	0.01	3.5
10	0.80	0.95	0.05	0.01	3.6

Примерный фрагмент выполнения работы

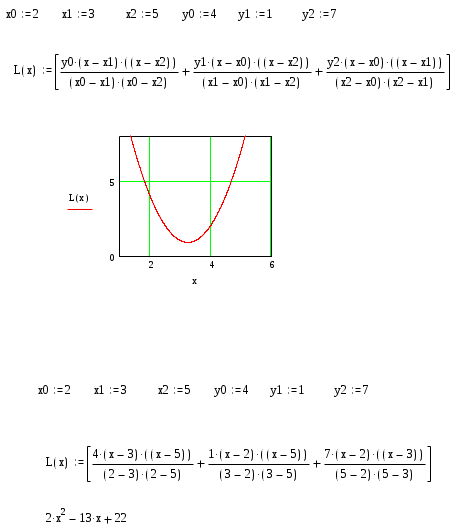
КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем особенность приближения таблично заданной функции методом интерполирования?

2. Как обосновывается существование и единственность интерполяционного многочлена?

3. Как связана степень интерполяционного многочлена с количеством узлов интерполяции?

4. Как строятся интерполяционные многочлены Лагранжа и Ньютона?

5. В чем особенности этих двух способов интерполяции?

6. Как производится оценка погрешности метода интерполяции многочленом Лагранжа?

7. Как используется метод интерполирования для уточнения таблиц функций?

8. В чем отличие между первой и второй интерполяционными формулами Ньютона?

Лабораторная работа №4

Тема: Численное интегрирование

Формулы, используемые для приближенного вычисления однократных интегралов, называют квадратурными формулами. Простой прием построения квадратурных формул состоит в том, что подынтегральная функция

заменяется на отрезке

интерполяционным многочленом, например, многочленом Лагранжа

; для интеграла имеем приближенное равенство (4.1). Предполагается, что отрезок

разбит на

частей точками (узлами)

, наличие которых подразумевается при построении многочлена

. Для равноотстоящих узлов



(4.1)

При определенных допущениях получаем формулу трапеций

(4.2)

где

 значения функции в узлах интерполяции.

Имеем следующую оценку погрешности метода интегрирования по формуле трапеций (4.2):

где

. (4.3)

Во многих случаях более точной оказывается формула Симпсона (формула парабол):

(4.4)

Для формулы Симпсона имеем следующую оценку погрешности:

где

.

Задание 1

Составить программу вычисления интеграла от заданной функции на отрезке

по формуле трапеций с шагом

. Сравнить результаты. Оценить точность по формуле (4.3). Сравнить результаты. Исходные данные для выполнения задания берутся из таблицы 4.

Задание 2

Составить программу вычисления интеграла от заданной функции на отрезке

по формуле Симпсона методом повторного счета с точностью

10^-6. Исходные данные для выполнения задания берутся из таблицы 4.
Примерный фрагмент выполнения лабораторной работы

Вычислить интеграл от заданной функции на отрезке [a,b] по формуле трапеций и прямым способом.

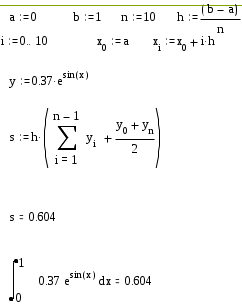
Таблица 4

N	Функция
1		0	1
2		1	2
3		1	2
4		2	3
5		0	1
6		1	2
7		1.2	2.2
8		1	2
9		2	3
10		3	4

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каковы преимущества формулы парабол по сравнению с формулой трапеций и следствием чего являются эти преимущества?

2. Верны ли формулы (4.2), (4.4) для неравноотстоящих узлов?

3. В каких случаях приближенные формулы трапеций и парабол оказываются точными?

4. Как влияет на точность численного интегрирования величина шага?

5. Каким способом можно прогнозировать примерную величину шага для достижения заданной точности интегрирования?

6. Можно ли добиться неограниченного уменьшения погрешности интегрирования путем последовательного уменьшения шага?
Лабораторная работа №5

Тема: Численное решение дифференциальных уравнений

Пусть дано дифференциальное уравнение первого порядка

. (5.1)

Требуется найти на отрезке

решение

, удовлетворяющее начальному условию

(5.2)

Будем предполагать, что условия теоремы существования и единственности выполнены. Для решения используем метод Эйлера (метод первого порядка точности, расчетные формулы (5.3)) и метод Рунге-Кутта (метод четвертого порядка точности, расчетные формулы (5.4)) с шагом h и 2h. Отметим, что результаты могут сильно отличаться, ввиду того, что метод Эйлера, имея только первый порядок точности, используется, как правило, для оценочных расчетов. Ориентировочную оценку погрешности метода Рунге-Кутта