Файл: Первый ввопрос.docx

Метод карт Карно

Карта Карно (минимизирующая карта) — это развертка некоторой объемной фигуры на плоскости. Карта Карно состоит из клеток, число которых равно числу наборов переменных функции. Каждая клетка соответствует строго определенному набору.

Например, карта Карно одной переменной (рис. 1.14): п = 1, число наборов N = 2" = 2.



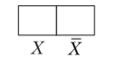
Рис. 1.14. Карта Карно одной переменной

Карта Карно двух переменных (рис. 1.15): п = 2, число наборов N=2² - 4.



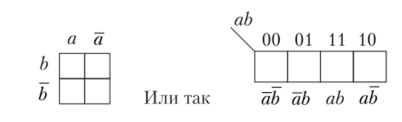
Рис. 1.15. Карта Карно двух переменных

Крайние клетки, соответствующие комбинациям 00 и 10, являются соседними и отличаются одной переменной а.

Переменные в карте могут располагаться произвольно, но любые соседние по вертикали ши по горизонтали клетки могут отличаться не более чем одной переменной.

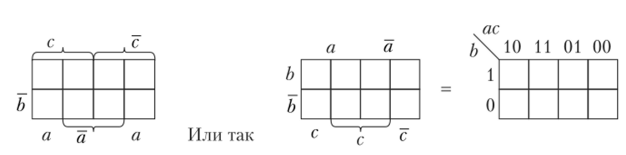
Карта Карно трех переменных (рис. 1.16): п = 3, число наборов Л^г = 2³ = 8.



Общие сведения и классификация

Счетчиком называют устройство, осуществляющее счет числа поданных на его вход импульсов и фиксирующее это число в двоичном коде. По направлению счета все счетчики делятся на суммирующие, вычитающие и реверсивные. В суммирующих счетчиках с приходом каждого импульса результат счета увеличивается на единицу. У вычитающих счетчиков каждый последующий импульс уменьшает число счета на единицу. Реверсивные счетчики могут производить подсчет импульсов как в режиме суммирования, так и в режиме вычитания.

Обычно счетчики строятся на Т-триггерах. С приходом каждого импульса происходит изменение состояния триггеров. По состоянию триггеров можно определить число поступивших на вход импульсов. Число триггеров в счетчике берется таким, чтобы множество их состояний превышало число импульсов, которое должно быть зафиксировано. Такое использование счетчика называют режимом счета. Если число импульсов не ограничено, то счетчик будет работать в режиме деления их числа на коэффициент счета К

---

_сч равный К_сч =2ⁿ, где n - число триггеров. Через каждые 2ⁿ импульсов он возвращается в начальное состояние и снова начинает счет.

Рассмотрим особенности каждого режима более детально.

Схема простейшего суммирующего счетчика на трех двухступенчатых Т-триггерах приведена на рис.1а, а условное графическое обозначение - на рис.1б.



 

 

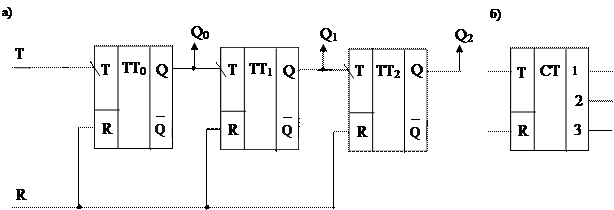
Рис.1

Входом счетчика является информационный вход триггера младшего разряда. Информационные входы последующих триггеров соединены с прямыми выходами предшествующих. Установочные входы триггеров объединены и образуют R-вход счетчика. Выходами счетчика являются прямые выходы триггеров.

Перед началом счета подается импульс на установочный вход R счетчика, который переводит все триггеры в состояние 0. Поскольку вход счетчика инверсный динамический, то в момент окончания первого импульса триггер Т₀ перейдет в состояние 1. Положительный перепад напряжения на его прямом выходе не изменит состояния Т₁ и Т₂, поэтому на выходах счетчика будет комбинация 001. После окончания второго импульса триггер Т₀ перейдет в состояние 0, а отрицательный перепад на его прямом выходе переведет триггер Т₁ в состояние 1. На выходах счетчика появится комбинация 010.

Порядок смены состояний счетчика наглядно отражают временные диаграммы (рис.2) и таблицы истинности (табл.1).

 

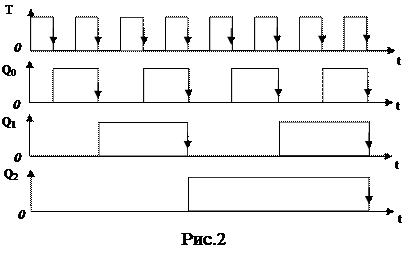 Таблица 1

номер инт.	Q2	Q1	Q0

---

 

Из таблицы и рисунка хорошо видно, что триггер младшего разряда меняет свое состояние с приходом каждого импульса, а триггер каждого последующего разряда - вдвое реже триггера предыдущего разряда. Рассмотренный счетчик осуществляет счет до К_сч=2³ - 1= 7. Для увеличения К_сч необходимо увеличить число триггеров. Рекомендуется в часы самоподготовки вычертить таблицу истинности суммирующего счетчика из четырех триггеров и определить коэффициент счета.

Вычитающий счетчик строится аналогичным образом. Отличие будет состоять в том, что информационный вход последующего триггера соединяется с инверсным выходом предыдущего, а для установки начального состояния будут использованы установочные входы S. Временные диаграммы и таблица истинности вычитающего счетчика приведены на рис.3 и в табл.2.

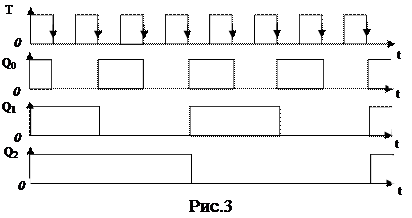 Таблица 2

номер инт.	Q2	Q1	Q0

Как видно из рисунка, начальное состояние триггеров - 1. Триггер младшего разряда также срабатывает по окончанию каждого импульса. Триггеры Т₁ и Т₂ изменяют свои состояния при положительном перепаде на входе счетчика, т.к. их входы соединены с инверсными выходами, где в этот момент генерируется отрицательный перепад.

Принцип построения реверсивных счетчиков поясняет рис.4.



 

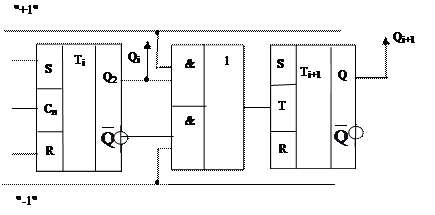
Рис.4

Реверсивный счетчик имеет один информационный вход -Т, два установочных S и R, и два управляющих "+1" и "-1".

---

Если счетчик используется как суммирующий, то для установки начального состояния используется вход R и на управляющий вход "+1" подается сигнал 1. Тогда информационный вход триггера Т_i+1 соединяется с прямым выходом триггера Т_i. При необходимости использовать тот же счетчик в режиме вычитания для установки начального состояния используется вход S и подается 1 на вход "-1". Тогда инверсный выход триггера Т_i соединяется с информационным входом триггера Т_i+1 .

Таким образом, счетчики, независимо от направления счета, с приходом каждого импульса меняют состояния триггеров. По изменению состояний триггеров можно определить число импульсов, поступивших на вход счетчика.

Сумматором называется комбинационное логическое устройство, предназначенное для выполнения операции арифметического сложения чисел, представленных в виде двоичных кодов.

Сумматоры являются одним из основных узлов арифметико-логического устройства. Термин сумматор охватывает широкий спектр устройств, начиная с простейших логических схем, до сложнейших цифровых узлов. Общим для всех этих устройств является арифметическое сложение чисел, представленных в двоичной форме. Рассмотрим более подробно некоторые конкретные схемотехнические решения, предназначенные для реализации поставленной задачи.

Классификация сумматоров может быть выполнена по различным признакам. Рассмотрим наиболее часто встречающиеся из них.



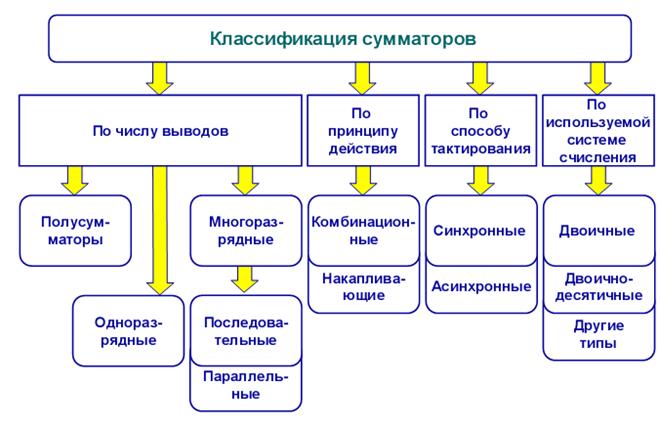
По числу выводов различают: полусумматоры, одноразрядные сумматоры, многоразрядные сумматоры.

Полусумматоромназывается устройство, предназначенное для сложения двух одноразрядных кодов, имеющее два входа и два выхода и формирующее из сигналов входных слагаемых сигналы суммы и переноса в старший разряд.

Однозаряднымсумматором называется устройство, предназначенное для сложения двух одноразрядных кодов, имеющее три входа и два выхода, и формирующее из сигналов входных слагаемых и сигнала переноса из младших разрядов сигналы суммы и переноса в старший разряд.

Многоразряднымсумматором называется устройство, предназначенное для сложения двух многоразрядных кодов, формирующее на выходе код суммы и сигнал переноса в случае, если результат сложения не может быть представлен кодом, разрядность которого совпадает с разрядностью кодов слагаемых.

---

В свою очередь, многоразрядные сумматоры подразделяются на последовательные и параллельные. В последовательных сумматорах операция сложения выполняется последовательно разряд за разрядом, начиная с младшего. В параллельных все разряды входных кодов суммируются одновременно.

Различают комбинационные сумматоры–устройства, не имеющие собственной памяти, и накапливающие сумматоры, снабженные собственной внутренней памятью, в которой аккумулируются результаты выполненной операции. При этом каждое очередное слагаемое прибавляется к уже имевшемуся в устройстве значению.

По способу тактирования различают синхронные и асинхронные сумматоры. В синхронныхсумматорах время выполнении операции арифметического суммирования двух кодов не зависит от вида самих кодов и всегда остается постоянным. В асинхроннных сумматорах время выполнения операции зависит от вида слагаемых. Поэтому по завершении выполнения суммирования необходимо вырабатывать специальный сигнал завершения операции.

В зависимости от используемой системы счисления различают двоичные, двоично-десятичные и другие типы сумматоров.

Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.

Сумматоры классифицируют по различным признакам.

В зависимости от системы счисления различают:

• 
  двоичные;
  
• 
  двоично-десятичные (в общем случае двоично-кодированные);
  
• 
  десятичные;
  
• 
  прочие (например, амплитудные).
  

По количеству одновременно обрабатываемых разрядов складываемых чисел:

• 
  одноразрядные,
  
• 
  многоразрядные.
  

По числу входов и выходов одноразрядных двоичных сумматоров:

• 
  четвертьсумматоры (элементы “сумма по модулю 2”; элементы “исключающее ИЛИ”), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
  
• 
  полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд);
  
• 
  полные одноразрядные двоичные сумматоры, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд).
  

---