Файл: 1. 1 Классификация, особенности, порядок проведения и приборы, используемые для съемки местности 4.docx
Добавлен: 06.11.2023
Просмотров: 547
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1 Классификация, особенности, порядок проведения и приборы, используемые для съемки местности
1.2 Создание сети съемочного обоснования
3 ОБРАБОТКА МАТЕРИАЛОВ ТЕОДОЛИТНОЙ СЪЕМКИ И ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОЛИГОНА.
3.1 Вычисление координат вершин точек замкнутого теодолитного хода
землеустройства – это вычисление площадей участков. В зависимости от формы, размера, требуемой точности площадь может быть вычислена аналитическим, графическим и механическим способом.
Аналитический способ определения площади заключается в вычислении площадей участков, ограниченных прямыми линиями, по результатам измерения длины линий и углов между ними на местности.
Площади участков с правильными с правильными геометрическими очертаниями вычисляют по формулам математики. Если участок имеет форму многоугольника, то его делят на простые геометрические фигуры, а общую площадь получают как сумму площадей этих фигур.
Если известны координаты границ углов поворота, то площадь вычисляют по координатам (1), (2):
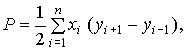(1)
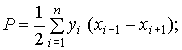………………………………………(2)
Графический способ определения площади заключается в их вычислении по измерениям, выполненным на плане с учетом масштаба. Если границы участка прямолинейны, то на плане их делят на простейшие фигуры, графически определяют длины линий, необходимых для вычисления площадей по выше приведенным формулам математики.Для контроля площадь каждой фигуры вычисляют дважды по разным сторонам.
Точность определения площадей зависит от точности измерения линии на плане и масштаба плана [4].
Расхождение между двумя значениями площади треугольника не должно превышать (3):
S=0,04M/10000*S, (3)
где
M – знаменатель масштаба плана,
S – площадь в га.
Палетка – сетка квадратов, со сторонами от 2 до 4 мм, изготовлена на прозрачном материале или сеть, параллельных линий, проведенных через 2 – 4 мм.
Палетку накладывают на контур и считают количество целых квадратов, а из нецелых, на глаз, составляют целые. Затем с учетом масштаба вычисляют площадь.
Механический способ заключается в определение площади участков с криволинейными границами с помощью планиметра.
Наиболее распространены полярные планиметры, состоящие из полюсного и обводного рычагов, соединенных шарниром и счетного механизма[4].
Делением планиметра называют 1/1000 окружности ободка счетного ролика.Цена деления планиметра - это количество площади в одном делении. Ее определяют, обводя квадрат с известной площадью, по формуле (4):
P=S/a – b, (4)
где
S – площадь квадрата,
a и b – отсчеты в начале и в конце обвода.
Площадь фигуры определяют, выполняя по два обвода и три отсчета, по которым вычисляют их разности. В обработку берут среднее, умножая его на цену деления. Точность определения площади планиметром порядка 1/400.
На точность определения площадей графическим
и механическим способами помимо перечисленных факторов влияет деформация бумаги, на которой опечатана карта [4,6].
Согласно требованиям, в документах кадастрового учета должна указываться точность определение площади.В настоящее время установление на местности границ объектов землеустройства выполняется с применением современных геодезических
приборов.
В процессе компьютерной обработки вычисляют координаты всех углов поворота границ и каждого здания на участке. Площадь получают автоматизировано по координатам.
Среднюю квадратическую ошибку "mp" определения площади участка прямоугольной формы полученную по координатам вычисляют по формуле (5):
mp=mtvp (5)
где
P – площадь участка,
K – коэффициент вытянутости – отношение длины участка к его ширине,
mp – средняя квадратическая ошибка положения межевого знака.
При геодезическом методе определения координат mt = 0.2 м. При картометрическом методе, когда координаты снимаются с планшетов масштаба 1:10000, mt= 2.5[4].
Обработка результатов полевых измерений в камеральных условиях в частности результатов в теодолитном ходу имеет следующую последовательность:
- уравнивание горизонтальных углов;
- вычисление дирекционных углов сторон теодолитного хода;
- вычисление приращений координат;
- уравнивание приращений координат;
- вычисление координат точек теодолитного хода.
Уравнивание горизонтальных углов включает в себя:
- вычисление угловой невязки хода и сравнение ее с допустимым значением;
- внесение поправок в измеренные значения горизонтальных углов;
- контроль вычислений[8,10].
Угловую невязку замкнутого теодолитного хода вычисляют по формуле (6):
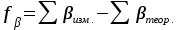, (6)
где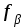
- угловая невязка хода;
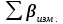- сумма измеренных горизонтальных углов;
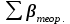- теоретическая сумма горизонтальных углов (истинное значение измеренной величины, в данном случае суммы углов).
Теоретическую сумму углов находят по известной в математике формуле суммы углов в многоугольнике 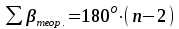(7):
, (7)
где n- количество вершин теодолитного хода.
Необходимо рассчитать допустимую угловую невязку по формуле (8):
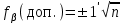. (9)
Угловая невязка хода не превышает допустимого значения. Выполнение данного условия дает право на вычисление поправки в измеренные горизонтальные углы. Вычисления производятся по формуле (10):
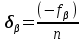
, (10)
где: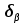
- поправка в измеренный горизонтальный угол;
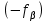- угловая невязка хода, взятая с «обратным знаком»;
n - количество вершин хода, на которых были измерены горизонтальные углы.
Для контроля вычисляют сумму вносимых поправок, она должна быть равна значению невязки, взятой с обратным знаком[8,10].
Внесение поправки и вычисление исправленных горизонтальных углов производится по формуле (11):
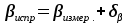. (12)
Для контроля вычисляют сумму исправленных горизонтальных углов и сравнивают ее с теоретическим значением. Суммы должны совпадать.
Вычисление дирекционных углов сторон теодолитного хода производится по формулам (6):
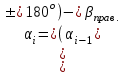(13)
где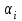
- дирекционный угол определяемой стороны;
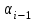- дирекционный угол исходной стороны (или предыдущей стороны теодолитного хода, дирекционный угол для которой уже вычислен);
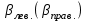- уравненные значения горизонтальных углов, левых или правых походу лежащих.
По правилам из зависимости между дирекционными угламии румбами (рис.2), производим расчет румбов[8,10].
Аналитический способ определения площади заключается в вычислении площадей участков, ограниченных прямыми линиями, по результатам измерения длины линий и углов между ними на местности.
Площади участков с правильными с правильными геометрическими очертаниями вычисляют по формулам математики. Если участок имеет форму многоугольника, то его делят на простые геометрические фигуры, а общую площадь получают как сумму площадей этих фигур.
Если известны координаты границ углов поворота, то площадь вычисляют по координатам (1), (2):
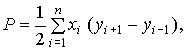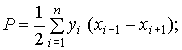(1) ………………………………………(2)Графический способ определения площади заключается в их вычислении по измерениям, выполненным на плане с учетом масштаба. Если границы участка прямолинейны, то на плане их делят на простейшие фигуры, графически определяют длины линий, необходимых для вычисления площадей по выше приведенным формулам математики.Для контроля площадь каждой фигуры вычисляют дважды по разным сторонам.
Точность определения площадей зависит от точности измерения линии на плане и масштаба плана [4].
Расхождение между двумя значениями площади треугольника не должно превышать (3):
S=0,04M/10000*S, (3)
где
M – знаменатель масштаба плана,
S – площадь в га.
Палетка – сетка квадратов, со сторонами от 2 до 4 мм, изготовлена на прозрачном материале или сеть, параллельных линий, проведенных через 2 – 4 мм.
Палетку накладывают на контур и считают количество целых квадратов, а из нецелых, на глаз, составляют целые. Затем с учетом масштаба вычисляют площадь.
Механический способ заключается в определение площади участков с криволинейными границами с помощью планиметра.
Наиболее распространены полярные планиметры, состоящие из полюсного и обводного рычагов, соединенных шарниром и счетного механизма[4].
Делением планиметра называют 1/1000 окружности ободка счетного ролика.Цена деления планиметра - это количество площади в одном делении. Ее определяют, обводя квадрат с известной площадью, по формуле (4):
P=S/a – b, (4)
где
S – площадь квадрата,
a и b – отсчеты в начале и в конце обвода.
Площадь фигуры определяют, выполняя по два обвода и три отсчета, по которым вычисляют их разности. В обработку берут среднее, умножая его на цену деления. Точность определения площади планиметром порядка 1/400.
На точность определения площадей графическим
и механическим способами помимо перечисленных факторов влияет деформация бумаги, на которой опечатана карта [4,6].
Согласно требованиям, в документах кадастрового учета должна указываться точность определение площади.В настоящее время установление на местности границ объектов землеустройства выполняется с применением современных геодезических
приборов.
В процессе компьютерной обработки вычисляют координаты всех углов поворота границ и каждого здания на участке. Площадь получают автоматизировано по координатам.
Среднюю квадратическую ошибку "mp" определения площади участка прямоугольной формы полученную по координатам вычисляют по формуле (5):
mp=mtvp (5)
где
P – площадь участка,
K – коэффициент вытянутости – отношение длины участка к его ширине,
mp – средняя квадратическая ошибка положения межевого знака.
При геодезическом методе определения координат mt = 0.2 м. При картометрическом методе, когда координаты снимаются с планшетов масштаба 1:10000, mt= 2.5[4].
3 ОБРАБОТКА МАТЕРИАЛОВ ТЕОДОЛИТНОЙ СЪЕМКИ И ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОЛИГОНА.
3.1 Вычисление координат вершин точек замкнутого теодолитного хода
Обработка результатов полевых измерений в камеральных условиях в частности результатов в теодолитном ходу имеет следующую последовательность:
- уравнивание горизонтальных углов;
- вычисление дирекционных углов сторон теодолитного хода;
- вычисление приращений координат;
- уравнивание приращений координат;
- вычисление координат точек теодолитного хода.
Уравнивание горизонтальных углов включает в себя:
- вычисление угловой невязки хода и сравнение ее с допустимым значением;
- внесение поправок в измеренные значения горизонтальных углов;
- контроль вычислений[8,10].
Угловую невязку замкнутого теодолитного хода вычисляют по формуле (6):
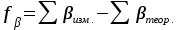, (6)где
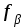- угловая невязка хода; 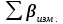- сумма измеренных горизонтальных углов; 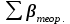- теоретическая сумма горизонтальных углов (истинное значение измеренной величины, в данном случае суммы углов).Теоретическую сумму углов находят по известной в математике формуле суммы углов в многоугольнике 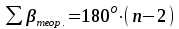(7):
, (7)где n- количество вершин теодолитного хода.
Необходимо рассчитать допустимую угловую невязку по формуле (8):
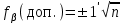. (9)Угловая невязка хода не превышает допустимого значения. Выполнение данного условия дает право на вычисление поправки в измеренные горизонтальные углы. Вычисления производятся по формуле (10):
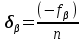
, (10)
где:
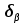- поправка в измеренный горизонтальный угол; 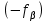- угловая невязка хода, взятая с «обратным знаком»;n - количество вершин хода, на которых были измерены горизонтальные углы.
Для контроля вычисляют сумму вносимых поправок, она должна быть равна значению невязки, взятой с обратным знаком[8,10].
Внесение поправки и вычисление исправленных горизонтальных углов производится по формуле (11):
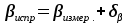. (12)Для контроля вычисляют сумму исправленных горизонтальных углов и сравнивают ее с теоретическим значением. Суммы должны совпадать.
Вычисление дирекционных углов сторон теодолитного хода производится по формулам (6):
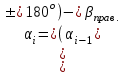(13)где
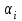- дирекционный угол определяемой стороны; 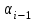- дирекционный угол исходной стороны (или предыдущей стороны теодолитного хода, дирекционный угол для которой уже вычислен); 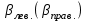- уравненные значения горизонтальных углов, левых или правых походу лежащих.По правилам из зависимости между дирекционными угламии румбами (рис.2), производим расчет румбов[8,10].
| Четверти | Значение α | Связь румбов с дирекционными углами | Знаки приращений координат | |
| | ∆x | ∆y | ||
| I-CВ | 00-900 | r=α | + | + |
| II-ЮВ | 900-1800 | r=1800-α | - | + |
| Ш-ЮЗ | 1800-2700 | r=α-1800 | - | - |
| IV-CЗ | 2700-3600 | r=3600-α | + | - |