Файл: Пояснительная записка к курсовой работе по дисциплине "Надежность информационных систем" кр 02068055. 230201. 09 042 пз.rtf

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 07.11.2023

Просмотров: 74

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Studlancer.net - закажи реферат, курсовую, диплом! Министерство образования и науки Российской ФедерацииФГБОУ ВПО "Брянская государственная инженерно – технологическая академия"Кафедра информационных технологийРасчет и повышение надежности информационной системыПояснительная записка к курсовой работепо дисциплине "Надежность информационных систем"КР – 02068055.230201.09 – 3.042 ПЗБрянск 2013 СодержаниеЗадание на курсовую работуВведение1. Первая часть. Кластерные вычислительные системы1.1 Классификация архитектур кластерных систем1.2 Топология кластеров1.3 Топология кластерных пар1.3.1 Топология N+11.3.2 Топология N×N1.3.3 Топология с полностью раздельным доступом2. Вторая часть2.1 Задание2.2 Исходные данные2.3 Декомпозиция схемыВывод по 2 части3. Задание3.1 РасчетВывод по 3 частиЗаключениеСписок используемой литературыЗадание на курсовую работуВ процессе выполнения курсовой работы необходимо: Ознакомиться с основными понятиями и методами расчета теории надежности. Рассмотреть и описать основные структурные схемы надежности. Получить навыки расчета базовых параметров системы (элемента), таких как вероятность безотказной работы, вероятность отказа, интенсивность отказов и др. В соответствии с заданием увеличить надежность рассматриваемых систем с помощью метода резервирования и метода повышения вероятности безотказной работы элементов. Для каждой из рассматриваемых задач построить графики зависимости вероятности безотказной работы элементов от времени, сделать выводы. ВведениеНадежность является фундаментальным понятием теории надежности, с помощью которого определяются другие понятия.Надежность – это свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих его способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования.Надежность является сложным свойством, и формируется такими составляющими, как безотказность, долговечность, восстанавливаемость и сохраняемость. Основным здесь является свойство безотказности – способность изделия непрерывно сохранять работоспособное состояние в течение времени. Потому наиболее важным в обеспечении надежности является повышение безотказности.Особенностью проблемы надежности является ее связь со всеми этапами "жизненного цикла" от зарождения идеи создания до списания: при расчете и проектировании изделия его надежность закладывается в проект, при изготовлении надежность обеспечивается, при эксплуатации – реализуется.Поэтому проблема надежности – комплексная проблема и решать ее необходимо на всех этапах и разными средствами. На этапе проектирования изделия определяется его структура, производится выбор или разработка элементной базы, поэтому здесь имеются наибольшие возможности обеспечения требуемого уровня надежности.Основным методом решения этой задачи являются расчеты надежности (в первую очередь – безотказности), в зависимости от структуры объекта и характеристик его составляющих частей, с последующей необходимой коррекцией проекта. В результате расчета определяются количественные значения показателей надёжности.1. Первая часть. Кластерные вычислительные системыОдно из самых современных направлений в области создания вычислительных систем – это кластеризация. По производительности и коэффициенту готовности кластеризация представляет собой альтернативу симметричным мультипроцессорным системам. Понятие "кластер" можно определить как группу взаимно соединенных вычислительных систем (узлов), работающих совместно как единый вычислительный ресурс и создающих иллюзию наличия единственной ВМ. В качестве узла кластера может выступать как однопроцессорная ВМ, так и ВС типа SMP или MPP. Важно лишь то, что каждый узел может использоваться самостоятельно и отдельно от кластера. В плане архитектуры суть кластерных вычислений сводится к объединению нескольких узлов высокоскоростной сетью. Для описания такого подхода, помимо термина кластерные вычисления, достаточно часто применяют такие термины, как: "кластер рабочих станций" (workstation cluster), "гипервычисления" (hypercomputing), "параллельные вычисления на базе сети" (network-based concurrent computing), "ультравычисления" (ultracomputing).Изначально перед кластерами ставились две задачи: достичь большой вычислительной мощности и обеспечить повышенную надежность ВС. Пионером в области кластерных архитектур считается корпорация DEC, создавшая первый коммерческий кластер в начале 80-х годов прошлого века.В качестве узлов кластеров могут использоваться как одинаковые ВС (гомогенные кластеры), так и разные (гетерогенные кластеры). По своей архитектуре кластерная ВС является слабосвязанной системой.В работе [BREW97] перечисляются четыре преимущества, достигаемые с помощью кластеризации: абсолютная масштабируемость. Возможно создание больших кластеров, превосходящих по вычислительной мощности даже самые производительные одиночные ВМ. Кластер может содержать десятки узлов, каждый из которых представляет собой мультипроцессор; наращиваемая масштабируемость. Кластер строится так, что его можно наращивать, добавляя новые узлы небольшими порциями. Таким образом, пользователь может начать с умеренной системы, расширяя ее по мере необходимости; высокий коэффициент готовности. Поскольку каждый узел кластера – самостоятельная ВМ или ВС, отказ одного из узлов не приводит к потере работоспособности кластера. Во многих системах отказоустойчивость автоматически поддерживается программным обеспечением; Превосходное соотношение цена/производительность. Кластеры любой производительности можно создать, используя стандартные "строительные блоки", при этом стоимость кластера будет ниже, чем у одиночной ВМ с эквивалентной вычислительной мощностью. На уровне аппаратного обеспечения кластер – это просто совокупность независимых вычислительных систем, объединенных сетью. При соединении машин в кластер почти всегда поддерживаются прямые межмашинные связи. Решения могут быть простыми, основывающимися на аппаратуре Ethernet, или сложными с высокоскоростными сетями с пропускной способностью в сотни мегабайт в секунду. К последней категории относятся RS/6000 SP фирмы IBM, системы фирмы Digital на основе Memory Channel, ServerNet фирмы Compac Computer Corp.Узлы кластера контролируют работоспособность друг друга и обмениваются специфической кластерной информацией. Контроль работоспособности осуществляется с помощью специального сигнала, часто называемого heartbeat, что можно перевести как сердцебиение. Этот сигнал передается узлами кластера друг другу чтобы подтвердить их нормальное функционирование.Неотъемлемая часть кластера – специализированное программное (ПО) обеспечение, на которое возлагается задача поддержания вычислений при отказе одного или нескольких узлов. Такое ПО производит перераспределение вычислительной нагрузки при отказе одного или нескольких узлов кластера, а также восстановление вычислений при сбое в узле. Кроме того, при наличии в кластере совместно используемых дисков, кластерное ПО поддерживает единую файловую систему. 1.1 Классификация архитектур кластерных систем В литературе приводятся различные способы классификации кластеров. Так, простейшая классификация ориентируется на то, являются ли диски в кластере совместно используемыми всеми узлами. На рис. 1, а показан кластер из двух узлов, координация работы которых обеспечивается за счет высокоскоростной линии, используемой для обмена сообщениями. Такой линией может быть локальная сеть, используемая также и не входящими в кластер компьютерами, либо выделенная линия. В последнем случае один или несколько узлов кластера будут иметь выход на локальную или глобальную сеть, благодаря чему обеспечивается связь между серверным кластером и удаленными клиентскими системами. Рисунок 1 – Конфигурации кластеров: а – без совместно используемых дисков; б – с совместно используемыми дискамиБолее ясную картину дает классификация кластеров по их функциональным особенностям. Такая классификация приведена в таблице 1.Таблица 1 – Методы кластеризации

1.2 Топология кластеров

1.3 Топология кластерных пар

2.1 Задание

2.2 Исходные данные

2.3 Декомпозиция схемы

2.4 Вывод по 2 части

3.1 Задание

3.2 Расчет

3.3 Вывод по 3 части



3. Обеспечить увеличение γ – процентной наработки не менее чем в 1.5 раза за счет:

а) повышения надежности элементов;

б) структурного резервирования элементов системы.

Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.


2.2 Исходные данные





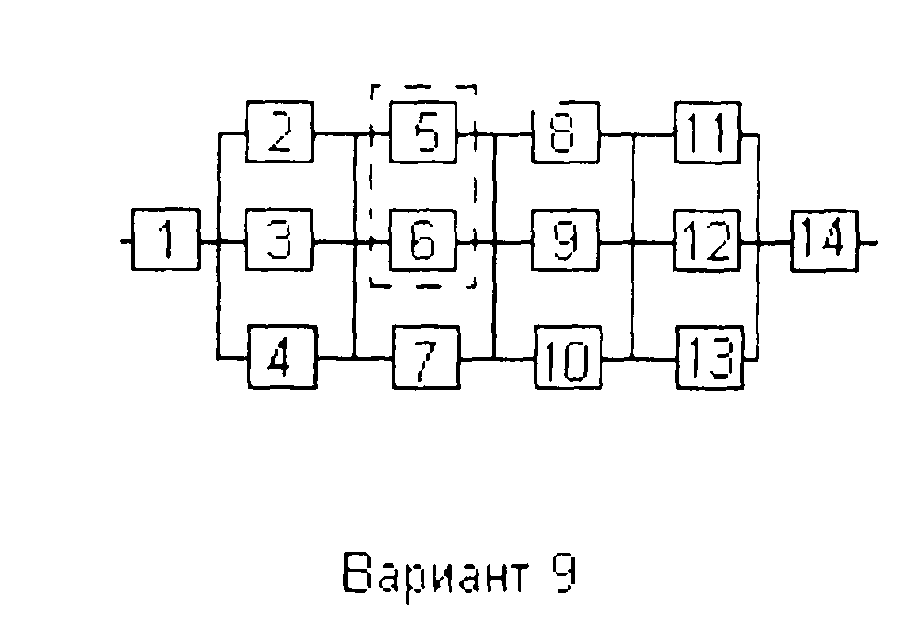
Рисунок 6 – Структурная схема надежности

g,
Интенсивности отказов элементов, l i, x10-6 1/ч

%
1
2
3
4
5
6
7
8
9
10
11
12
13
14

60
0.03
0.5
0.2
1.0
0.03
0.1


2.3 Декомпозиция схемы



Преобразуем следующие параллельные элементы:

Элементы 2 и 3, 4 в исходной схеме заменим квазиэлементом A, учитывая, что p2=p3=p4 получим:
PA = 1 – Q2 * Q2 * Q3 * Q4 = 1 – (1 - P2)3
Элементы 5, 6 и 7 образуют соединение "2 из 3". Так как P5 = P6 = P7, то для определения вероятности безотказной работы элемента F воспользуемся комбинаторным методом:

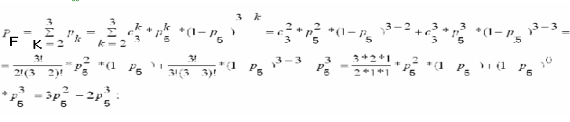
В исходной схеме элементы 8, 9 и 10 образуют параллельное соединение. Заменяем их квазиэлементом С. Учитывая, что p8 = p9=p10, получим:
PС = 1 – (1 – P8)3
В исходной схеме элементы 11 и 12 и 13 образуют параллельное соединение. Заменяем их квазиэлементом D. Учитывая, что p8 = p9=p10, получим:
PD
= 1 – (1 – P11)3
Преобразованная схема изображена на рисунке 7.


Рисунок 7 – Преобразованная схема системы
Элементы А, F, С, D (рис. 2) образуют мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом минимальных путей. Таким образом, вероятность работы квазиэлемента G можно определить по формуле:
PG=1-(1- PA * PF * PС * PD)
Преобразованная схема изображена на рисунке 8.


Рисунок 8 – Преобразованная схема системы
В преобразованной схеме (рис. 8) элементы 1, G, и 14 образуют последовательное соединение. Тогда вероятность безотказной работы всей системы определяется выражением:

Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 14 подчиняются экспоненциальному закону:


Результаты расчетов вероятностей безотказной работы элементов 1 – 14 исходной схемы по формуле для наработки до 3·106 часов представлены в таблице.

Результаты расчетов вероятностей безотказной работы квазиэлементов А, В, С, D, F и G также представлены в таблице.

На рисунке 9 представлен график зависимости вероятности безотказной работы системы Р от времени (наработки) t.

По графику (кривая Р) находим для γ = 60% (Р = 0.6) γ-процентную наработку системы t = 0.93•106 ч.

Проверочный расчет при t = 0.93•106 ч показывает, что Pγ = 0,5921 0,6.

По условиям задания находим время, превышающее в 1,5 раза время, соответствующее вероятности безотказной работы, равное 0,6 (Pγ = 0,6):
.
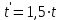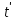= 1,5·0,93·106 = 1.425·106 ч.

Расчет показывает, что при t =1.425106 ч для элементов преобразованной схемы p1=0.9582, pG = 0.4124, p14= 0.8672. Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент G и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.

Для того, чтобы = 1.425106 ч система в целом имела вероятность безотказной работы Рg =0.6, необходимо, чтобы элемент G имел вероятность безотказной работы.

PG=Py/(P1*P14)=0.6/(0.9582*0.8672)=0.722
При этом значении элемент G останется самым ненадежным в схеме.

Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями, более целесообразно использовать графоаналитический метод. для этого строим график зависимости PG =f (p12)


Рисунок 9 – График зависимости вероятности безотказной работы системы Р от времени (наработки) t.


элементы

λ1, 10-6
Наработка t, 106



0,5
1
1,5
2
2,5
3
0,95
1,425

1,11-13
0,03
0,9851
0,9704
0,9560
0,9418
0,9277
0,9139
0,9719
0,9582

2-4
0,5
0,7788
0,6065
0,4724
0,3679
0,2865
0,2231
0,6219
0,4904

5-7
0,2
0,9048
0,8187
0,7408
0,6703
0,6065
0,5488
0,8270
0,7520

8-10
1
0,6065
0,3679
0,2231
0,1353
0,0821
0,0498
0,3867
0,2405

14
0,1
0,9512
0,9048
0,8607
0,8187
0,7788
0,7408
0,9094
0,8672

A


0,9892
0,9391
0,8531
0,7474
0,6368
0,5311
0,9459
0,8677

C


0,9391
0,7474
0,5311
0,3535
0,2266
0,1420
0,7694
0,5619

D


1,0000
1,0000
0,9999
0,9998
0,9996
0,9994
1,0000
0,9999

F



0,9746
0,9133
0,8333
0,7456
0,6574
0,5730
0,9205
0,8460

G


0,9053
0,6410
0,3775
0,1970
0,0948
0,0432
0,6699
0,4124

P


0,8483
0,5629
0,3107
0,1519
0,0685
0,0293
0,5921
0,3427

1',11'-13'
0,0106
0,9947
0,9895
0,9842
0,9790
0,9738
0,9687
0,9900
0,9850

D'


1,0000
0,9999
0,9999
0,9999
0,9999
0,99996
0,999999
0,999997

G'


0,9053
0,6411
0,3776
0,1970
0,0949
0,0432
0,6699
0,4125

P'


0,8566
0,5739
0,3199
0,1579
0,0719
0,0310
0,6031
0,3523



Рисунок 10 – График зависимости PG =f (p12).
По графику при pG = 0.722 находим p120,985

Тогда
λ11,12,13= 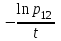=0,01064×106

2.4 Вывод по 2 части



В результате проделанной работы мы можем сделать вывод, что повышение надежности элементов не всегда представляется возможным.

Выбранная и спроектированная нами система удовлетворяет всем поставленным требованиям.

3. Третья часть


3.1 Задание



Сформировать структурную схему для расчета надежности информационной системы закупочного предприятия "книжный магазин". Задать значения интенсивности отказа для каждого элемента структурной схемы. По структурной схеме надежности ИС и заданным значениям интенсивности отказа ее элементов определить вероятность безотказной работы данной схемы.


Рисунок 11 – Исходная схема
Элементы 1 и 2 – автоматизированные рабочие места склада №1 и №2

Элементы 3,4,5 – автоматизированные рабочие места менеджера.

6 и 7 – кассы №1 и №2

Элемент 8 – печать (принтер).

Значения интенсивности отказа элементов составляют:

λ1 = λ2 = 0,03*10-6 1/ч;

λ3 = λ4 =λ5 =2,0*10-6 1/ч;

λ6 = λ7 = 0,12*10-6 1/ч;

λ8 = 4,0*10-6 1/ч

Все элементы системы работают в режиме нормальной эксплуатации.

Необходимо рассчитать вероятность безотказной работы системы в зависимости от времени наработки.

3.2 Расчет



1. В исходной схеме элементы 1 и 2 образуют параллельное соединение.

Заменяем их квазиэлементом A. Учитывая, что p1=p2 получим:

2. Элементы 3, 4 и 5 также образуют параллельное соединение, заменив которое элементом B и учитывая, что p3=p4=p5 получим:

3. Элементы 6 и 7 также образуют параллельное соединение, заменив которое элементом C и учитывая, что p6=p7 получим:

4. После преобразования схема примет вид, изображенный на рис. 14.


Рисунок 12 – Преобразованная схема
5. В преобразованной схеме (рис. 14) элементы A, B, C и 8 образуют последовательное соединение. Тогда вероятность безотказной работы всей системы определяется выражением:

6. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 8 (рис. 13) подчиняется экспоненциальному закону:

7. Результаты расчетов вероятности безотказной работы элементов 1 – 8 исходной схемы для наработки до 106 часов представлены в табл. 1.
Таблица 1 – Расчет вероятности безотказной работы

Элемент
l i, x10-6 1/ч
Наработка t, x 106 ч

0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1

1,2
1
0,9048
0,8187
0,7408
0,6703
0,6065
0,5488
0,4966
0,4493
0,4066
0,3679

3,4,5
2
0,8187
0,6703
0,5488
0,4493
0,3679
0,3012
0,2466
0,2019
0,1653
0,1353

6,7
0,5
0,9512
0,9048
0,8607
0,8187
0,7788
0,7408
0,7047
0,6703
0,6376
0,6065

8
3
0,7408
0,5488
0,4066
0,3012
0,2231
0,1653
0,1225
0,0907
0,0672
0,0498

A
-
0,9909
0,9671
0,9328
0,8913
0,8452
0,7964
0,7466
0,6968
0,6478
0,6004

B
-
0,9671
0,8913
0,7964
0,6968
0,6004
0,5117
0,4324
0,3630
0,3033
0,2524

C
-
0,9976
0,9909
0,9806
0,9671
0,9511
0,9328
0,9128
0,8913
0,8687
0,8452

P
-
0,7083
0,4688
0,2962
0,1809
0,1077
0,0628
0,0361
0,0205
0,0115
0,0064

Смотрите также файлы