Файл: Задача 2 4 Задача 3 8 Задания по теме Статистическая группировка, вторичная перегруппировка.docx
Добавлен: 07.11.2023
Просмотров: 127
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 1
Для обеих таблиц:
Рассчитать (для любой из подгрупп):
- все виды относительных величин (по 2 варианта на каждую доступную для расчета величину);
- все виды средних величии (в том числе способов моментов);
- все показатели вариации.
Проинтерпретировать все полученные результаты.
Для группировки в табл. 8 рассчитаем относительные величины структуры в табл. 9
Таблица 9 – Относительные величины структуры
| Количество компьютеров в офисе компании | Число офисов | Структура, % |
| 2 | 15 | 15/250= 6 |
| 3 | 38 | 15,2 |
| 4 | 55 | 22 |
| 5 | 112 | 44,8 |
| 6 и более | 30 | 12 |
| ИТОГО: | 250 | 100 |
Расчеты показали, что наибольшее число офисов 112 имеют по 5 компьютеров и занимаю 44,8% б общей численности выборки офисов.
Определим относительные величины структуры для табл. 7 и берем возраст родителей 18-22 лет.
Таблица 10- структура семей по количеству детей
| Возраст вступления в брак, кол-во лет / количество детей в родительской семье | 1 | 2 | 3 и более | Итого: |
| 18-22 | 15 | 25 | 18 | 58 |
| Структура, % | 15/58= 25,86 | 43,1 | 31,04 | 100 |
Определим относительные показатели динамики. За 1 примем семьи с 1 ребенком.
Таблица 10- Динамика численности детей в семье
| Возраст вступления в брак, кол-во лет / количество детей в родительской семье | 1 | 2 | 3 и более | Итого: |
| 18-22 | 15 | 25 | 18 | 58 |
| Относительные показатели динамики | 1 | 25\15= 1.67 | 18/15= 1,2 | - |
Расчеты показали, что у родителей, которые вступили в брак в возрасте 18-22 года в 43,1% в семье 2 ребенка
Определим средние величины по формуле:
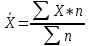
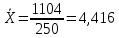
Таблица 11 – Расчетная
| Количество компьютеров в офисе компании | Число офисов | п*х | 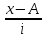 | Х-А | 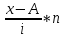 | 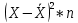 |
| 2 | 15 | 30 | -2 | -2 | -30 | 87,56 |
| 3 | 38 | 114 | -1 | -1 | -38 | 76,19 |
| 4 | 55 | 220 | 0 | 0 | 0 | 9,52 |
| 5 | 112 | 560 | 1 | 1 | 112 | 38,20 |
| 6 и более | 30 | 180 | 2 | 2 | 60 | 75,27 |
| ИТОГО: | 250 | 1104 | 0 | 0 | 104 | 286,74 |
Определим среднее значение методом моментов:
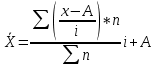
А = 4
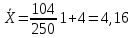
Определим дисперсию по формуле:
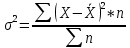
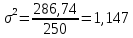
Определим среднеквадратическое отклонение:
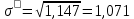
Определим коэффициент вариации:
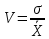
V = 1,071/4,416= 0,2425 или 24,25%
Расчеты показали, что в среднем в офисе находится 4,4 компьютеров
Коэффициент вариации показывает, что совокупность достаточно однородная.
Аналогично проводим расчеты и по семьям
Таблица 12 – Расчетная
| Возраст вступления в брак, кол-во лет | Число семей с 1 ребенком | Х | п*х |  |
| до 18 | 9 | 17 | 153 | 537,776 |
| 18-22 | 15 | 20 | 300 | 335,594 |
| 22-25 | 43 | 23,5 | 1010,5 | 65,055 |
| 25-27 | 36 | 26 | 936 | 58,064 |
| 27 и старше | 12 | 37 | 444 | 1806,635 |
| ИТОГО: | 115 | | 2843,5 | 2803,124 |
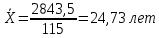
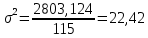
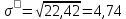
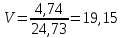
Средний возраст родителей, при вступлении в барк, которые имеют в семье 1 ребенка составляет 24,7 лет. Методом моментов нельзя рассчитать т.к. интервалы не одинаковые.
Коэффициент вариации показывает, что совокупность достаточно однородная.
Задача 2
Построить моду и медиану графически (выбрать любую подгруппу, кроме той, по которой производились расчеты в задании 1).
Решение
Составим расчетную таблицу
Таблица 12 – Расчетная
| Возраст вступления в брак, | Число семей с 2 ребенка | Х | ст-ра, % | кумулятива,% |
| кол-во лет | ||||
| до 18 | 15 | 17 | 15/135= 11,11% | 11,11% |
| 18-22 | 25 | 20 | 18,52% | 29,63% |
| 22-25 | 51 | 23,5 | 37,78% | 67,41% |
| 25-27 | 34 | 26 | 25,19% | 92,59% |
| 27 и старше | 10 | 37 | 7,41% | 100,00% |
| ИТОГО: | 135 | | 100 | |
На рис. 6 представим определение моды, а на рис. 7 – медиана
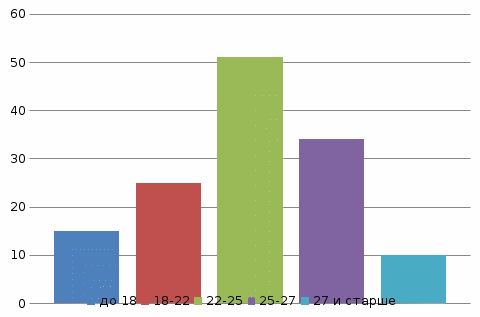
Рисунок 6 - Мода
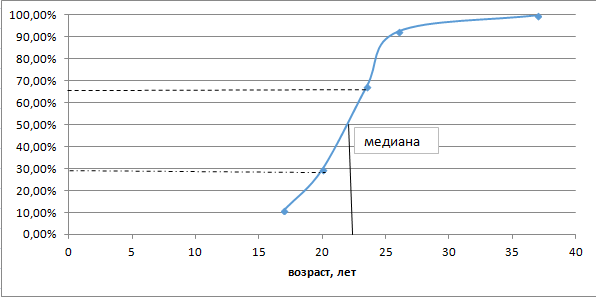
Рисунок 7 – Медиана
Таким образом, в семьях, которые имеют 2-х детей чаще всего возраст родителей при вступлении в барк составляет 34 года.
Задача 3
Рассчитать все виды дисперсий, применить правило сложения дисперсий, объяснить полученные результаты (задание - только для таблицы №7).