Файл: Образовательная программа Компьютерный анализ и интерпретация данных к защите допустить Зав каф. Сиб.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 128
Скачиваний: 2
СОДЕРЖАНИЕ
1.1. Понятие криптографических протоколов передачи данных
1.2. Анализ существующих криптографических протоколов
1.3. Определение требований к протоколу защищенного обмена сообщениями
1.4. Постановка задачи создания защищенного протокола для обмена сообщениями
ГЛАВА 2. КОМПЬЮТЕРНЫЙ АНАЛИЗ ГЕНЕРАТОРОВ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ
2.1. Понятие псевдослучайных чисел и генераторов псевдослучайных чисел
2.1. Линейно конгруэнтный метод
2.2. Регистр сдвига с линейной обратной связью
2.3. Алгоритм «Вихрь Мерсенна»
2.4. Построение и тестирование генераторов псевдослучайных чисел
2.5. Сравнительная характеристика генераторов
ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ РАЗРАБОТАННОГО АЛГОРИТМА
3.1. Аутентификация пользователей
3.2. Получение сеансового ключа
3.3. Генератор псевдослучайных чисел
3.7. Алгоритм целостности данных
ГЛАВА 4. ВЫБОР ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ АЛГОРИТМА
4.1. Ограничения времени сеанса
4.2. Ограничения объема передаваемой информации
4.3. Выбор параметров для алгоритма Диффи-Хеллмана
2.4. Построение и тестирование генераторов псевдослучайных чисел
Для моделирования работы вышеописанных генераторов были использованы среда разработки VS Code, язык программирования JavaScript и программная платформа Node.js, превращающая JavaScript из узкоспециализированного языка в язык общего назначения [21, 22].
Для каждого генератора был описан его подробный алгоритм и создана функция для генерации двоичной последовательности с пользовательскими параметрами (такие, как длина последовательности, число элементов в ней, а также начальное значение при необходимости).
Код функций для каждого метода приведен на рисунке 2.3, а также в таблице 2.4 и таблице 2.5.

Рис. 2.3. Функция для Линейно Конгруэнтного метода
Таблица 2.5
Функция для РСЛОС
 |  |
 | |
Таблица 2.6
Функция для Вихря Мерсенна
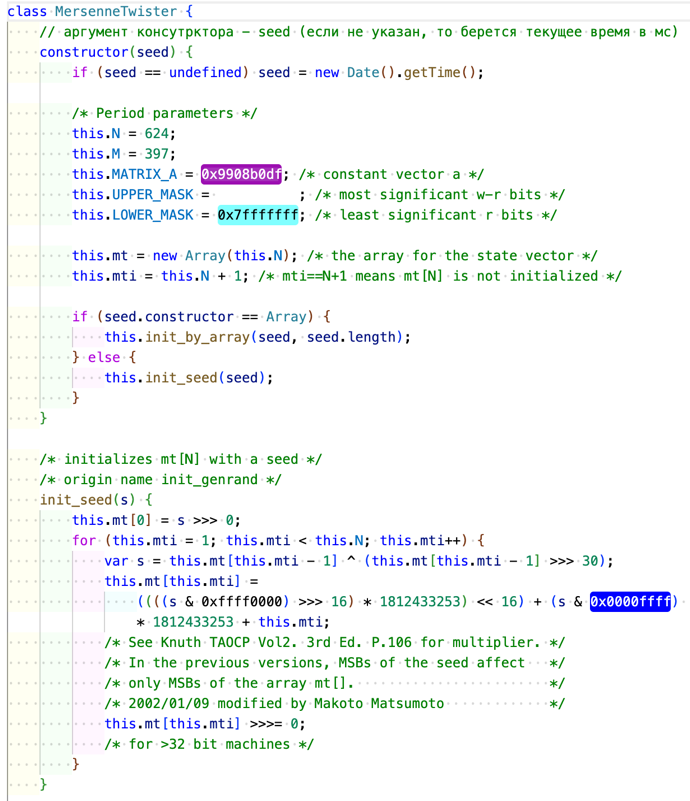 | 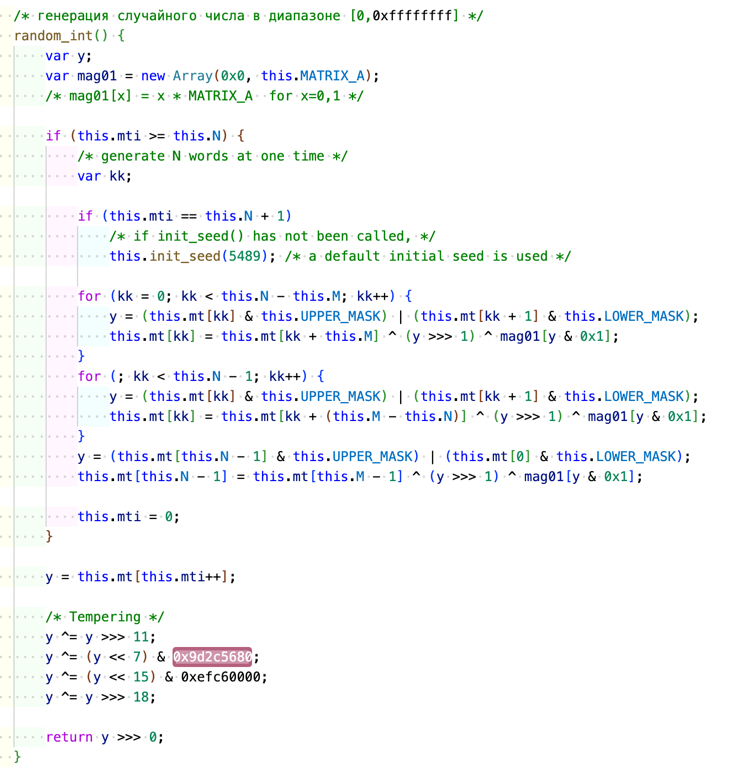 |
 | |
После моделирования каждый из алгоритмов был использован для получения двоичной последовательности, которая состоит из сотни 32-разрядных значений. Выходные последовательности для каждого метода приведены в таблице 2.7.
Таблица 2.7
Выходные последовательности генераторов
| Метод | Последовательность |
| Линейно конгруэнтный метод |  |
| РСЛОС |  |
| Вихрь Мерсенна |  |
Из данной таблицы очевидно, что последовательность, полученная линейно-конгруэнтным методом, имеет определенный паттерн, откуда следует, что качество такой случайной последовательности уже является сомнительным.
Качество работы генераторов можно также оценить с помощью статистических тестов. Тесты позволяют определить качество выдаваемой генератором последовательности чисел, а также то, насколько они безопасны для использования в криптографических системах.
Сущестуют готовые решения для тестирования ГПСЧ. Одним из таких решений является набор статистических тестов NIST (от англ. National Institute of Standards and Technology) [23]. Данный набор содержит множество различных способов для проверки генераторов, таких как частотные тесты бит и блоков, тесты максимальных последовательностей в блоке, тесты матриц и другие.
В данной работе для проверки эффективности алгоритмов были использованы следующие тесты:
1) Частотный побитовый тест. Данный тест определяет соотношение между нулями и единицами в полученной генератором двоичной последовательности. Целью теста является выяснение, является ли соотношение числа единиц и нулей в последователности приблизительно равным, как это было бы в случае генерации истинно случайной бинарной последовательности, где вероятность получения нуля и единицы равная [24]. Неравномерность распределения битов может означать недостаточную случайность последовательности;
2) Тест на последовательность одинаковых битов. Данный тест проверяет, насколько часто в двоичной последовательности встречаются длинные серии (то есть непрерывные подпоследовательности) одинаковых битов. Слишком большое (или, наоборот, слишком малое) наличие таких серий будет означать недостаточную случайность;
3) Тест рангов бинарных матриц. Тест производит расчёт рангов непересекающихся подматриц, построенных из исходной двоичной последовательности. Исходная последовательность разбивается на блоки. Далее эти блоки представляются в виде бинарных матриц, для каждой из которых вычисляется ранг
, т.е. количество линейно независимых строк или столбцов. Целью теста является проверка на линейную зависимость подстрок фиксированной длины, составляющих первоначальную последовательность. Несоответствие рангов матриц ожидаемым значениям может свидетельствовать о недостаточной случайности;
4) Тест на совпадение неперекрывающихся шаблонов. Этот тест проверяет, насколько часто в последовательности встречаются заданные шаблоны фиксированной длины. Для этого исходная последовательность разбивается на блоки, и для каждого блока проверяется, есть ли в нем один из заданных шаблонов. Если количество совпадений сильно отличается от ожидаемого, это может свидетельствовать о недостаточной случайности.
Результаты прохождения тестов отображен в таблице 2.8.
Таблица 2.8
Результаты прохождения тестов NIST
| Генератор | Частотный побитовый тест | Тест на последовательность одинаковых битов | Тест рангов бинарных матриц | Тест на совпадение неперекрывающихся шаблонов |
| Линейно конгруэнтный метод | - | - | - | + |
| РСЛОС | + | + | - | + |
| Вихрь Мерсенна | + | + | + | + |
2.5. Сравнительная характеристика генераторов
Для проведения сравнительного анализа генераторов ПСЧ были использованы следующие критерии: период, равномерность распределения, криптографическая стойкость и скорость генерации ПСЧ. Результаты сравнения показаны в таблице 2.9.
Таблица 2.9
Сравнительный анализ ГПСЧ
| Генератор | ЛКМ | РСЛОС | Вихрь Мерсенна |
| Период | ограниченный (не более m), зависит от выбранных параметров | ограниченный, может быть увеличен путем добавления большего числа регистров | очень большой период, который составляет 219937-1 |
| Скорость | один из самых быстрых ГПСЧ, но его производительность сильно зависит от выбора параметров | высокая скорость работы, может быть медленнее ЛКМ при большом количестве регистров. | обычно имеет достаточно высокую скорость работы, может быть медленнее в сравнении с другими ГПСЧ на некоторых платформах |
| Равномерность распределения | ограниченная равномерность распределения | высокая равномерность распределения | высокая равномерность распределения |
| Криптостойкость | низкий уровень криптографической стойкости | ограниченная криптостойкость, но лучше, чем у ЛКМ | относительно хорошая криптостойкость |
2.6. Выводы
Проведенный анализ алгоритмов генерации ПСЧ продемонстрировал основные преимущества и недостатки каждого метода. Выбирая подходящий ГПСЧ, следует уделить особое внимание не столько самому генератору и его сильным и слабым сторонам, сколько конкретной выполняемой задаче
, в которой требуется применить генератор.
В контексте задачи шифрования сообщений, криптографическая стойкость является одним из наиболее значимых критериев выбора ГПСЧ. Исходя из этого, алгоритм «Вихрь Мерсенна» является наиболее предпочтительным алгоритмом благодаря его большому периоду, высокому уровню криптостойкости и хорошей равномерности распределения. В разработке протокола защищенного обмена сообщениями рекомендуется использовать данный алгоритм.
К похожему выводу также приходят многие исследователи ГПСЧ, например, канадские ученые из Монреальского университета Пьер Л`Экуйе и Ричард Симард [25].
Стоит также отметить, что в задачах, не требующих высокого уровня криптостойкости и большого периода, генераторы типа ЛКМ и РСЛОС также могут быть использованы.
ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ РАЗРАБОТАННОГО АЛГОРИТМА
В данной главе разрабатывается математическое обеспечение для реализации алгоритма шифрования сообщения. Для выполнения данной задачи предлагается использоваться ряд уже существующих криптографических решений: протокол CHAP (Challenge-Handshake Authentication Protocol) для аутентификации пользователей, протокол Диффи-Хеллмана для выработки общего сеансового ключа, генератор псевдослучайных чисел (ГПСЧ) Вихрь Мерсенна. Также непосредственно для шифрования строится таблица замен символов, которая для каждого набранного пользователем символа определяет уникальный двоичный код.
3.1. Аутентификация пользователей
Зачастую, объясняя принципы работы криптографических протоколов, в качестве обозначения общающихся сторон используют имена Алиса и Боб. Далее эти имена будут использоваться в качестве обозначения пользователей.
Перед началом сеанса общения необходимо произвести аутентификацию пользователей для подтверждения их личностей друг перед другом.
Для данной задачи можно использовать различные существующие протоколы, например, PAP, EAP, CHAP или его модификации MS-CHAP.
CHAP (от англ. Challenge-Handshake Authentication Protocol) или Протокол проверки подлинности с вызовом по рукопожатию является наиболее предпочтительным вариантом благодаря его простоте, и в то же время надежности и эффективности способа защиты сетевых подключений [26].
При первом контакте пользователям необходимо обменяться паролями в открытом виде (на доверии). Однако передавать и хранить пароли в исходном виде является плохой практикой, поэтому передаются хеш-суммы от этих паролей.