Файл: Образовательная программа Компьютерный анализ и интерпретация данных к защите допустить Зав каф. Сиб.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 126
Скачиваний: 2
СОДЕРЖАНИЕ
1.1. Понятие криптографических протоколов передачи данных
1.2. Анализ существующих криптографических протоколов
1.3. Определение требований к протоколу защищенного обмена сообщениями
1.4. Постановка задачи создания защищенного протокола для обмена сообщениями
ГЛАВА 2. КОМПЬЮТЕРНЫЙ АНАЛИЗ ГЕНЕРАТОРОВ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ
2.1. Понятие псевдослучайных чисел и генераторов псевдослучайных чисел
2.1. Линейно конгруэнтный метод
2.2. Регистр сдвига с линейной обратной связью
2.3. Алгоритм «Вихрь Мерсенна»
2.4. Построение и тестирование генераторов псевдослучайных чисел
2.5. Сравнительная характеристика генераторов
ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ РАЗРАБОТАННОГО АЛГОРИТМА
3.1. Аутентификация пользователей
3.2. Получение сеансового ключа
3.3. Генератор псевдослучайных чисел
3.7. Алгоритм целостности данных
ГЛАВА 4. ВЫБОР ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ АЛГОРИТМА
4.1. Ограничения времени сеанса
4.2. Ограничения объема передаваемой информации
4.3. Выбор параметров для алгоритма Диффи-Хеллмана
Проверка подлинности пользователей при всех последующих контактах будет происходить по следующему алгоритму:
1) Для запроса на начало сеанса общения Алиса отправляет Бобу свой идентификатор;
2) Боб проверяет, был ли ранее контакт с данным пользоватлеем. Если контакта не было, то Боб сообщает об этом Алисе, и они совершают обмен хеш-суммами паролей.
3) Иначе Боб генерирует случайное открытое число C (challenge) и отправляет его Алисе;
4) Алиса суммирует C с хешем своего пароля, от результата сложения вновь вычисляет хэш-сумму, и это значение отправляет Бобу;
5) Боб, в свою очередь, также суммирует значение C со значением хеш-суммы пароля Алисы, которое было получено и сохранено им при первом контакте, и вычисляет хеш от результата сложения;
6) После этого Боб сравнивает вычисленный результат со значением, полученным от Алисы.
Аутентификация считается успешной, если значения совпадают.
Работа протокола авторизации продемонстрирована на рисунке 3.1.
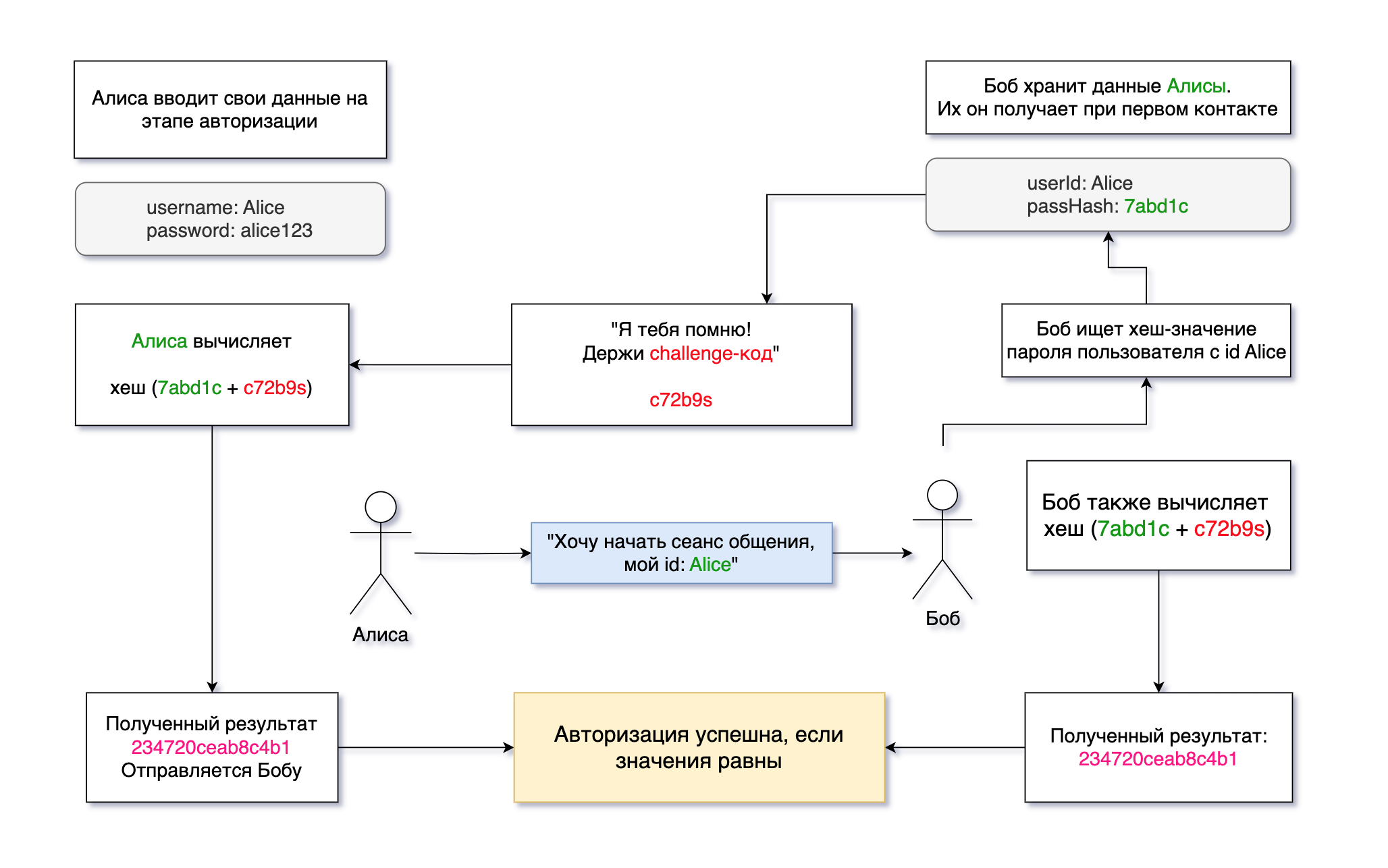
Рис. 3.1. Работа протокола CHAP
Также, для дополнительной защиты вместе с хеш-суммами паролей пользователи могут отправить друг другу MAC-адреса своих устройств. Тогда на 5 и 6 шагах алгоритма Алиса и Боб могут добавить это значение в операцию получения хеша суммы. Таким образом, пользователи смогут общаться друг с другом только при условии правильно введенных паролей и только на тех устройствах, на которых они обменялись своими секретными данными на доверии при первом контакте.
Проверка также может быть двухсторонней, когда оба участника по очереди проверяют подлинность друг друга.
3.2. Получение сеансового ключа
После успешной аутентификации пользователям необходимо установить начальное состояние ГПСЧ. Для этого необходимо сначала произвести выработку общего секретного сеансового ключа. Для этой задачи отлично подходит алгоритм Диффи-Хеллмана, предложенный криптографами Диффи и Хеллманом в работе 1976 года «Новые направления в криптографии» [27].
Данный алгоритм является золотым стандартом в задаче генерации сеансового ключа, используя открытый канал связи. Свое применение алгоритм нашел во множестве криптографических протоколов, таких как TLS/SSL [28].
Криптостойкость алгоритма Диффи-Хеллмана основана на сложности вычисления дискретного логарифма. Существуют математические функции, которые довольно легко вычислить в одну сторону, но в обратную – уже очень сложно. К примеру, если для опреации сложения обратной операцией является вычитание, а для операции умножения – операция деления. Но в то же время существует, к примеру, такая операция как остаток от деления, и обратной операции для нее не существует. Именно данная операция используется в алгоритме Диффи-Хеллмана.
Для описания последовательности действий алгоритма вводятся обозначения, представленные в таблице 3.1.
Таблица 3.1
Обозначения параметров алгоритма Диффи-Хеллмана
| Параметр | Полная запись | Пояснение |
| p | Prime / modulo | |
| g | Generator / base | |
| a | Alice | Секретное число Алисы |
| b | Bob | Секретное число Боба |
Сам алгоритм (рис. 3.2) обмена состоит из следующих действий:
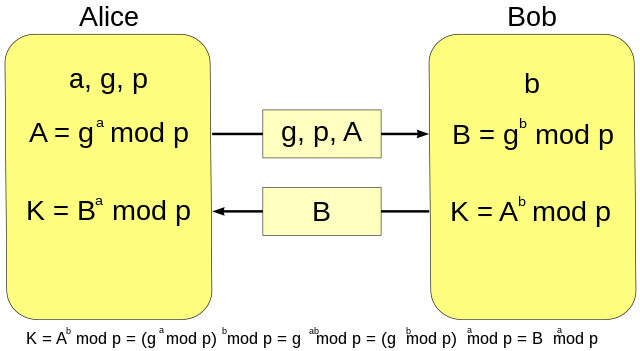
Рис. 3.2. Работа алгоритма Диффи-Хеллмана
1) Алиса выбирает случайные числа p и g (???? – случайное большое простое число, ???? – также простое число, являющееся первообразным корнем по модулю p; для повышения безопасности результат (p-1)/2 также должен быть случайным простым числом), а также число a, удовлетворяющее следующему условию:
| | 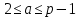 | (3.1) |
Число a является секретным и известно только Алисе;
2) Алиса вычисляет свой открытый ключ
| | 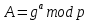 | (3.2) |
и отправляет его Бобу вместе с числами p и g
| | 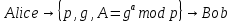 | (3.3) |
3) Боб выбирает случайное число b, также удовлетворяющее условию
| | 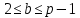 | (3.4) |
Число b является секретным и известно только Бобу;
4) Боб вычисляет общий секретный ключ, используя полученные значения (параметр p и открытый ключ Алисы A):
| | 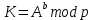 | (3.5) |
Алисе он отправляет свой открытый ключB
| | 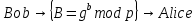 | (3.6) |
5) С помощью этого значения Алиса также вычисляет общий секретный ключ:
| | 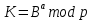 | (3.7) |
Несмотря на разные формулы для вычисления, результат секретных ключей обоих сторон одинаковый:
| | 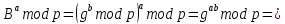 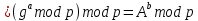 | (3.8) |
Результат данного этапа – общий секретный ключ, полученный пользователями.
3.3. Генератор псевдослучайных чисел
Следующий этап алгоритма – получение двоичной последовательности из ГПСЧ. В качестве генератора можно использовать Алгоритм Фон-Неймана, Линейно-Конгруэнтный метод, Регистр Сдвига с Линейной обратной связью или Вихрь Мерсенна. При проведении сравнительного анализа, описанного в предыдущей главе, был выбран последний вариант.
В качестве начального значения для генератора используется общий сеансовый ключ, полученный на предыдущем шаге алгоритма. Вихрь Мерсенна, как и любой другой ГПСЧ, выдает не истинно случайные числа, а результаты вычислений определенного алгоритма, поэтому оба участника общения гарантированно будут иметь одинаковый результат работы при равных параметрах генератора, в том числе начального состояния.
3.4. Таблица замен символов
Последовательность, полученная из ГПСЧ, используется для шифрования сообщения, но перед шифрованием необходимо сначала привести исходное сообщение из буквенного вида в числовой, а именно – в последовательность двоичных чисел.
Сперва необходимо определить общее число символов, которые будут использоваться для составления сообщений. Минимумом является следующий набор:
1) 66 букв для кириллицы в двух регистрах;
2) 52 буквы для латиницы в двух регистрах;
3) 10 цифр;
Также, помимо букв и цифр потребуется как минимум 8 специальных символов, а именно:
1) пробел;
2) символ переноса строки;
3) точка;
4) запятая;
5) восклицательный знак;
6) вопросительный знак;
7) двоеточие;
8) косая черта «/».
Последние три символа являются составляющими ссылок, которые также могут присутствовать в пересылаемом сообщении.
Итого получается 136 символов. Далее необходимо построить таблицу замен, в которой каждому символу будет присвоено уникальное двоичное значение. При шифровании каждый символ сообщения будет переведен по этой таблице, в результате чего получится бинарная последовательность.
Для однозначной интерпретации символов в последовательности, длина каждого двоичного числа должна быть одинаковой.