Файл: Образовательная программа Компьютерный анализ и интерпретация данных к защите допустить Зав каф. Сиб.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 120
Скачиваний: 2
СОДЕРЖАНИЕ
1.1. Понятие криптографических протоколов передачи данных
1.2. Анализ существующих криптографических протоколов
1.3. Определение требований к протоколу защищенного обмена сообщениями
1.4. Постановка задачи создания защищенного протокола для обмена сообщениями
ГЛАВА 2. КОМПЬЮТЕРНЫЙ АНАЛИЗ ГЕНЕРАТОРОВ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ
2.1. Понятие псевдослучайных чисел и генераторов псевдослучайных чисел
2.1. Линейно конгруэнтный метод
2.2. Регистр сдвига с линейной обратной связью
2.3. Алгоритм «Вихрь Мерсенна»
2.4. Построение и тестирование генераторов псевдослучайных чисел
2.5. Сравнительная характеристика генераторов
ГЛАВА 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ РАЗРАБОТАННОГО АЛГОРИТМА
3.1. Аутентификация пользователей
3.2. Получение сеансового ключа
3.3. Генератор псевдослучайных чисел
3.7. Алгоритм целостности данных
ГЛАВА 4. ВЫБОР ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ АЛГОРИТМА
4.1. Ограничения времени сеанса
4.2. Ограничения объема передаваемой информации
4.3. Выбор параметров для алгоритма Диффи-Хеллмана
Далее, после ряда преобразований, уже измененная бинарная последовательность будет переведена обратно в символы.
На данном этапе может возникнуть ситуация, когда для перевода двоичного числа в таблице замен не будет соответствующего ему символа, поэтому таблицу нужно изменить так, чтобы она содержала все возможные комбинации чисел для заданной длины. Достигнуть этого можно при общем числе символов, равному степени двойки, то есть 2n. Ближайшая для 136 степень двойки – это 128.
Для того, чтобы убрать из таблицы 8 лишних значений, и при этом не ограничить пользователя в символах, можно задать 4 буквам из кириллического алфавита («а», «с», «е» и «о») значения схожих по написанию латинских букв.
При переводе по таблице двоичных чисел в один из этих четырех символов будет использоваться буква латинского алфавита, так как в ссылках требуется английская раскладка, тогда как в обычном тексте раскладка не имеет большого значения.
Таким образом, общее число символов в таблице замен – 128 (или 27), а диапазон значений в двоичном представлении – от 0000000 до 1111111, то есть для любого 7-битного двоичного значения в таблице гарантировано будет соответствующий символ.
Для улучшения криптостойкости можно производить сдвиг таблицы на M позиций, где M – это число в диапазоне от 0 до 127 (или от 0000000 до 1111111) включительно. 0 означает отсутствие сдвига таблицы, 0000001 – сдвиг на 1 позицию, 1111111 – сдвиг на 127 позиций и т.д.
В качестве значения M могут использоваться первые 7 символов из двоичной последовательности, которая получается из ГПСЧ. Эта последовательность будет обозначаться как shiftPartGen.
Оставшиеся символы последовательности leftPartGen будут использованы для шифрования.
Пример нескольких записей в таблице замен при сдвиге на 2 символа приведен на рисунке 3.3.

Рис. 3.3. Пример записей в таблице замен символов
Также можно задавать значения кодов для символов в произвольном, неалфавитном порядке. Например, если 0000000 соответсвтует цифра 1, то для 0000001 назначить не следующую за единицей цифру 2, а какой-нибудь специальный символ или букву.
На практике для создания таблицы замен символов можно использовать тип данных, реализующий хранение пар вида «(ключ, значение)». Этот тип данных также носит название «ассоциативный массив». В качестве примера могут выступать такие структуры данных, как деревья поиска или хеш-таблицы.
Главным достоинством ассоциативных массивов является то, что операция поиска у них имеет логарифмическую сложность (3.9).
| | 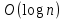 | (3.9) |
, где n – текущее количество хранимых пар.
Данный показатель является одним из лучших среди временных сложностей алгоритмов, а высокая скорость – одно из ключевых требваний разрабатываемого алгоритма.
3.5. Шифрование сообщения
Полученная таблица замен символов используется для шифрования отправляемого сообщения.
На первом этапе шифрования исходное сообщение разбивается на символы, находятся все вхождения букв «а», «с», «е» и «о» кириллического алфавита, производится их замена на схожие по написанию буквы латинского алфавита.
Далее каждый символ преобразуется по таблице замен в соответствующее семизначное двоичное число.
В случае, если некоторые символы не будут распознаны (то есть если в таблице не будет соответствующих им значений), то в качестве двоичного значения для таких символов можно указать значение какого-либо определенного символа, например, символа «?».
Полученный набор чисел объединяется в одну общую последовательность encrText длины N(рис. 3.4).

Рис. 3.4. Первичное преобразования исходного сообщения
Далее из начала последовательности leftPartGen вырезается часть символов такой же длины. Эта часть обозначается как nPartGen. Оставшаяся часть leftPartGen будет использоваться при шифровании следующих сообщений. На рисунке 3.5 показан пример получения обозначенных значений из псевдослучайной последовательности.

Рис. 3.5. Получение значений из последовательности ГПСЧ
Следующим шагом производится операция сложения по модулю 2 (также называемая XOR или «исключающее ИЛИ») двоичных чисел encrText и nPartGen (рис. 3.6).

Рис. 3.6. Вычисление суммы по модулю два
Битовые операции, такие как исключающее ИЛИ, как правило требуют наименьших ресурсов, чем операции с целочисленными значениями, так как они работают с битами напрямую, а на простых процессарах зачастую еще и имеют большую скорость работы. Это является большим достоинством для разрабатываего протокола, так как скорость обработки информации является одним из ключевых требований при разработке.
Однако, стоит отметить, что на практике скорость выполнения операций зависит от конкретной реализации и аппаратной платформы.
Полученная после операции сложения по модулю два последовательность разбивается на 7-битовые двоичные числа, и далее каждое из них преобразуется по таблице замен в символьный вид, в результате чего получается нечитаемый набор букв (рис. 3.7).

Рис. 3.7. Результат шифрования
Помимо текста в качестве исходного сообщения может быть отправлена ссылка, для которой в таблице замен символов имеются все необходимые обозначения. Благодаря поддержке отправки ссылок пользователи также могут делиться друг с другом медифайлами, такими как изображения, видео или аудио. Для этого им требуется предварительно загрузить необходимый файл в какое-либо облачное хранилище, получить ссылка на загруженный ресурс и зашифровать ее.
3.6. Расшифровка сообщения
Для расшифрования полученного сообщения его необходимо разбить на символы, после чего каждый символ переводится по таблице замен в двоичное число (рис. 3.8).
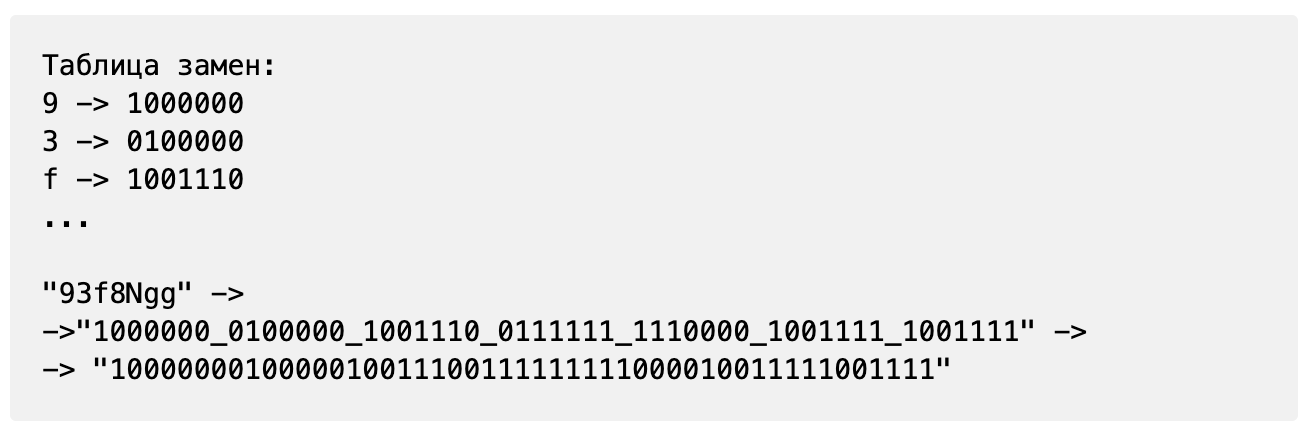
Рис. 3.8. Первичное преобразования зашифрованного сообщения
Далее все двоичные числа объединяются в одно число. Полученная двоичная последовательность decrText длины N складывается по модулю два с числом nPartGen, полученному принимающей стороной из генератора.
Благодаря одинаковому начальному состоянию ГПСЧ на обеих сторонах значение nPartGen также будет одинаковым.
В силу того, что операция сложения по модулю два является обратимой, имея результат операции (decrText) и один из операндов (общее значение nPartGen) получается второй операнд – encrText (рис. 3.9).

Рис. 3.9. Вычисление encrText
Полученное значение encrText разбивается на двоичные числа по 7 бит, и каждое из них переводится в символ по таблице замен. Полученные значения объединяются.
На выходе будет исходное сообщение, отправленное первым пользователем (рис. 3.10).

Рис. 3.10. Результат расшифровки