ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 131
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.2 Решение системы дифференциальных уравнений
4. РАЗРАБОТКА СИСТЕМЫ ДЛЯ ПИТАНИЯ ВЕНТИЛЬНЫХ ДВИГАТЕЛЕЙ
4.1 Обоснование, выбор и описание функциональной схемы электропривода
4.2 Описание и построение структурной схемы электропривода
4.3 Разработка и описание принципиальной электросхемы датчика контроля состояния вентилей
4.4 Разработка и описание принципиальной электросхемы системы импульсно-фазового управления
4.5 Расчет и выбор элементов датчика контроля состояния вентилей
4.6 Расчет и выбор элементов системы импульсно-фазового управления
2.2 Решение системы дифференциальных уравнений
В качестве объекта моделирования выступает вентильно-индукторный двигатель (ВИД), который включает машину, аналогичную полюсному индуктору, с рядом переключателей возбуждения и инверторов, ключ которых управляется сигналами датчика ротора и, в целом, других датчиков, например датчик тока. Вариант схемы участка питания вентильно-индукторного двигателя показан на рисунке 2.1.
Учитывая полноту магнитной цепи и отсутствие синусоидального переменного тока, метод мгновенных значений, в котором магнитная цепь, токи и напряжения рассчитываются путем повторения электромагнитного процесса с небольшими шагами, подходит для численного представления электромагнитной активности, происходящей в вентильно-индукторных двигателях. С помощью этого метода можно точно моделировать не только процессы, происходящие в электричестве, но и учитывать при моделировании коммутационных машин факторы, вносимые переключающимися клапанами [7].
Математическая модель электромеханической системы представляет собой систему уравнений, которая объединяет и описывает исследуемый процесс. С практической точки зрения интересна не сама математика, а реализация программ на сложных языках программирования, которые могут рассчитывать и анализировать параметры электрических машин.
Основной информацией электротехники являются численные, геометрические и схемотехнические свойства электрических машин, полупроводников, коммутационных устройств, элементов схем, а также параметры методологии исследования. Вращение ротора пропорционально изменению электрического угла , характеризующее положение ротора относительно статора, и шаг.
Основной составляющей уравнения является система уравнений, описывающих согласно закону Кирхгофа характер токов, протекающих в цепи. Это уравнение основано на выражении напряжения, записанном для каждой переменной: m фазы обмотки якоря (AW) и s возбуждения (EF). Для i-й переменной уравнение выглядит так:
| ui=ii·Ri+di/dt , | (2.1 |
где ui; ii
; Ri; i – напряжение, ток, сопротивление и потокосцепление i-той обмотки соответственно;
di/dt – ЭДС, наведенная в i-ой обмотке в рассматриваемый момент времени.
При расчете сопротивления фазы учитывается рабочая температура двигателя tr:
| R=R20·(1+kTR·(tр-20)), | (2.2 |
| | |
где R20– сопротивление фазной обмотки якоря, соответствующее температуре 20oС; kTR– температурный коэффициент сопротивления (для меди kTR=0,004 oС-1).
Учитывая, что изменение потокосцепления может быть вызвано изменением положения ротора и ветра при преобразовании электрической машины уравнение (2.1) в развернутом виде имеет вид:
| ui =iiRi+iddt+ 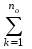 iikdik/dt , iikdik/dt , | (2.3 |
где i - коэффициент ЭДС вращения eврi;
ddt= - электрическая угловая скорость вращения (
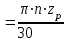 );
);n – частота вращения ротора об/мин;
zр – число зубцов ротора;
iik – дифференциальная индуктивность Lik.
Полная эквивалентная схема схемы, соответствующая режиму ВИД и включающая эквивалентную схему обмоток, инвертор, источник питания и выпрямитель, показана на рисунке 2.1. Полупроводниковые элементы (диоды и транзисторы) в схеме представляются как нелинейные элементы, их характеристиками являются вольт-амперные характеристики.
Кривые, определяемые системой дифференциальных уравнений, определяются с учетом полупроводниковых свойств элементов переключающего вентиля (инвертора и выпрямителя). Ниже приведен пример записи уравнения для одной из цепей (на рис. 2.1 цепь показана штриховой линией) при протекании тока в частях А и В (ic = 0) электродвигателя.
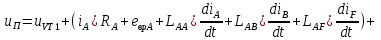 | (2.4 |
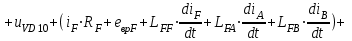 | |
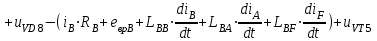 , , |
Где
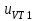 ,
,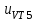 - падение напряжения на транзисторах VT1 и VT5;
- падение напряжения на транзисторах VT1 и VT5;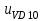 ,
,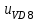 - падение напряжения на диодах VT10 и VT8.
- падение напряжения на диодах VT10 и VT8.Алгоритм переключения транзисторов задается системой управления по сигналу датчика ротора и другим требованиям. Соотношение между временем включения фазы и мощностью источника питания и ротора определяет фазовый угол. Помним, что фазовый угол определяется как электрический угол между пересечением нуля положительной частью круговой ЭДС фазы и временем, когда фаза подключена к мощности от источника положительного потока.
Процесс выступает в качестве неизвестного в полученной системе дифференциальных уравнений. Производные рассчитываются методами исключения Гаусса, а вот ток (относительно следующего положения ротора) - по формуле Эйлера:
| i(t+t)=i(t)+di/dt·t, | 2.5 |
Где t - интервал времени, соответствующий количеству шагов : т"="/.
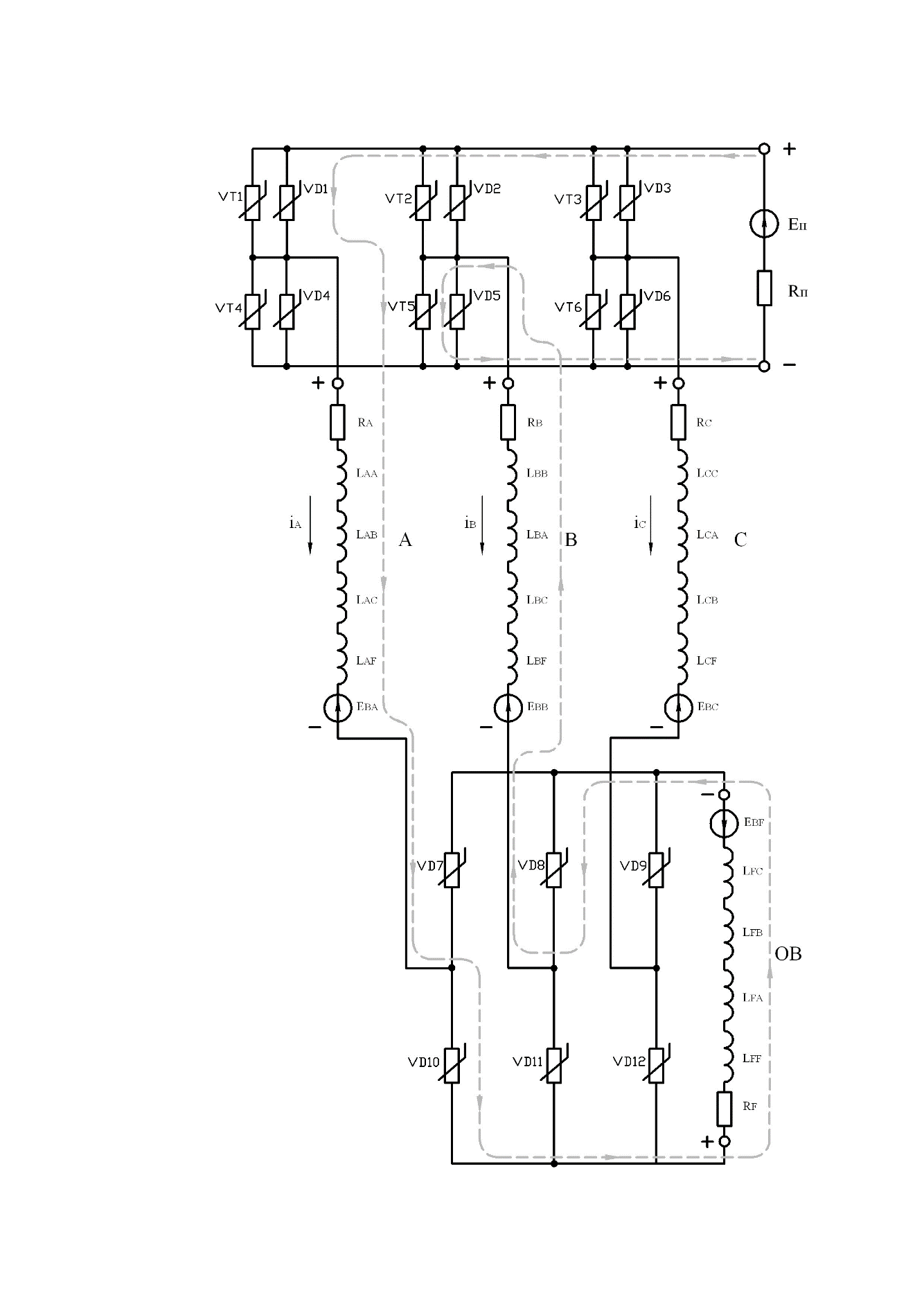
Рисунок 2.1 - Схема вентильно-индукторного двигателя судна
Различные параметры электронного магнитного поля - коэффициент вращающейся ЭДС и различная индукция - определяются после определения магнитных свойств ферромагнитных частей цепи.
Расчет магнитопровода производиться по электрическому току. Для этого разделим магнитопровод электрической машины на несколько частей, каждая из которых имеет простую форму и состоит из материала с магнитной характеристикой В(Н).
В каждой выбранной части магнитной катушки с равным вращением возникает магнитный ток, величина которого зависит от геометрического баланса фаз между магнитной катушкой и магнитным полем, причем для ферромагнитной части линии не зависят от магнитного поля.
В случае вентильно-индукторной машины с вращающимися зубьями якоря и двигателем возбудителя вне ротора, магнитную цепь легко уменьшить с помощью зубьев статора, зубьев ротора, воздушного зазора, втулки, корпуса, вращающегося возбудителя и якоря. В зависимости от решаемой задачи и требований точного расчета, отдельные компоненты могут быть исключены или, наоборот, детализированы. Точность и время, необходимое для расчета механических свойств, зависят от степени детализации схемы.
Стандартные скорости потока ВИД с различными уровнями детализации показаны на рисунке 2.2.-2.3. Следующие имена были введены в эквивалентный список:
| G | - | Сs − суммарная магнитная сила внутреннего и продольного распределения якоря переменная; | |
| G | - | C -плотность магнитного потока j-го зубца статора; | |
| G | - | ps − дисперсия магнитного поля; | |
| G | - | ri −магнитное поле i-го зубца ротора; | |
| G | - | Fs − магнитная проводимость рассеяния обмотки возбуждения; | |
| G | - | δji магнитное поле воздушного пространства между j-м зубцом и i-м зубцом ротора. | |
| В схеме, аналогичной рисунку 2.2 | |||
| | - | k полная магнитная проводимость корпуса; | |
| | | вт полные цепи магнитного поля. | |

Рисунок 2.2 - Эквивалентная схема магнитопровода ВИД
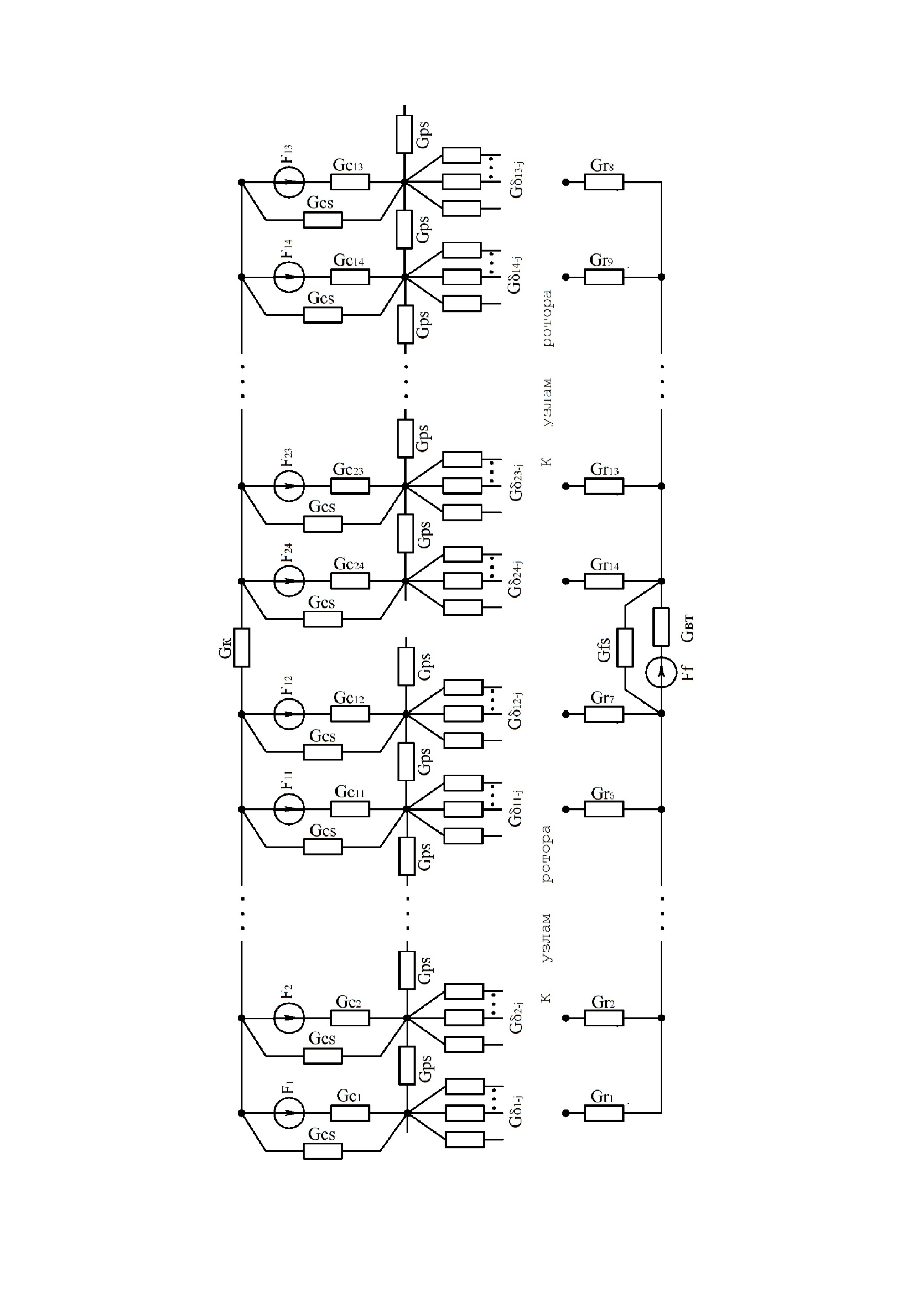
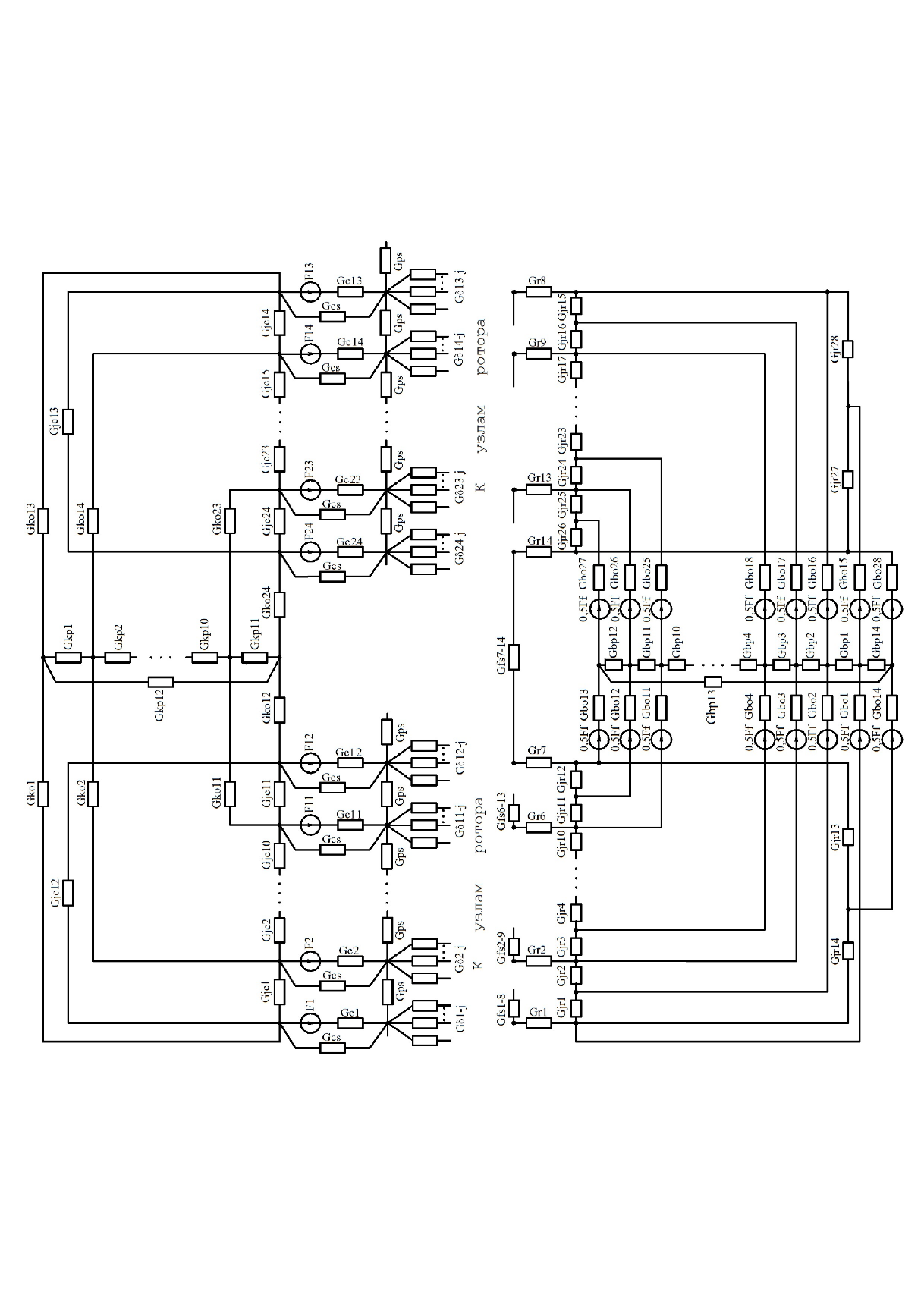

Рисунок 2.3 -Полный ВИД эквивалент магнитного поля
| В схеме, аналогичной рисунку 2.3 | ||
| Gjc | - | магнитное поле j-го сечения спинки статора; |
| Gjr | - | магнитное поле i-й секции ярма ротора; |
| Gko | - | магнитная проводимость продольного участка корпуса; |
| Gkp | - | корпус поперечного сечения магнитного поля; |
| Gbo | - | магнитная проводимость продольного участка втулки; |
| Gbp | - | магнитная проводимость поперечного участка втулки; |
Основными элементами эквивалентной схемы являются:
| Fj | - | j-я обмотка якоря МДС; |
| Ff | - | Суммарная МДС обмотки возбуждения. |
Следует отметить, что эквивалентную схему многопакетной индукторной машины можно привести к эквивалентной схеме двухкорпусной модели, учитывая это изменение при расчете ЭДС и индукции через материал. Кроме того, в том же корпусе возможна простая эквивалентная схема. Если число зубьев статора zс и число зубцов ротора zr имеют общий знаменатель kd, то магнитопровод электродвигателя можно рассматривать как kd интегральную систему, где одна независимая электронная цепь. При этом эквивалентную схему можно создать только в одной области. Остальная часть машины учитывается с помощью коэффициентов kd для проводимости, ЭДС и индуктивности.
-
Моделирование вентильного двигателя
MATLAB − пакет прикладных программ для решения задач технических вычислений и одноимённый язык программирования, используемый в этом пакете. Пакет используют более миллиона инженерных и научных работников, он работает на большинстве современных операционных систем.
Simulink – это графическая среда имитационного моделирования, позволяющая при помощи блок-диаграмм в виде направленных графов, строить динамические модели, включая дискретные, непрерывные и гибридные, нелинейные и разрывные системы. Интерактивная среда Simulink, позволяет использовать уже готовые библиотеки блоков для моделирования электросиловых, механических и гидравлических систем, а также применять развитый модельно-ориентированный подход при разработке систем управления, средств цифровой связи и устройств реального времени.
Дополнительные пакеты расширения Simulink позволяют решать весь спектр задач от разработки концепции модели до тестирования, проверки, генерации кода и аппаратной реализации. Simulink интегрирован в среду MATLAB, что позволят использовать встроенные математические
алгоритмы, мощные средства обработки данных и научную графику.
Построим структурную модель вентильно-индукторного двигателя для исследования нагрузки и частоты вращения (рис. 2.4).
Особенностью этой модели является использование стандартных блоков из библиотеки SimPowerSystem. В блоке Converter моделируется 3-х фазный преобразователь для питания ВИД, состоящий из двух транзисторов, подключающих каждую фазу к источнику питания, блок Switched Reluctance Motor моделирует работу ВИД. В блоке Position_Sensor реализована простейшая стратегия управления двигателем.