Файл: Федеральное агентство по рыболовству Федеральное государственное бюджетное образовательное.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 96
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вычислим среднюю квадратическую погрешность квантования (СКПК).
В процессе квантования образуется специфическая погрешность q,k, называемая шумом квантования. Средняя квадратическая погрешность квантования (мощность шума квантования) рассчитывается по формуле (11):
где Px и Py соответственно мощности (дисперсии) входного и выходного сигналов квантователя; Bxy - коэффициент взаимной корреляции между этими сигналами, который рассчитывается по формуле (12):
WX (x) - ФПВ гауссовской величины X. В результате получаем:
Коэффициент Ky рассчитывается по формуле (13):
где Pn - распределение вероятностей дискретной случайной величины y = x (n).
Pn рассчитывается по формуле (14):
 (14)
(14)где Ф (v) - функция Лапласа.
Отсюда: Ky =1,083.
Итак, средняя квадратическая погрешность квантования:
С помощью таблиц 2 и 3 строим характеристику квантования (рис.8).
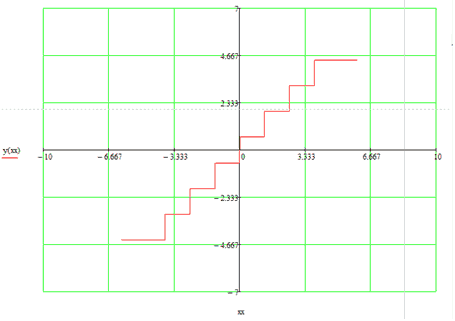
Рисунок 8 - Характеристика квантования
5. Расчет закона и функции распределения вероятностей квантованного сигнала, а также энтропии, производительности и избыточности L - ичного дискретного источника
Квантованная последовательность yk = xk (n) c учетом независимости ее значений определяется одномерным распределением вероятностей по формуле (14).
Таблица 4. Расчет распределения вероятностей дискретной случайной величины
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| | 0.00135 | 0.021 | 0.136 | 0.341 | 0.341 | 0.136 | 0.021 | 0.00135 |
Интегральное распределение вероятностей рассчитывается по формуле (15):
Таблица 5. Расчет распределения вероятностей квантованного сигнала
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Fn | 0.00135 | 0.023 | 0.159 | 0.5 | 0.841 | 0.977 | 0.999 | 1 |
Найдем энтропию L-ичного дискретного источника.
Энтропия - среднее количество информации, содержащейся в одном из символов (букв, цифр) алфавита.
Энтропию находим по формуле (16):
Производительность (скорость ввода информации в ДКС) определяется формулой (17):
Избыточность источника рассчитываем по формуле (18):
Построим в масштабе графики рассчитанных закона и функции распределения вероятностей.
С помощью таблицы 4 строим график закона распределения вероятностей, а согласно таблице 5 покажем функцию распределения вероятностей.
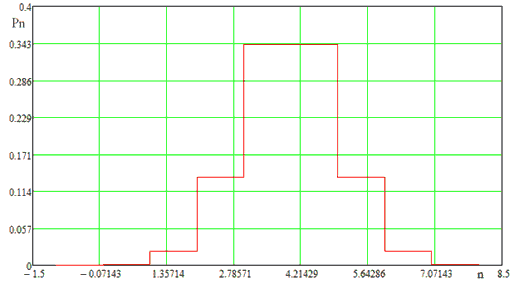
Рисунок 9 - График закона распределения вероятностей
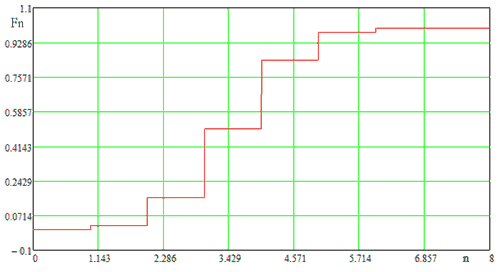
Рисунок 10 - Функция распределения вероятностей
6. Кодирование значения L-ичного дискретного сигнала двоичным блочным примитивным кодом. Построение таблицы кодовых расстояний кода
В кодере АЦП последовательность xk (n) преобразуется в последовательность кодовых символов {bi}. Физические уровни x (n) вначале заменяются их номерами
 (19)
(19)где bn,j - двоичный кодовый символ десятичного числа n, расположенный в j-й позиции кодовой комбинации.
Расстояние Хэмминга - число позиций, в которых соответствующие символы двух слов одинаковой длины различны. Первоначально метрика была сформулирована Ричардом Хэммингом для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга
d (x,y) между двумя двоичными последовательностями (векторами) x и y длины n называется число позиций, в которых они различны.
Кодовое расстояние Хэмминга dmn между двумя двоичными кодовыми комбинациями
 (20)
(20)Все возможные кодовые комбинации: {000, 001, 010, 011, 100, 101, 110, 111}
Таблица 6. Таблица кодовых расстояний
| | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 000 | 0 | 1 | 1 | 2 | 1 | 2 | 2 | 3 |
| 001 | 1 | 0 | 2 | 1 | 2 | 1 | 3 | 2 |
| 010 | 1 | 2 | 0 | 1 | 2 | 3 | 1 | 2 |
| 011 | 2 | 1 | 1 | 0 | 3 | 2 | 2 | 1 |
| 100 | 1 | 2 | 2 | 3 | 0 | 1 | 1 | 2 |
| 101 | 2 | 1 | 3 | 2 | 1 | 0 | 2 | 1 |
| 110 | 2 | 3 | 1 | 2 | 1 | 2 | 0 | 1 |
| 111 | 3 | 2 | 2 | 1 | 2 | 1 | 1 | 0 |
Рассчитываем априорные вероятности передачи по двоичному ДКС (дискретному каналу связи) символов нуля и единицы, начальную ширину спектра сигнала ИКМ (импульсно - кодовой модуляции).
Априорные вероятности передачи символов 1 и 0 определяются из формул (21) и (22):
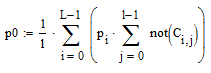 (21);
(21);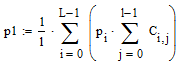 (22)
(22)где Сi,j - элемент матрицы кодовых комбинаций;
оператор not - оператор логического отрицания. Указанные вероятности равны p (1) = p (0) = 0.5.
Ширина спектра сигнала ИКМ вычисляется по формуле (23):
 (23)
(23)где fд - частота дискретизации;
K1=1,667 - постоянная.
Построим графики сигналов в четырех сечениях АЦП (аналого-цифровой преобразователь): вход АЦП, выход дискретизатора, выход квантователя, выход АЦП.
Сигнал на входе АЦП представлен на рисунке 11.
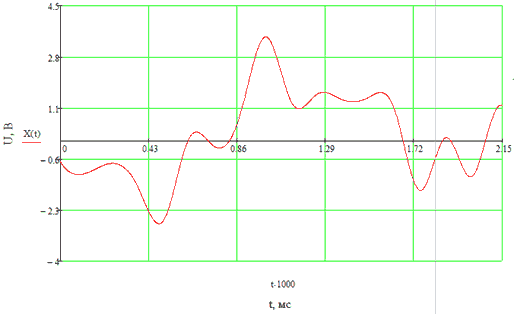
Рисунок 11 - Сигнал на входе АЦП
Сигнал на выходе дискретизатора представлен на рисунке 12.
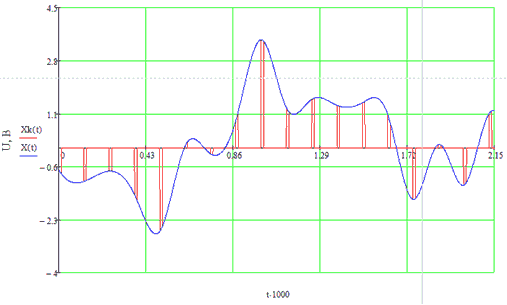
Рисунок 12 - Сигнал на выходе дискретизатора
Сигнал на выходе квантователя представлен на рисунке 13.
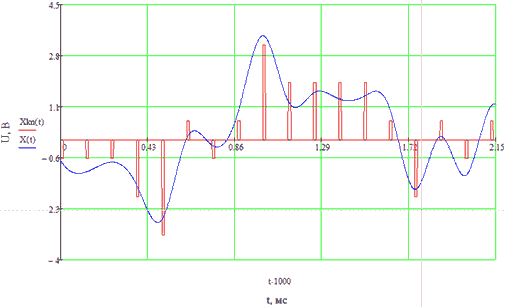
Рисунок 13 - Сигнал на выходе квантователя
Сигнал на выходе АЦП представлен на рисунке 14.
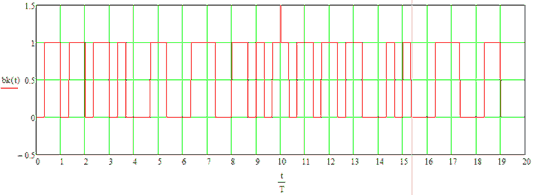
Рисунок 14 - Сигнал на выходе АЦП