Файл: Методы проверки гипотез о положении и рассеивании значений параметров в биометрии.doc
Добавлен: 01.12.2023
Просмотров: 124
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1 Проверка гипотезы о равенстве средних при равных дисперсиях
1.2 Проверка гипотезы о равенстве средних при связанных выборках
2.1 Проверка гипотезы о равенстве средних при равных дисперсиях (на примере двух выборок)
2.2 Проверка гипотезы о равенстве средних при связанных выборках
Содержание
Задание 3
Введение 4
1 Теоретическая часть 6
1.1 Проверка гипотезы о равенстве средних при равных дисперсиях 6
1.2 Проверка гипотезы о равенстве средних при связанных выборках 7
2 Практическая часть 9
2.1 Проверка гипотезы о равенстве средних при равных дисперсиях (на примере двух выборок) 9
2.2 Проверка гипотезы о равенстве средних при связанных выборках 11
2.3 Построение графиков законов распределения 13
Заключение 17
Список использованных источников 18
Задание
Тема:
Методы проверки гипотез о положении и рассеивании значений параметров в биометрии.
1) Общие понятия и определения.
2) Последовательность операций при выборе критерия.
3) Определение класса применяемого критерия (параметрическая или непараметрическая).
4) Требования к выборкам.
5) Примеры и выводы.
Введение
Общая теория и вероятностные методы статистики в медицине включают методологию медико-статистического исследования, т.е. совокупность специфических научных методов и приемов сбора, обработки, анализа и оценки медико-статистической информации. Основными методами статистических исследований являются статистическое наблюдение (включая методы планирования и организации); группировка и сводка материалов наблюдения; методы первичной статистической обработки данных (вычисление производных величин – средних и относительных, критериев их достоверности); метод выборочного медико-статистического исследования, включая оценку репрезентативности (представительности) выборочных данных; методы математико-статистического анализа: статистическая оценка значимости различий сравниваемых показателей, исследование и оценка связей и взаимозависимостей, исследование динамики явлений и процессов, статистическое планирование эксперимента, прогнозирование, многомерный статистический анализ, графический анализ и др.
Медико-статистическое исследование включает пять самостоятельных, но взаимосвязанных этапов: 1) планирование исследования (формулировка цели, разработка задач, программы и плана исследования); 2) статистическое наблюдение (сбор материала для его последующей статистической обработки); 3) статистическая группировка и сводка материалов наблюдения: 4) первичная статистическая обработка данных; 5) научно-статистический анализ, графическое и литературное оформление результатов исследования.
Несмотря на наличие этапов, медико-статистическое исследование представляет собой единое, органически связанное целое, в основе которого лежит целостный, системный подход к изучаемому объекту.
Объектом медико-статистического исследования являются массовые процессы, происходящие среди населения, в сферах оказания медпомощи и проведения санитарно-противоэпидемических мероприятий, анализ которых позволяет вскрыть и охарактеризовать количественно закономерности и особенности здоровья населения в целом и составляющих его групп, развитие и течение болезней среди различных групп населения, деятельность органов и учреждений здравоохранения.
Статистика здоровья населения разрабатывает специфические методы и приемы сбора, обработки, анализа и оценки медико-статистической информации обо всех процессах и явлениях, характеризующих состояние и динамику здоровья населения, его качественно однородных групп в связи с конкретными социальными, экономическими и природными условиями: демографические процессы, физическое развитие, заболеваемость населения, временная нетрудоспособность, инвалидность и др.
Статистика здравоохранения создает специфические методы и приемы сбора, обработки, передачи, хранения, анализа и оценки информации о состоянии и изменениях сети учреждений и органов здравоохранения, их деятельности, кадров здравоохранения, медико-санитарного имущества и др.
Важное место занимают фактические медико-статистические данные, регулярно собираемые, обрабатываемые, анализируемые и используемые в повседневной оперативной работе учреждениями и органами здравоохранения, а также направляемые в строго установленном порядке по подчиненности в виде специальных документов государственной медицинской отчетности. С этой целью в системе здравоохранения создана медико-статистическая служба, низовым звеном которой являются кабинеты медицинского учета и статистики медицинских учреждений. Главной задачей этой службы является обеспечение учреждений и органов здравоохранения достоверной, полной и своевременной информацией.
1 Теоретическая часть
1.1 Проверка гипотезы о равенстве средних при равных дисперсиях
Пусть из каждой из двух нормально распределенных генеральных совокупностей
Случай, когда дисперсии генеральных совокупностей
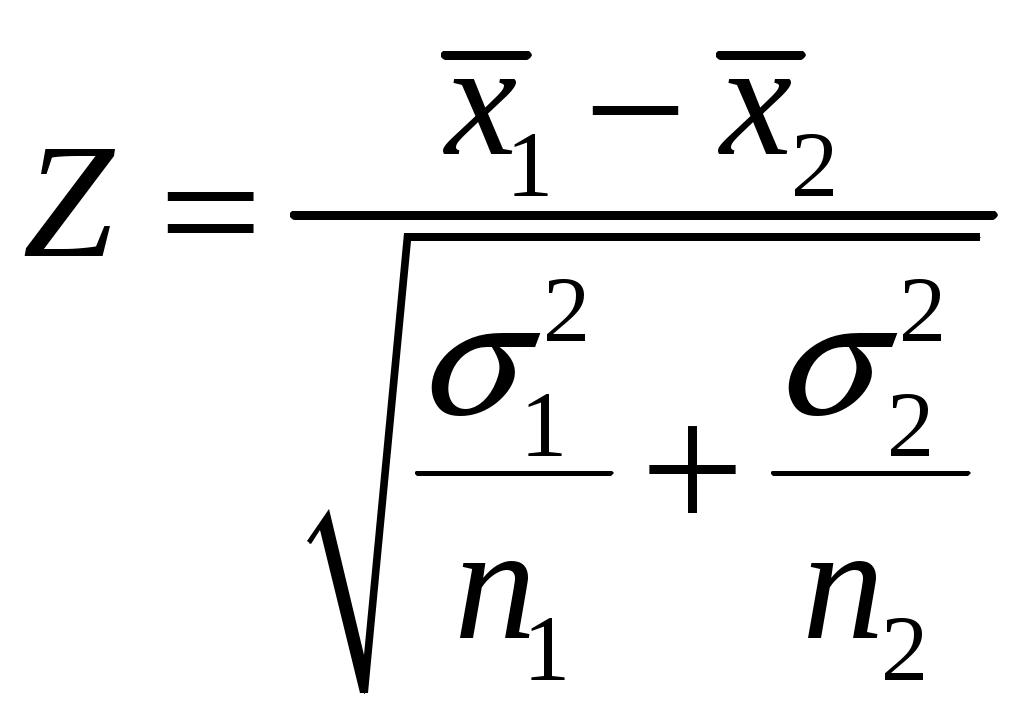 ,
,где
имеет нормальное распределение с математическим ожиданием, равным нулю и дисперсией, равной единице. Критическое значение выбирается в соответствии с задаваемым уровнем значимости по таблице значений функции Лапласа или стандартного нормального распределения.
Если объемы выборок достаточно велики
Эту же статистику используют и при проверке гипотезы о равенстве вероятностей «успеха». Объемы выборок
1.2 Проверка гипотезы о равенстве средних при связанных выборках
Критерий Стьюдента (t-критерий) позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности».
При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно.
Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми