Файл: Методы проверки гипотез о положении и рассеивании значений параметров в биометрии.doc
Добавлен: 01.12.2023
Просмотров: 120
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1 Проверка гипотезы о равенстве средних при равных дисперсиях
1.2 Проверка гипотезы о равенстве средних при связанных выборках
2.1 Проверка гипотезы о равенстве средних при равных дисперсиях (на примере двух выборок)
2.2 Проверка гипотезы о равенстве средних при связанных выборках
, связанными.
В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.
Вычисление значения t осуществляется по формуле:
,
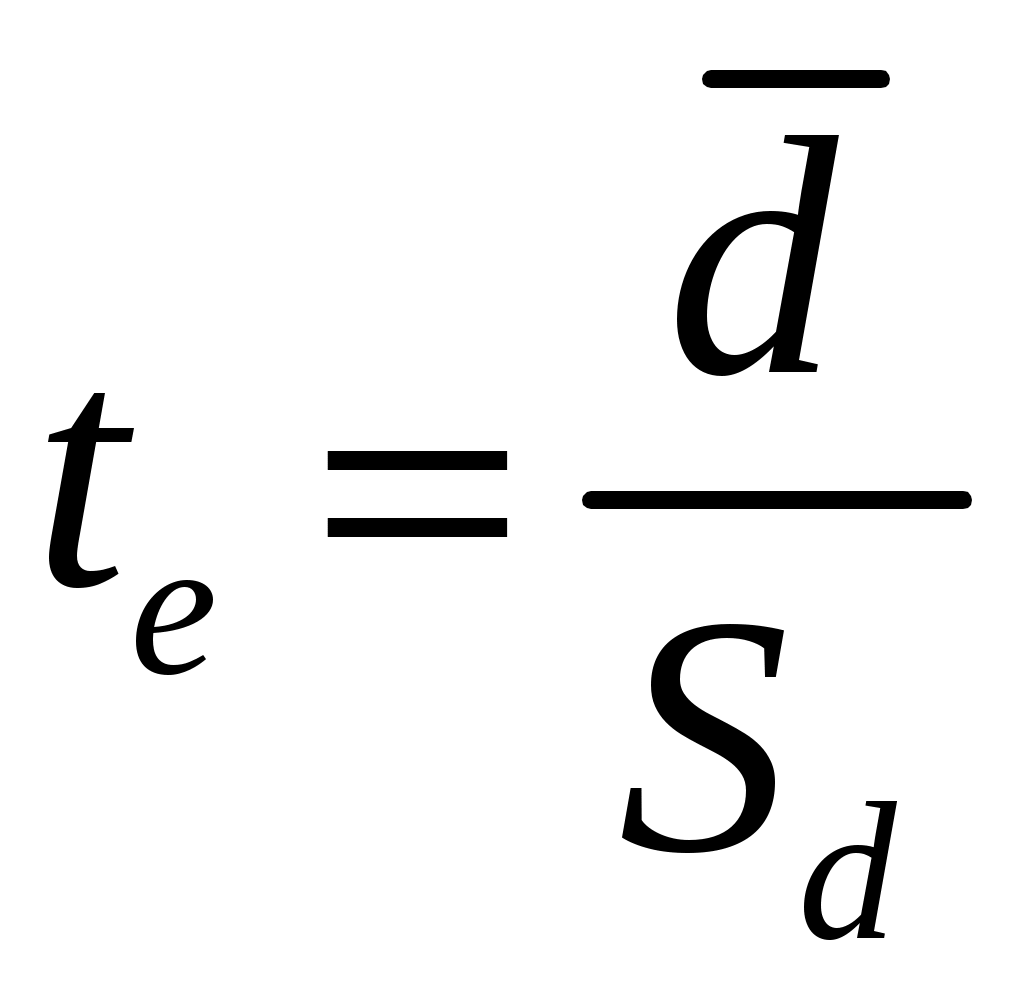где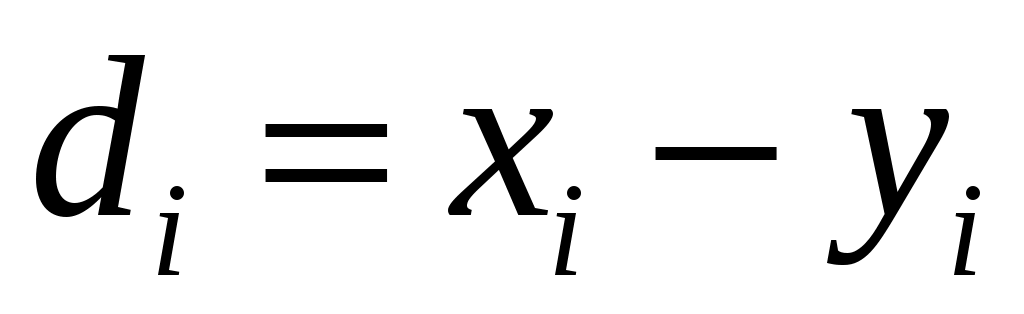
– разности между соответствующими значениями переменной 
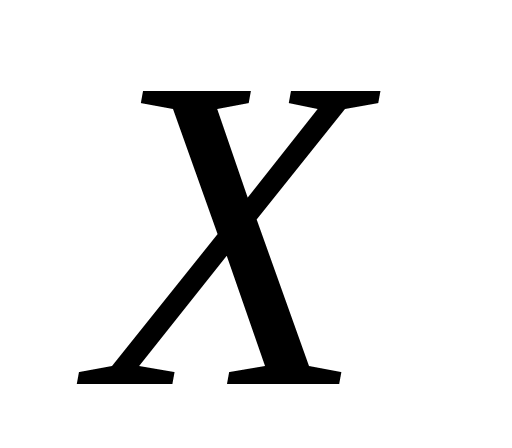и переменной 
; 
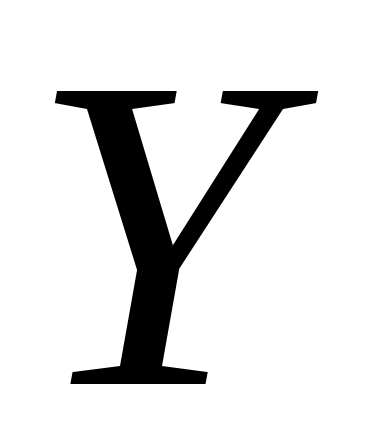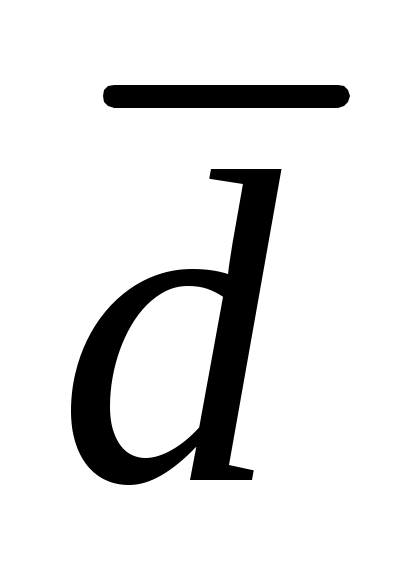– среднее этих разностей; 
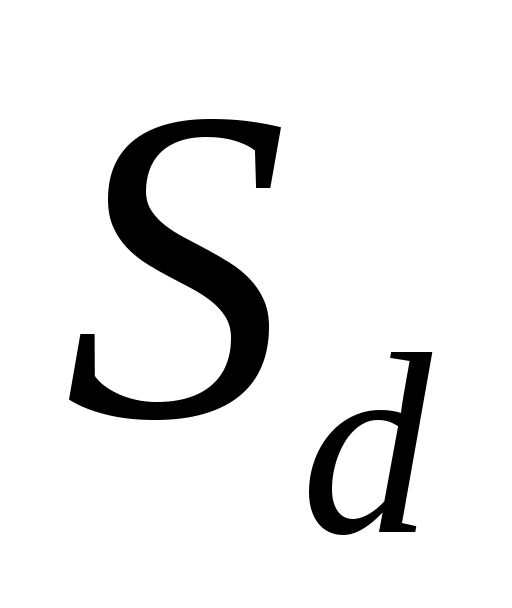вычисляется по следующей формуле:
.
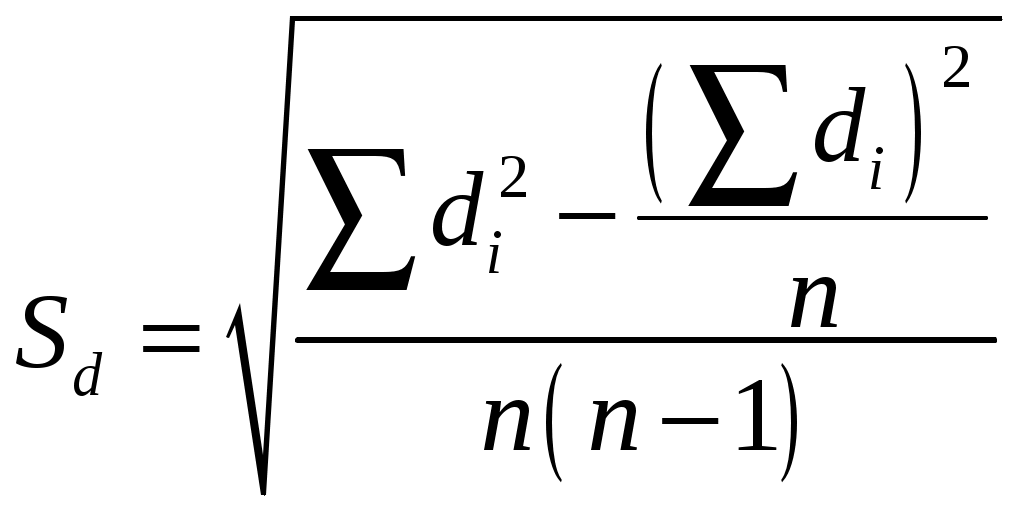Число степеней свободы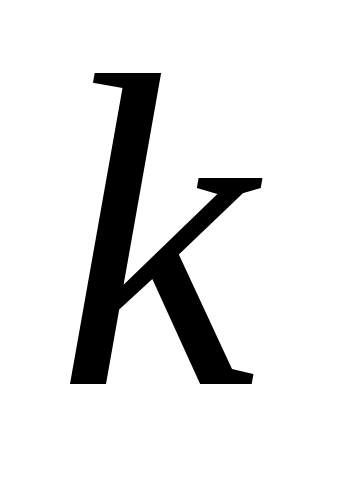
определяется по формуле 
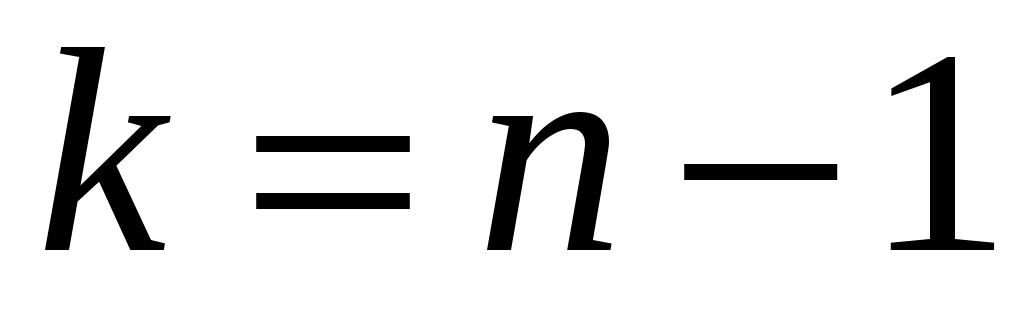. Если 
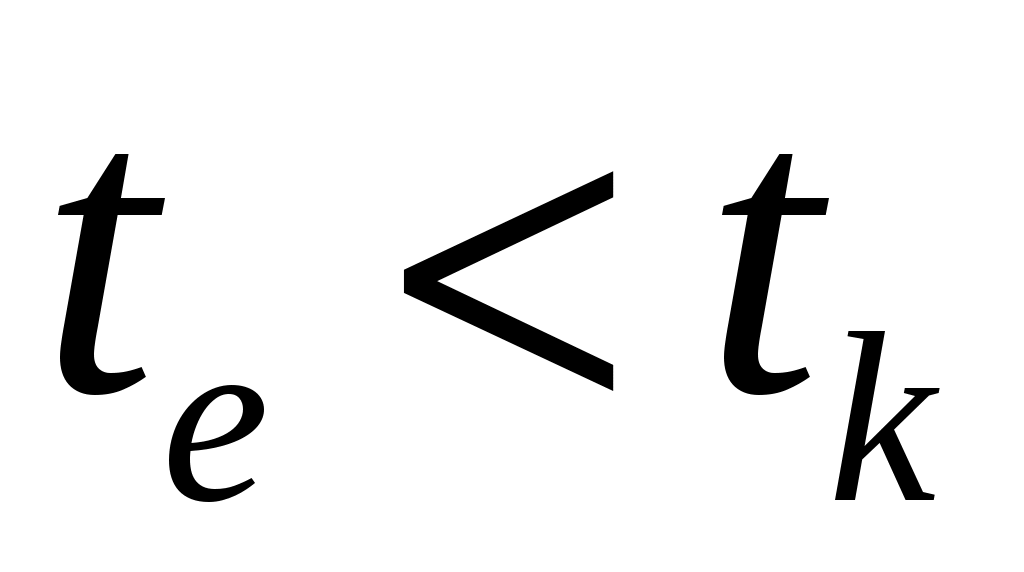, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Выборка
(
)
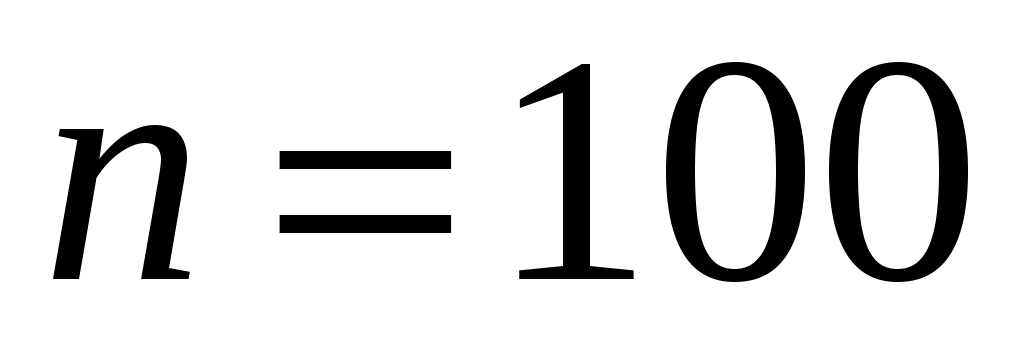Выборка
(
)
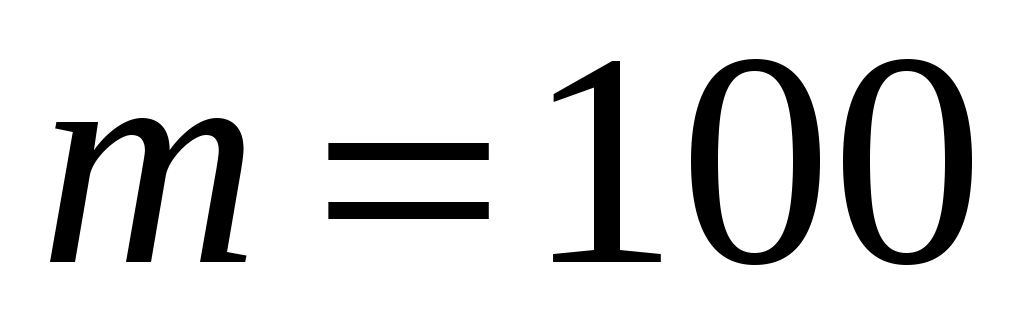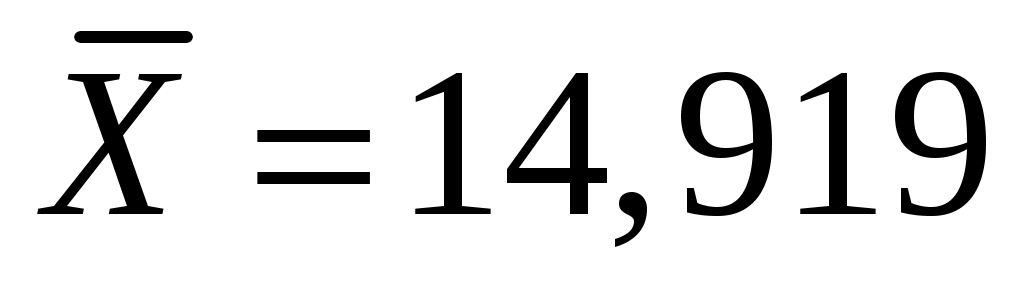
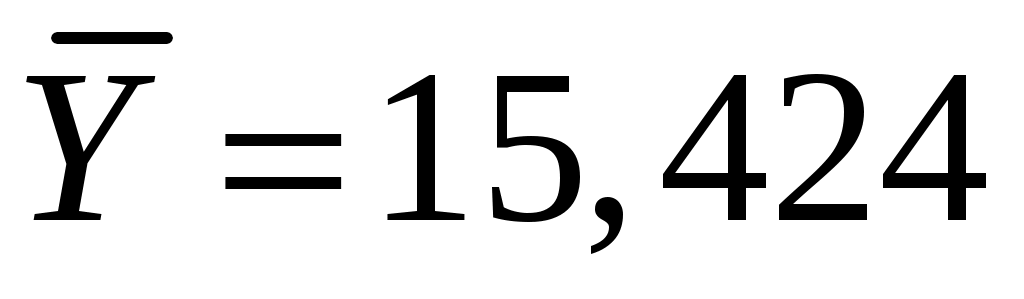
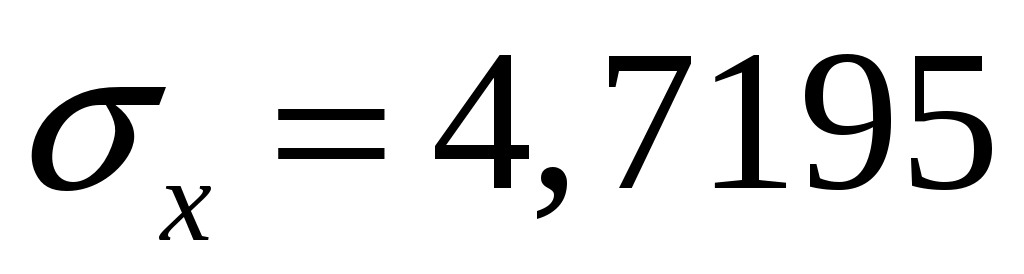
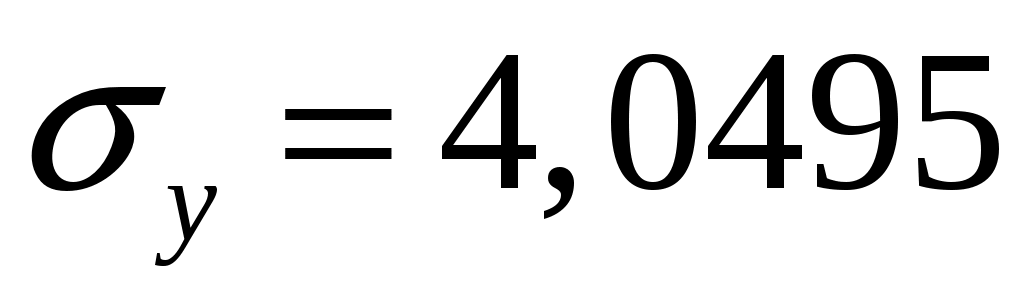
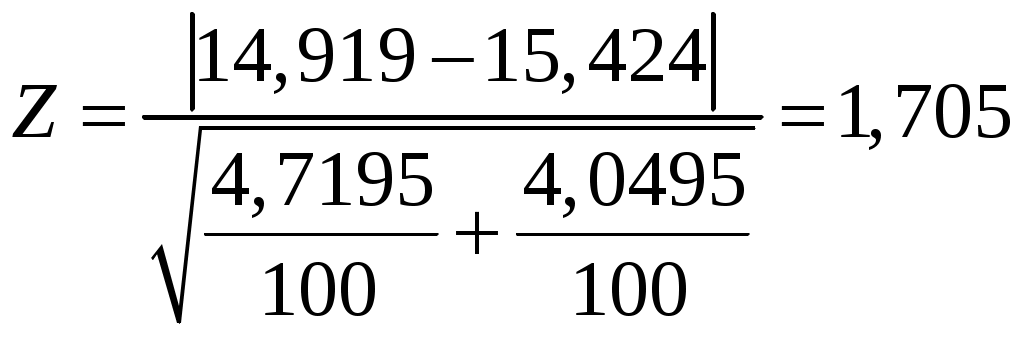
Находим правую критическую точку:
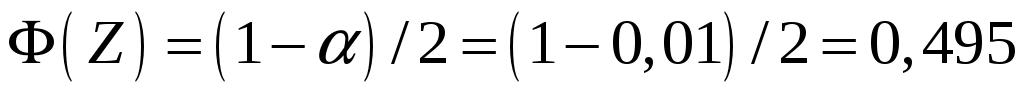
По таблице функции Лапласа находим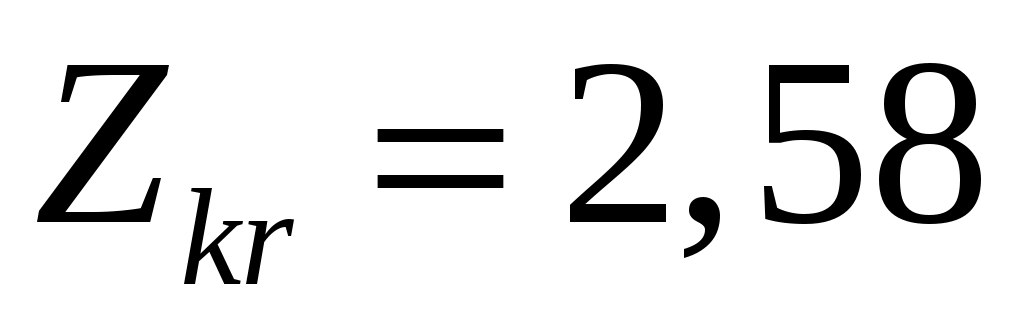
Так как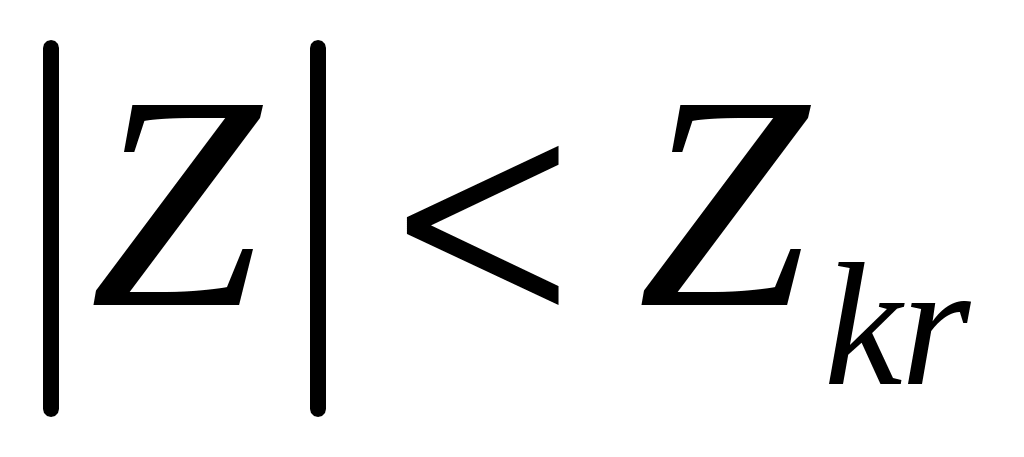
, значит гипотезу о равенстве двух средних выборок принимаем.
Рассмотрим две выборки объемом 100 значений каждая.
Для определения гипотезы о равенстве средних при связанных выборках воспользуемся методом, описанным в теоретической части.
В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.
Вычисление значения t осуществляется по формуле:
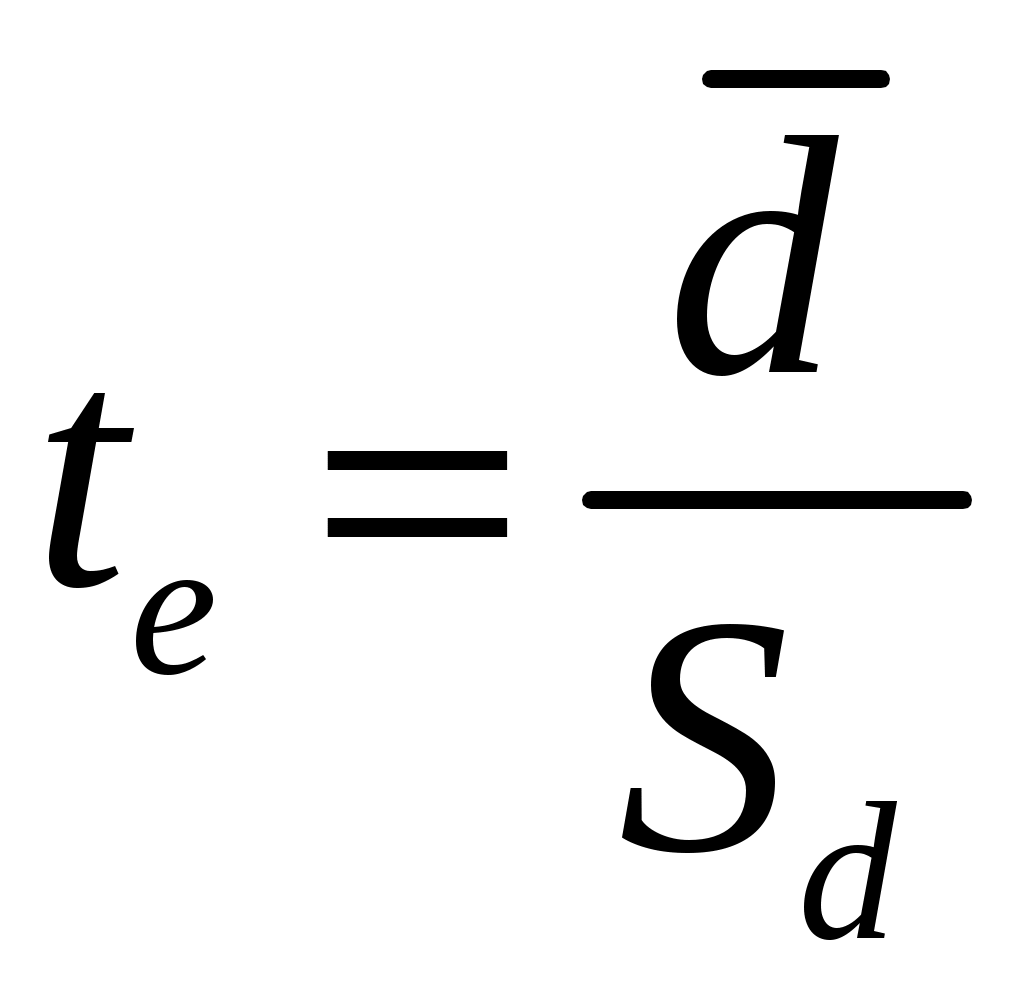,где
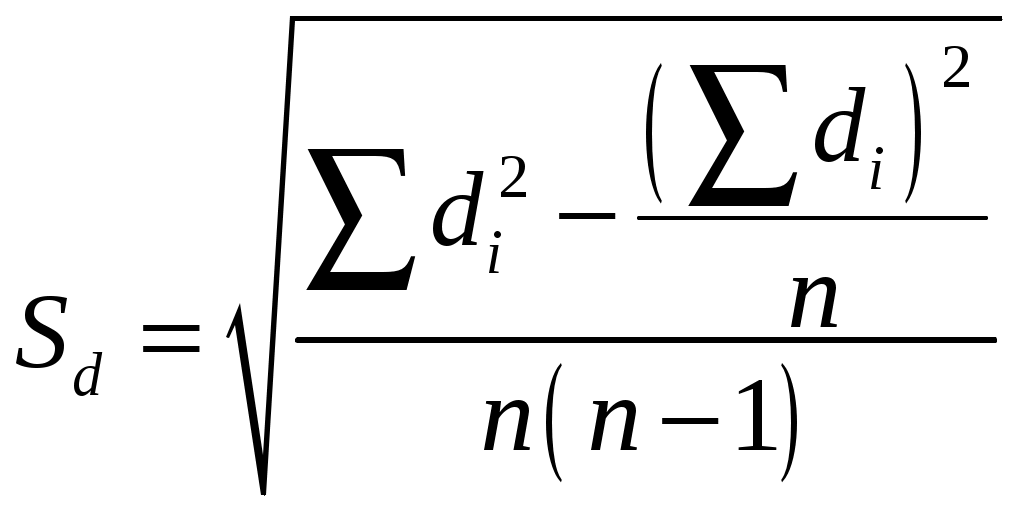– разности между соответствующими значениями переменной и переменной ; – среднее этих разностей; вычисляется по следующей формуле: .Число степеней свободы
определяется по формуле . Если , то нулевая гипотеза принимается, в противном случае принимается альтернативная.2 Практическая часть
2.1 Проверка гипотезы о равенстве средних при равных дисперсиях (на примере двух выборок)
Выборка
( )-
14,4
14,3
12,1
16,4
19,4
12,4
14,3
13,3
15,6
17,9
15,5
17,7
12
13,1
17,6
17,6
14,8
14,3
14,5
15,2
17,4
14,6
14,9
15,3
15
18,5
14
15,1
16,1
15,9
10,6
18,9
14,4
15,3
14,9
14,5
16,7
19,4
13,2
12,9
17,2
19,8
11,5
18,8
11,5
12,8
13,7
13,5
16
16,7
13,6
18,3
9,8
15,1
15,9
11,6
11,8
17,9
16,7
16,2
11,3
16,1
12,4
16,7
15,4
13
16,8
13,7
13,7
12,9
13,5
18,8
16,5
13,2
17,5
10,8
14,8
15,9
17,2
14,4
13,9
14
16,7
12,6
13,3
14,2
16,4
16,2
11,9
13,4
15,3
14,2
12,3
16,4
14,1
14,3
16,5
12,8
16,3
14,1
Выборка
( )-
16,8
14,2
14,2
13,5
16,6
14,8
18
12,8
16,6
15,2
15,2
15,5
16,1
16,8
16,1
14,3
15,4
15,2
13,8
16,2
15,2
18,7
16,6
17,1
15,8
11
16,2
14,2
16,8
15
15,2
16,4
14,8
15,1
12,8
12,8
15
16,1
12,4
19,7
15,8
16,9
14,8
17,5
18,7
16,5
15,4
15,9
17
17,6
18,1
14
10,6
14,8
12,5
14,3
13,3
15,4
14,1
13,3
14
15,9
16
17,2
16,6
15,8
13,5
19,7
16,2
15,6
15
19,4
12,4
16,6
15,5
15,1
15,2
12,4
19,7
15,8
18,7
12,3
10,9
16
11,7
15,6
14,8
17,8
13,3
15
15,2
17,4
20,2
16,5
13,6
19,2
14,7
14,7
13
13,5
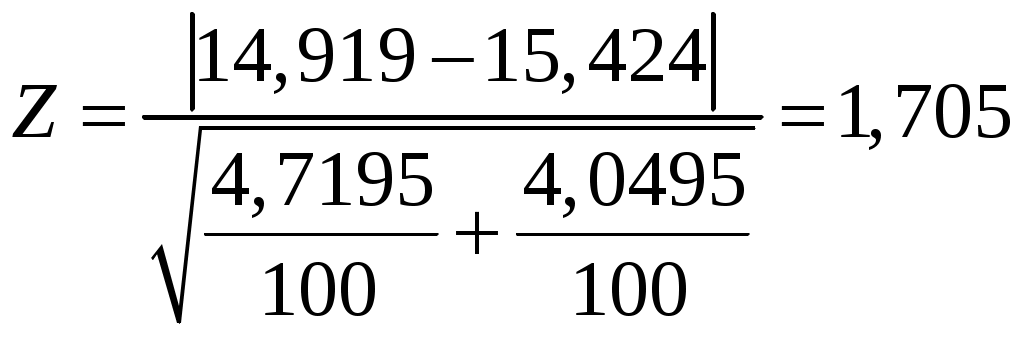
Находим правую критическую точку:
По таблице функции Лапласа находим
Так как
, значит гипотезу о равенстве двух средних выборок принимаем.2.2 Проверка гипотезы о равенстве средних при связанных выборках
Рассмотрим две выборки объемом 100 значений каждая.
Для определения гипотезы о равенстве средних при связанных выборках воспользуемся методом, описанным в теоретической части.
-
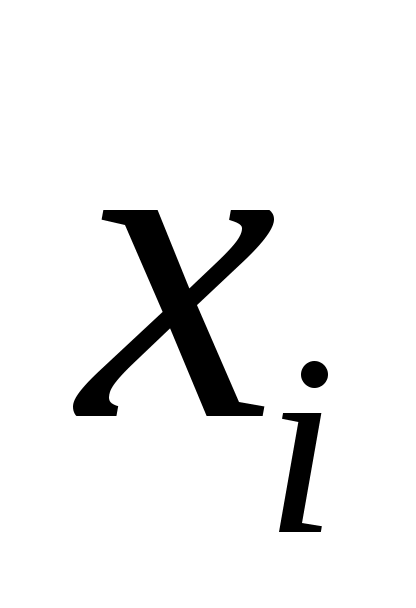
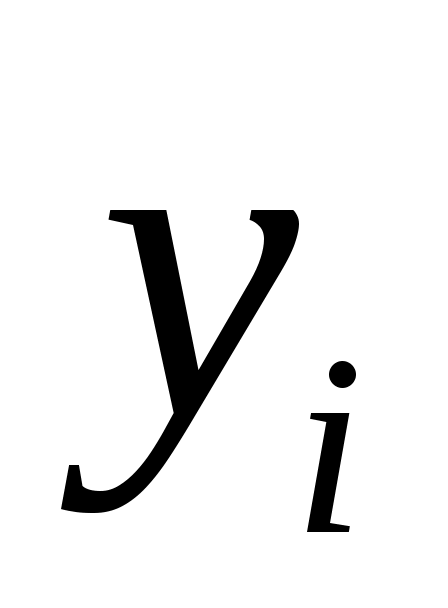
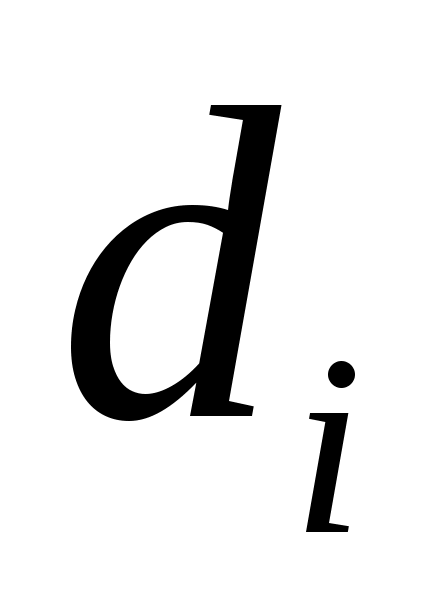
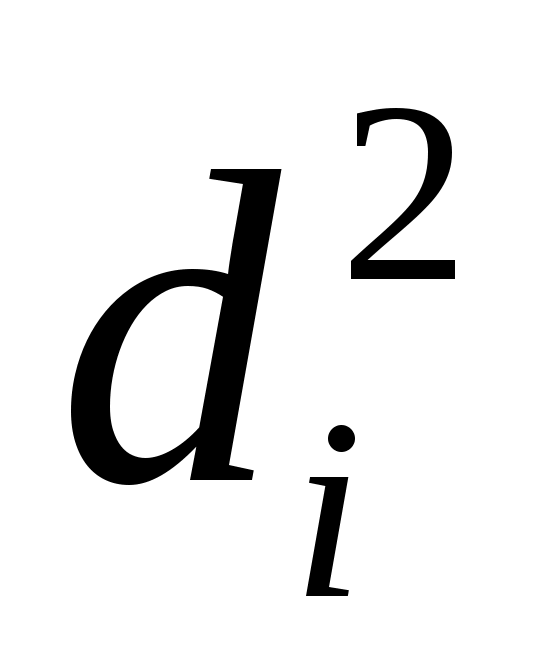
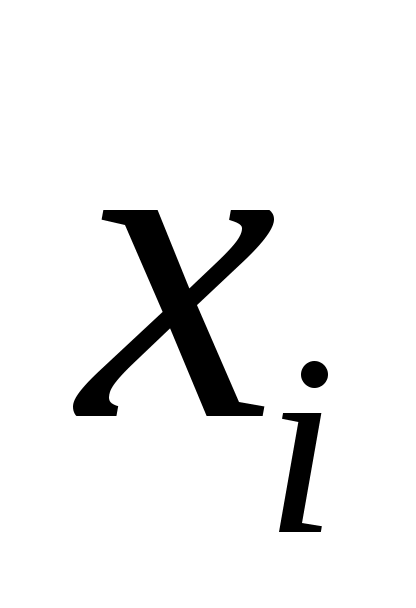
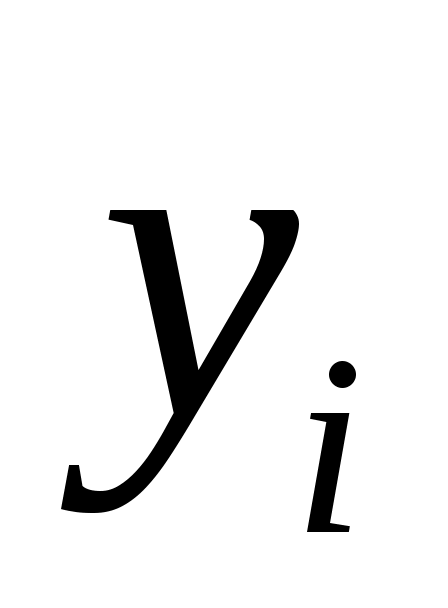
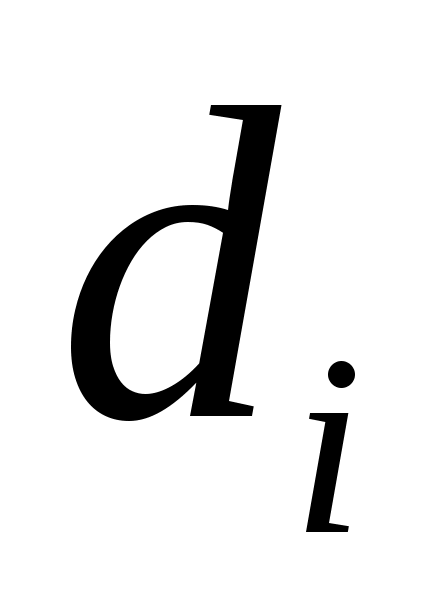
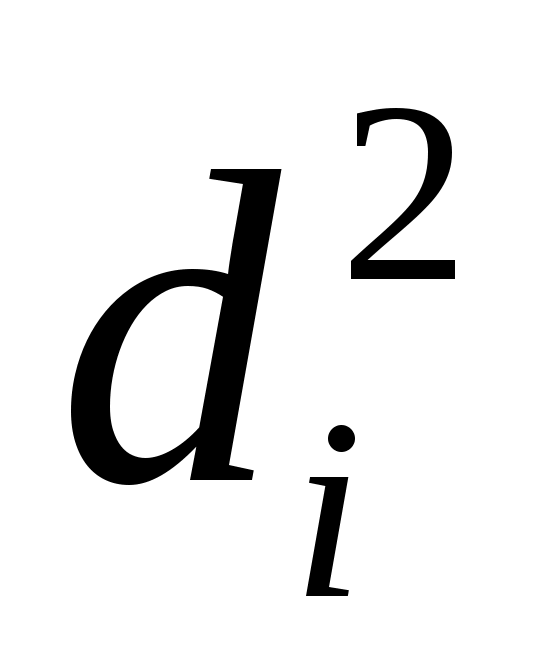
9,8
10,6
0,8
0,64
14,8
15,4
0,6
0,36
10,6
10,9
0,3
0,09
14,9
15,4
0,5
0,25
10,8
11
0,2
0,04
14,9
15,5
0,6
0,36
11,3
11,7
0,4
0,16
15
15,5
0,5
0,25
11,5
12,3
0,8
0,64
15,1
15,6
0,5
0,25
11,5
12,4
0,9
0,81
15,1
15,6
0,5
0,25
11,6
12,4
0,8
0,64
15,2
15,8
0,6
0,36
11,8
12,4
0,6
0,36
15,3
15,8
0,5
0,25
11,9
12,5
0,6
0,36
15,3
15,8
0,5
0,25
12
12,8
0,8
0,64
15,3
15,8
0,5
0,25
12,1
12,8
0,7
0,49
15,4
15,9
0,5
0,25
12,3
12,8
0,5
0,25
15,5
15,9
0,4
0,16
12,4
13
0,6
0,36
15,6
16
0,4
0,16
12,4
13,3
0,9
0,81
15,9
16
0,1
0,01
12,6
13,3
0,7
0,49
15,9
16,1
0,2
0,04
12,8
13,3
0,5
0,25
15,9
16,1
0,2
0,04
12,8
13,5
0,7
0,49
16
16,1
0,1
0,01
12,9
13,5
0,6
0,36
16,1
16,2
0,1
0,01
12,9
13,5
0,6
0,36
16,1
16,2
0,1
0,01
13
13,6
0,6
0,36
16,2
16,2
0
0
13,1
13,8
0,7
0,49
16,2
16,4
0,2
0,04
13,2
14
0,8
0,64
16,3
16,5
0,2
0,04
13,2
14
0,8
0,64
16,4
16,5
0,1
0,01
13,3
14,1
0,8
0,64
16,4
16,6
0,2
0,04
13,3
14,2
0,9
0,81
16,4
16,6
0,2
0,04
13,4
14,2
0,8
0,64
16,5
16,6
0,1
0,01
13,5
14,2
0,7
0,49
16,5
16,6
0,1
0,01
13,5
14,3
0,8
0,64
16,7
16,6
0,1
0,01
13,6
14,3
0,7
0,49
16,7
16,8
0,1
0,01
13,7
14,7
1
1
16,7
16,8
0,1
0,01
13,7
14,7
1
1
16,7
16,8
0,1
0,01
13,7
14,8
1,1
1,21
16,7
16,9
0,2
0,04
13,9
14,8
0,9
0,81
16,8
17
0,2
0,04
14
14,8
0,8
0,64
17,2
17,1
0,1
0,01
14
14,8
0,8
0,64
17,2
17,2
0
0
14,1
14,8
0,7
0,49
17,4
17,4
0
0
14,1
15
0,9
0,81
17,5
17,5
0
0
14,2
15
0,8
0,64
17,6
17,6
0
0
14,2
15
0,8
0,64
17,6
17,8
0,2
0,04
14,3
15
0,7
0,49
17,7
18
0,3
0,09
14,3
15,1
0,8
0,64
17,9
18,1
0,2
0,04
14,3
15,1
0,8
0,64
17,9
18,7
0,8
0,64
14,3
15,2
0,9
0,81
18,3
18,7
0,4
0,16
14,4
15,2
0,8
0,64
18,5
18,7
0,2
0,04
14,4
15,2
0,8
0,64
18,8
19,2
0,4
0,16
14,4
15,2
0,8
0,64
18,8
19,4
0,6
0,36
14,5
15,2
0,7
0,49
18,9
19,7
0,8
0,64
14,5
15,2
0,7
0,49
19,4
19,7
0,3
0,09
14,6
15,2
0,6
0,36
19,4
19,7
0,3
0,09
14,8
15,4
0,6
0,36
19,8
20,2
0,4
0,16